Le Isometrie
Un’isometria è un’affinità tra i punti del piano che conserva le distanze.
In particolare, un’isometria trasforma i segmenti in segmenti di uguale lunghezza, i cerchi in cerchi di uguale raggio, rette perpendicolari in rette perpendicolari, triangoli equilateri in triangoli equilateri di uguale lato, quadrati in quadrati di uguale lato.
L’isometria più semplice è l’identità I, cioè la trasformazione descritta dalle seguenti equazioni:
\[ I: \begin{cases} x’ = x \\ y’ = y \end{cases} \]
In questo caso, quindi, la matrice associata, cioè la matrice dei coefficienti, è data da:
\[ A= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \,\,\,\, \mbox{e} \,\,\,\, \mbox{det}(A) = 1 \]
Le isometrie possono essere di varie tipologie; alcune di esse sono, per esempio, le traslazioni, le rotazioni, le simmetrie rispetto un punto, o una retta, e anche le trasformazioni che si ottengono componendo due o più trasformazioni di questo tipo.
Le traslazioni
Si definisce traslazione di vettore v la corrispondenza biunivoca tra i punti del piano che ad ogni punto P associa il punto P’ tale che:
\[ \overrightarrow{PP’} = \overrightarrow{v} \]
Come abbiamo detto prima, la traslazione è una isometria; consideriamo due punti del piano P e Q, e i loro corrispondenti P’ e Q’, e supponiamo che questi siano generati da una traslazione di vettore v. In questo caso, si ha:
\[\overrightarrow{PP’} = \overrightarrow{v} \]
\[ \overrightarrow{QQ’} = \overrightarrow{v} \]
e la trasformazione preserva le distanze, in quanto i segmenti PQ e P’Q’ sono congruenti.
Notiamo che, se il vettore che descrive la traslazione è diverso dal vettore nullo, cioè:
\[ \overrightarrow{v} \ne \overrightarrow{0} \]
nessun punto può essere mandato in se stesso, tutti subiscono uno spostamento; quindi, possiamo affermare che la trasformazione non ha punti uniti.
Viceversa, se il vettore della trasformazione è proprio il vettore nullo, cioè:
\[ \overrightarrow{v} = \overrightarrow{0} \]
la traslazione è un’identità che fa corrispondere ad ogni punto se stesso.
Formule analitiche
Una traslazione può essere descritta da formula analitiche; in particolare, se un punto P, di coordinate ( x ; y ), viene traslato di un vettore v = ( p ; q ), e il suo corrispondente è il punto P’, di coordinate ( x’ ; y’ ), è possibile determinare le coordinate del nuovo punto mediante le seguenti equazioni:
\[ \tau_{\overrightarrow{v}} : \begin{cases} x’=x+p \\ y’ = y + q \end{cases} \]
dove, la matrice dei coefficienti è:
\[ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \,\,\,\, \mbox{e} \,\,\,\, \mbox{det}(A) = 1 \]
In particolare, possiamo anche determinare le equazioni che descrivono la trasformazione inversa, cioè la traslazione di vettore – v; le equazioni della traslazione inversa sono:
\[ \tau_{-\overrightarrow{v}} : \begin{cases} x’=x-p \\ y’ = y +-q \end{cases} \]
Esempio:
Consideriamo il segmento OP, che ha un estremo nell’origine O(0;0), e l’altro nel punto P (3; 4), e trasliamo il segmento di un vettore v(3; 1).
Per determinare le coordinate degli estremi del segmento traslato, basta sostituire le coordinate dei punti, e il valore del vettore, alle equazioni della traslazione:
\[ \tau_{-\overrightarrow{v}} : \begin{cases} x’=x-p \\ y’ = y +-q \end{cases} \]
ricordando che, nel nostro caso, abbiamo:
\( x_P = 3 \,\,\,\, , \,\,\,\, y_P = 4 \)
\( x_O = 0 \,\,\,\, , \,\,\,\, y_O = 0 \)
\( p = 3 \,\,\,\, , \,\,\,\, q = 1 \)
Determiniamo, quindi, i nuovi punti O’ e P’:

\( O’ : \begin{cases} x’=0+3=3 \\ y’=0+1=1 \end{cases} \rightarrow O'(3;1) \)
\( P’ : \begin{cases} x’=3+3=6 \\ y’=4+1=5 \end{cases} \rightarrow P'(6;5) \)
Composizione di traslazioni
Come abbiamo visto in precedenza, due trasformazioni possono essere composte; in questo caso, consideriamo due traslazioni di vettori, rispettivamente, v e u, tali che:
\[ \tau_{\overrightarrow{v}}: P \rightarrow Q | \overrightarrow{PQ} = \overrightarrow{v} \]
\[ \tau_{\overrightarrow{u}}: Q \rightarrow R | \overrightarrow{QR} = \overrightarrow{u} \]
Notiamo che il punto P viene traslato di vettore v e si trasforma nel punto Q, il quale, poi, viene traslato nel punto R mediante un vettore u; possiamo quindi dire che il punto P viene traslato nel punto R mediante la composizione delle due traslazioni, e possiamo scrivere:
\[ \tau = \tau_{\overrightarrow{u}} \ast \tau_{\overrightarrow{v}} \]
Il vettore che descrive lo spostamento di P in R è dato dalla somma dei vettori u e v.
La composizioni di traslazioni gode d
Potrebbero interessarti
ella proprietà commutativa, in quanto si ha:
\[ \tau = \tau_{\overrightarrow{u}} \ast \tau_{\overrightarrow{v}} = \tau_{\overrightarrow{v}} \ast \tau_{\overrightarrow{u}} \]
Questa proprietà vale perché il vettore che rappresenta lo spostamento di P in R è dato dalla somma dei due vettori u e v, e sappiamo che la somma di vettori gode della proprietà commutativa.





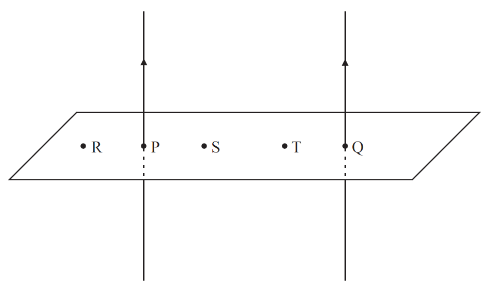 Si abbiano due fili conduttori paralleli percorsi nello stesso verso dalla corrente elettrica d’intensità 1 A e posti alla distanza di 10 cm l’uno dall’altro. Calcolare il modulo del vettore \(\vec{B}\) nei punti R, S, T distanti rispettivamente 3 cm, 3 cm, 7 cm dal punto P, mettendo in evidenza i passaggi matematici necessari a ricavare l’unità di misura dell’induzione magnetica. Disegnare le linee di forza passanti nei punti R, S, T, mettendo in evidenza la direzione e l’orientamento del vettore \(\vec{B}\) negli stessi punti. Ricavare l’espressione matematica che descrive l’andamento del modulo di \(\vec{B}\) tra i punti P e Q e disegnarne il grafico su l piano cartesiano. In ognuno dei punti S e T passa un protone con velocità \(v = 2 \cdot 10^4 m/s\) con la traiettoria parallela ai fili e con verso uguale a quello convenzionale della corrente elettrica. Ricavare il modulo, la direzione e il verso della forza di Lorentz che agisce su ognuno dei due protoni e rappresentarne la traiettoria con un disegno, anche se in maniera approssimata. Si ricorda che il protone ha la stessa carica dell’elettrone, ma con segno positivo (\(1,60 \cdot 10^{-19} C\)).
Si abbiano due fili conduttori paralleli percorsi nello stesso verso dalla corrente elettrica d’intensità 1 A e posti alla distanza di 10 cm l’uno dall’altro. Calcolare il modulo del vettore \(\vec{B}\) nei punti R, S, T distanti rispettivamente 3 cm, 3 cm, 7 cm dal punto P, mettendo in evidenza i passaggi matematici necessari a ricavare l’unità di misura dell’induzione magnetica. Disegnare le linee di forza passanti nei punti R, S, T, mettendo in evidenza la direzione e l’orientamento del vettore \(\vec{B}\) negli stessi punti. Ricavare l’espressione matematica che descrive l’andamento del modulo di \(\vec{B}\) tra i punti P e Q e disegnarne il grafico su l piano cartesiano. In ognuno dei punti S e T passa un protone con velocità \(v = 2 \cdot 10^4 m/s\) con la traiettoria parallela ai fili e con verso uguale a quello convenzionale della corrente elettrica. Ricavare il modulo, la direzione e il verso della forza di Lorentz che agisce su ognuno dei due protoni e rappresentarne la traiettoria con un disegno, anche se in maniera approssimata. Si ricorda che il protone ha la stessa carica dell’elettrone, ma con segno positivo (\(1,60 \cdot 10^{-19} C\)).

 Nel disegno riprodotto qui affianco ed estratto dall’articolo originale, le sue particelle entrano attraverso l’ugello C e, con velocità parallele tra loro, attraversano il campo elettrico e quello magnetico nella regione identificata dalle lettere PLQM. I campi sono paralleli tra di loro e perpendicolari al piano della pagina.
Nel disegno riprodotto qui affianco ed estratto dall’articolo originale, le sue particelle entrano attraverso l’ugello C e, con velocità parallele tra loro, attraversano il campo elettrico e quello magnetico nella regione identificata dalle lettere PLQM. I campi sono paralleli tra di loro e perpendicolari al piano della pagina.

 Nel laboratorio di Fisica, durante una lezione sul magnetismo, scorgi in un angolo un vecchio strumento che avevi utilizzato qualche anno fa per lo studio del moto uniformemente accelerato (Fig. 1): una barretta metallica poggia su due blocchi A e B ancorati ad una guida ad U anch’essa metallica; la guida si trova su un piano perpendicolare al pavimento con il quale è in contatto attraverso due piedini di materiale isolante. La barretta si trova ad un’altezza h dal pavimento e, una volta eliminati i blocchi, scivola verso il basso lungo i binari della guida con attrito trascurabile. Pensando a ciò che hai studiato recentemente ti viene in mente di utilizzare lo strumento per effettuare misure di campi magnetici. Immagini così di immergere completamente lo strumento in un campo magnetico uniforme perpendicolare al piano della guida.
Nel laboratorio di Fisica, durante una lezione sul magnetismo, scorgi in un angolo un vecchio strumento che avevi utilizzato qualche anno fa per lo studio del moto uniformemente accelerato (Fig. 1): una barretta metallica poggia su due blocchi A e B ancorati ad una guida ad U anch’essa metallica; la guida si trova su un piano perpendicolare al pavimento con il quale è in contatto attraverso due piedini di materiale isolante. La barretta si trova ad un’altezza h dal pavimento e, una volta eliminati i blocchi, scivola verso il basso lungo i binari della guida con attrito trascurabile. Pensando a ciò che hai studiato recentemente ti viene in mente di utilizzare lo strumento per effettuare misure di campi magnetici. Immagini così di immergere completamente lo strumento in un campo magnetico uniforme perpendicolare al piano della guida. rappresenta l’andamento nel tempo della velocità della barretta giustificando la scelta fatta .
rappresenta l’andamento nel tempo della velocità della barretta giustificando la scelta fatta .









 Le simmetrie centrali sono isometrie, infatti, se consideriamo due punti qualsiasi del piano, P e Q, e i loro corrispondenti P’ e Q’ nella simmetria di centro C, notiamo che si formano due triangolo congruenti PQC e P’Q’C; in particolare, sono congruenti i lati PQ e P’Q’. Da questo, possiamo dedurre che la trasformazione preserva le distanze, e si tratta quindi di un’isometria.
Le simmetrie centrali sono isometrie, infatti, se consideriamo due punti qualsiasi del piano, P e Q, e i loro corrispondenti P’ e Q’ nella simmetria di centro C, notiamo che si formano due triangolo congruenti PQC e P’Q’C; in particolare, sono congruenti i lati PQ e P’Q’. Da questo, possiamo dedurre che la trasformazione preserva le distanze, e si tratta quindi di un’isometria.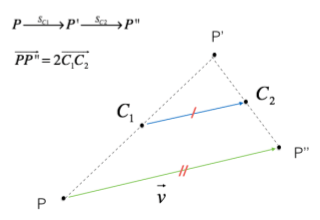 Consideriamo due simmetrie centrali di centro, rispettivamente, $C_1$ e $C_2$; la loro composizione risulta essere la seguente:
Consideriamo due simmetrie centrali di centro, rispettivamente, $C_1$ e $C_2$; la loro composizione risulta essere la seguente: Consideriamo due punti del piano P e Q e una retta $r$; i punti P’ e Q’ sono ottenuti da P e Q tramite una simmetria rispetto alla retta $r$. I triangoli che si formano PHQ e P’H’Q’ sono congruenti, e pertanto hanno i cateti uguali; in particolare, abbiamo che PQ = P’Q’. Possiamo quindi affermare che la simmetria assiale è una isometria, in quanto trasformazione in cui si conservano le distanze.
Consideriamo due punti del piano P e Q e una retta $r$; i punti P’ e Q’ sono ottenuti da P e Q tramite una simmetria rispetto alla retta $r$. I triangoli che si formano PHQ e P’H’Q’ sono congruenti, e pertanto hanno i cateti uguali; in particolare, abbiamo che PQ = P’Q’. Possiamo quindi affermare che la simmetria assiale è una isometria, in quanto trasformazione in cui si conservano le distanze.



