Grafici di funzioni elementari (funzioni esponenziali)

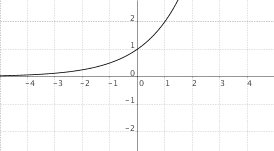
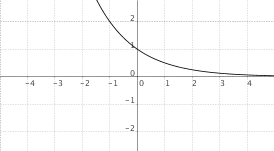
$f(x) = a^x$, $a > 1$	$f(x) = a^{-x}$, $a > 1$
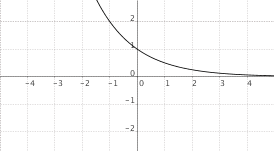
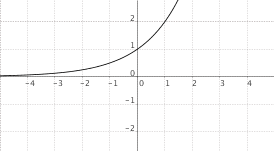
$f(x) = a^x$, $0 < a < 1$	$f(x) = a^{-x}$, $0 < a < 1$
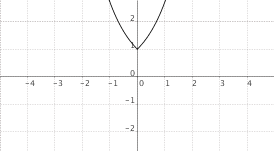
$f(x) = e^{-x^2}$	$f(x) = a^{\|x\|}$, $a > 1$
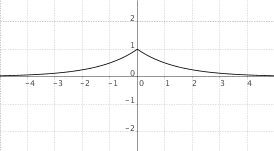
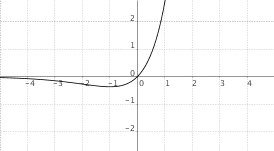
$f(x) = a^{\|x\|}$, $0 < a < 1$	$f(x) = x cdot a^x$, $a > 1$
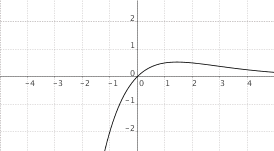
$f(x) = x cdot a^x$, $0 < a < 1$

Grafici di funzioni elementari (funzioni logaritmiche)

$f(x) = log_a(x)$, $a > 1$	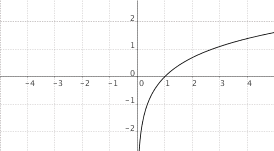$f(x) = log_a(-x)$, $a > 1$
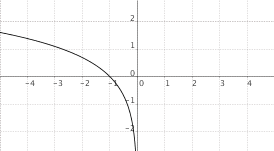$f(x) = log_a(\|x\|)$, $a > 1$	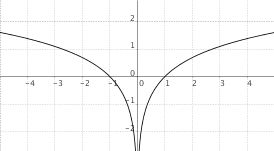$f(x) = log_a(x)$, $0 < a < 1$
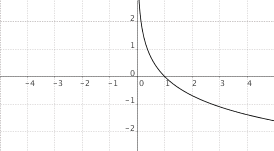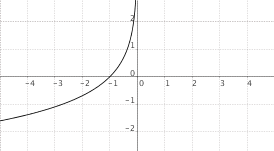
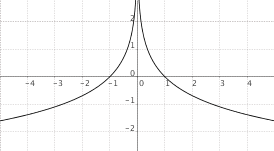
$f(x) = log_a(-x)$, $0 < a < 1$	$f(x) = log_a(\|x\|)$, $0 < a < 1$
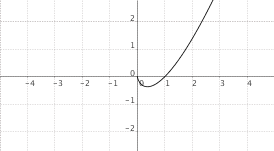
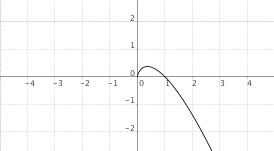
$f(x) = x cdot log_a(x)$, $a > 1$	$f(x) = x cdot log_a(x)$, $0 < a < 1$

Grafici di funzioni elementari (funzioni goniometriche)

$f(x) = sin(x)$	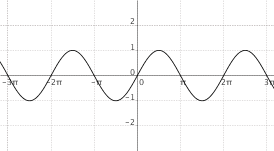$f(x) = cos(x)$
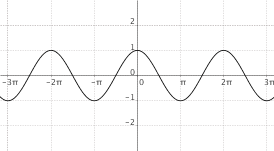$f(x) = "tg"(x)$	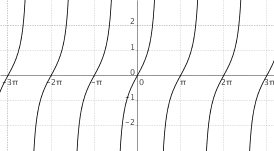$f(x) = "cotg"(x)$
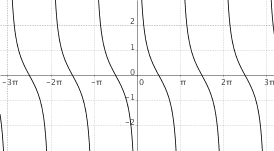$f(x) = "sec"(x)$	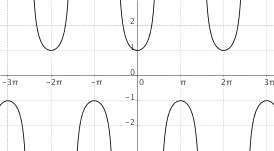$f(x) = "cosec"(x)$
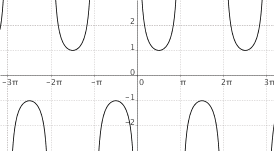$f(x) = "arcsin"(x)$	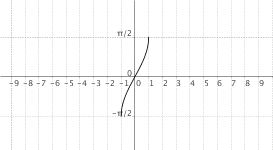$f(x) = "arccos"(x)$
$f(x) = "arctg"(x)$	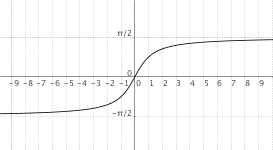$f(x) = "arccotg"(x)$
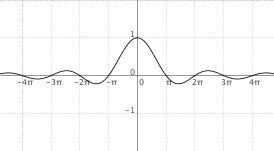
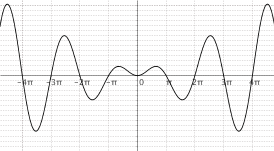
$f(x) = frac{sin(x)}{x}$	$f(x) = x cdot sin(x)$
$f(x) = sin(frac{1}{x})$	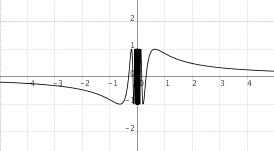$f(x) = x cdot sin(frac{1}{x})$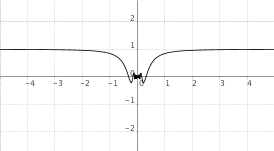
$f(x) = \|sin(x)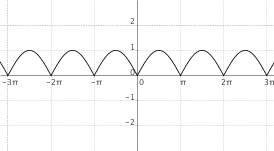\|$	$f(x) = sin(x^2)$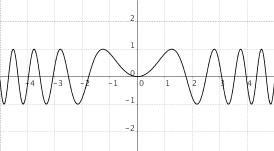

Grafici di funzioni elementari (funzioni iperboliche)

$f(x) = sinh(x)$	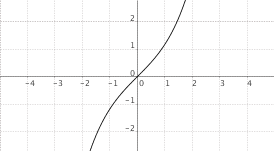$f(x) = cosh(x)$
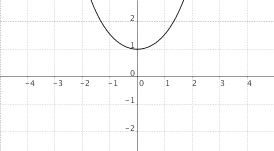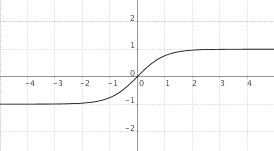
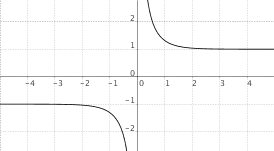
$f(x) = "tgh"(x)$	$f(x) = "cotgh"(x)$
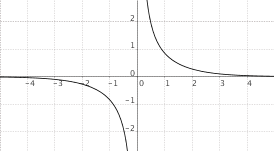
$f(x) = "sech"(x)$	$f(x) = "cosech"(x)$
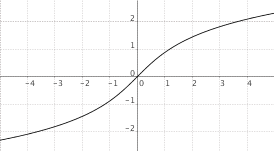
$f(x) = "settsinh"(x)$	$f(x) = "settcosh"(x)$
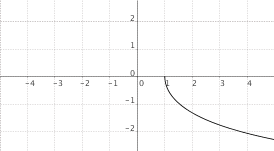$f(x) = "setttgh"(x)$	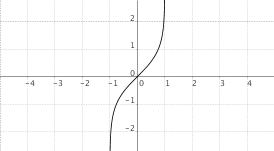$f(x) ="settcotgh"(x)$

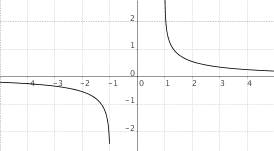Equazioni differenziali ordinarie (EDO)

EDO lineare del I ordine a coefficienti variabili

Un’EDO lineare del I ordine a coefficienti variabili si scrive come

$y’ = \alpha(x) y + \beta(x)$

Detta $A(x)$ una primitiva di $\alpha(x)$, l’integrale generale dell’equazione è

$y(x) = e^{A(x)} [C + \int_{x_0}^{x} e^{- A(s)} \beta(s) ds]$

dove $C$ è una costante arbitraria reale.

Esempio: determinare l’integrale generale dell’equazione $y’ = \cos(x) y + x e^{\sin(x)}$. Risulta $\int \cos(x) dx = \sin(x) + c$, quindi una generica primitiva di $\cos(x)$ è $A(x) = \sin(x)$. Inoltre $\int e^{-\sin(x)} \cdot x \cdot e^{\sin(x)} dx = \int x dx = \frac{x^2}{2} + c$, quindi l’integrale generale dell’equazione differenziale è

$y(x) = e^{\sin(x)} [c + \frac{x^2}{2}]$

EDO lineare omogenea del II ordine a coefficienti costanti (reali)

Un’EDO lineare omogenea del II ordine a coefficienti costanti (reali) si scrive come

$y” + b y’ + c y = 0$, con $b, c \in \mathbb{R}$

– se $b^2 – 4c > 0$, e se $\lambda_1, \lambda_2$ sono le soluzioni (reali) dell’equazione $\lambda^2 + b \lambda + c = 0$, allora l’integrale generale dell’equazione differenziale è

$y(x) = c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x}$, $c_1$ e $c_2$ costanti arbitrarie

– se $b^2 – 4c = 0$, e se $\lambda^{**}$ è la soluzione (doppia) di $\lambda^2 + b \lambda + c = 0$, allora l’integrale generale dell’equazione differenziale è

$y(x) = c_1 e^{\lambda^{**} x} + c_2 x e^{\lambda^{**}}$, $c_1$ e $c_2$ costanti arbitrarie

– se $b^2 – 4 c < 0$, e se $\lambda_1 = \alpha + i \beta$ e $\lambda_2 = \alpha – i \beta$ sono le due soluzioni complesse coniugate di $\lambda^2 + b \lambda + c = 0$, allora l’integrale generale dell’equazione differenziale è

$y(x) = c_1 e^{\alpha x} \cos(\beta x) + c_2 e^{\alpha x} \sin(\beta x)$, $c_1$ e $c_2$ costanti arbitrarie

Esempi

Deteminare l’integrale generale dell’equazione $y” – 3y’ + 2 = 0$. L’equazione $\lambda^2 – 3 \lambda + 2 = 0$ ha come soluzioni $\lambda_1 = 1$ e $\lambda_2 = 2$, pertanto l’integrale generale è

$y(x) = c_1 e^x + c_2 e^{2x}$

Determinare l’integrale generale dell’equazione $y” + 3y’ + \frac{9}{4}y = 0$. L’equazione $\lambda^2 + 3 \lambda + \frac{9}{4} = 0$ ha come soluzione (doppia) $\lambda^{**} = -\frac{3}{2}$, quindi l’integrale generale è

$y(x) = c_1 e^{-\frac{3}{2} x} + c_2 x e^{-\frac{3}{2} x}$

Determinare l’integrale generale dell’equazione $y” + 2 y’ + 8y = 0$. L’equazione $\lambda^2 + 2 \lambda + 8 = 0$ ha come soluzioni $\lambda_1 = -1 + i \sqrt{7}$ e $\lambda_2 = -1 – i \sqrt{7}$, quindi l’integrale generale è

$y(x) = c_1 e^{-x} \cos(\sqrt{7} x) + c_2 e^{-x} \sin(\sqrt{7} x)$

EDO lineare omogenea di ordine $n$ a coefficienti costanti (reali)

Un’EDO lineare omogenea di ordine $n$ a coefficienti costanti (reali) si scrive come

$a_n y^{(n)} + a_{n-1} y^{(n-1)} + \ldots + a_1 y’ + a_0 y = 0$, $a_0, a_1, \ldots, a_n \in \mathbb{R}$ e $a_n \ne 0$

Il polinomio caratteristico associato all’equazione è $p(\lambda) = a_n \lambda^n + a_{n-1} \lambda^{n-1} + \ldots + a_1 \lambda + a_0 = 0$. Il polinomio ha $n$ radici complesse, ognuna contata con la propria molteplicità. Alle $n$ radici sono associate $n$ funzioni linearmente indipendenti che risolvono l’equazione differenziale.

– se $\lambda_i$ è una radice reale con molteplicità $1$, la corrispondente funzione che risolve l’EDO è $y_i(x) = e^{\lambda_i x}$

– se $\lambda_i = \alpha + i \beta$ è una radice complessa, con molteplicità $1$, allora anche $\bar{\lambda_i} = \alpha – i \beta$ è una radice complessa con molteplicità $1$, e le due funzioni relative a tali radici sono $y_{i1}(x) = e^{\alpha x} \cos(\beta x)$ e $y_{i2}(x) = e^{\alpha x} \sin(\beta x)$

– se $\lambda_i$ è una radice reale con molteplicità $k$, allora le $k$ funzioni associate che risolvono l’EDO sono

$y_{i1} = e^{\lambda_i x} \qquad y_{i2} = x e^{\lambda_i x} \qquad \ldots \qquad y_{ik}(x) = x^{k-1} e^{\lambda_i x}$

– se $\lambda_i = \alpha + i \beta$ è una radice complessa con molteplicità $k$, allora anche $\bar{\lambda_i} = \alpha – i \beta$ è una radice complessa con molteplicità $k$, e le $2k$ funzioni associate a tali radici sono

$y_{11}(x) = e^{\alpha x} \cos(\beta x), y_{12}(x) = e^{\alpha x} \sin(\beta x)$

$y_{21}(x) = x e^{\alpha x} \cos(\beta x), y_{22}(x) = x e^{\alpha x} \sin(\beta x)$

$\vdots$

$y_{k1}(x) = x^{k-1} e^{\alpha x} \cos(\beta x), y_{k2}(x) = x^{k-1} e^{\alpha x} \sin(\beta x)$

Con questa casistica si riescono a trovare $n$ soluzioni linearmente indipendenti dell’omogenea, $y_1(x), y_2(x), \ldots, y_n(x)$; l’integrale generale è una combinazione lineare di queste funzioni

$y(x) = c_1 y_1(x) + c_2 y_2(x) + \ldots + c_n y_n(x)$, $c_1, c_2, \ldots, c_n \in \mathbb{R}$

Esempio: determinare l’integrale generale dell’equazione differenziale $y”’ – y” + 4 y’ – 4 = 0$. Il polinomio caratteristico è

$p(\lambda) = \lambda^3 – \lambda^2 + 4 \lambda – 4 = (\lambda – 1) (\lambda^2 + 4)$

Le radici del polinomio caratteristico sono $\lambda_1 = 1$, $\lambda_2 = 2 i$, $\lambda_3 = – 2 i$, e le funzioni associate che risolvono l’omogenea sono

$y_1(x) = e^x \qquad y_2(x) = \cos(2x) \qquad y_3(x) = \sin(2x)$

quindi l’integrale generale cercato è

$y_{"om"}(x) = c_1 e^x + c_2 \cos(2x) + c_3 \sin(2x)$, $c_1, c_2, c_3$ costanti arbitrarie

EDO lineare completa di ordine $n$ a coefficienti costanti (reali)

Un’EDO lineare completa di ordine $n$ a coefficienti costanti (reali) si scrive come

$a_n y^{(n)} + a_{n-1} y^{(n-1)} + \ldots + a_1 y’ + a_0 y = f(x)$, $a_0, a_1, \ldots, a_n \in \mathbb{R}$ e $a_n \ne 0$

Se $y_{"om"}(x)$ è l’integrale generale dell’omogenea associata, e $y_{"p"}$ è una soluzione della completa, allora l’integrale generale della completa è

$y(x) = y_{"om"}(x) + y_{"p"}(x)$

Metodo della variazione delle costanti

Questo metodo serve a trovare una soluzione particolare di una EDO lineare completa di ordine $n$ a coefficienti costanti. Se $y_1(x), y_2(x), \ldots, y_n(x)$ (definite su un intervallo $I \subseteq \mathbb{R}$) sono $n$ soluzioni linearmente indipendenti dell’omogenea, si consideri la matrice

$W(x) = [(y_1(x), \quad y_2(x), \quad \ldots, \quad y_n(x)),(y_1′(x), \quad y_2′(x), \quad \ldots, \quad y_n'(x)),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(y_1^{(n-1)}(x), \quad y_2^{(n-1)}(x), \quad \ldots, \quad y_n^{(n-1)}(x))]$

e il vettore

$F(x) = ((0),(0),(\vdots),(0),(f(x)))$

Poniamo

$C'(x) = ((c_1′(x)),(c_2′(x)),(\vdots),(c_n'(x))) = W^{-1}(x) F(x)$

Fissato $x_0 \in I$, e posto $c_i(x) = \int_{x_0}^x c_i'(x) dx$, per $i = 1, 2, \ldots, n$, una soluzione particolare della completa è

$y_{"p"}(x) = c_1(x) y_1(x) + c_2(x) y_2(x) + \ldots + c_n(x) y_n(x)$

e l’integrale generale della completa è

$y(x) = (c_1(x) + k_1) y_1(x) + (c_2(x) + k_2) y_2(x) + \ldots + (c_n(x) + k_n) y_n(x)$, con $k_1, k_2, \ldots, k_n$ costanti arbitrarie

Esempio: risolvere l’equazione differenziale $y” + y = \frac{1}{\sin(x)}$. L’equazione omogenea è $y” + y = 0$, il polinomio caratteristico è $p(\lambda) = \lambda^2 + 1 = 0$, le cui radici sono $\lambda_{1,2} = \pm i$. Le funzioni associate a tali radici sono $y_1(x) = \cos(x)$ e $y_2(x) = \sin(x)$, e l’integrale generale dell’omogenea è $y_{"om"}(x) = k_1 \cos(x) + k_2 \sin(x)$.

$y_1(x) = \cos(x) \qquad y_1′(x) = -\sin(x)$

$y_2(x) = \sin(x) \qquad y_2′(x) = \cos(x)$

La matrice $W$ e il vettore $F$ risultano pari a

$W(x) = [(\cos(x), \quad \sin(x)),(-\sin(x), \quad \cos(x))] \qquad F(x) = ((0),(\frac{1}{\sin(x)}))$

L’inversa della matrice $W$ è

$W^{-1}(x) = 1 \cdot [(\cos(x), \quad -\sin(x)),(\sin(x), \quad \cos(x))]$

quindi

$W^{-1}(x) F(x) = [(\cos(x), \quad \sin(x)),(-\sin(x), \quad \cos(x))] ((0),(\frac{1}{\sin(x)})) = ((-1),("cotg"(x)))$

$c_1′(x) = -1$, $c_1(x)= \int_{x_0}^x (-1) dx = x_0 – x$

$c_2′(x) = "cotg"(x)$, $c_2(x) = \int_{x_0}^x "cotg"(x) dx = \ln(|\sin(x)|) – \ln(|\sin(x_0)|)$

Quindi una soluzione particolare della completa è

$y_{"p"}(x) = c_1(x) y_1(x) + c_2(x) y_2(x) \implies y_{"p"}(x) = (x_0 – x) \cos(x) + (\ln(|\sin(x)|) – \ln(|\sin(x_0)|)) \sin(x)$

e l’integrale generale della completa è

$y(x) = y_{"om"}(x) + y_{"p"}(x) \implies y(x) = k_1 \cos(x) + k_2 \sin(x) + (x_0 – x) \cos(x) + (\ln(|\sin(x)|) – \ln(|\sin(x_0)|)) \sin(x)$ ($x \in (0, \pi)$ per l’esistenza del logaritmo)

che equivale a

$y(x) = k_1 \cos(x) + k_2 \sin(x) – x \cos(x) + \ln(|\sin(x)|) \sin(x)$

data l’arbitrarietà delle costanti $k_1$ e $k_2$.

Equazione differenziale a variabili separabili

Un’equazione differenziale a variabili separabili è un’equazione differenziale del I ordine del tipo

$y’ = g(x) h(y)$

Le soluzioni si determinano studiando questi due casi:

– tutte le funzioni costanti $y \equiv y_0$, tali che $h(y_0) = 0$, sono soluzioni dell’equazione differenziale

– se $H(y)$ è una primitiva di $\frac{1}{h(y)}$ e $G(x)$ è una primitiva di $g(x)$, le funzioni definite implicitamente da $H(y) = G(x) + C$, al variare di $C \in \mathbb{R}$, sono soluzioni dell’equazione differenziale. In particolare, se $H$ è iniettiva tali funzioni si scrivono come $y(x) = H^{-1}(G(x) + C)$.

Esempio: risolvere l’equazione $y’ = x y^2$. Dato che $y^2 = 0 \implies y = 0$, allora la funzione costante $y \equiv 0$ è soluzione dell’equazione differenziale. Dividendo per $y^2$ si ottiene $\frac{y’}{y^2} = x$, e integrando ambo i membri $\int \frac{y’}{y^2} dx = – \frac{1}{y} + c_1$, $\int x dx = \frac{x^2}{2} + c_2$. Da $-\frac{1}{y} + c_1 = \frac{x^2}{2} + c_2$ segue

$y(x) = \frac{1}{\frac{x^2}{2} + c}$

(dove si è posto $c = c_2 – c_1$) e, assieme alla soluzione costante $y \equiv 0$, rappresenta la soluzione dell’equazione differenziale.

Equazioni riconducibili a variabili separabili

1° caso

$y’ = f(ax + by)$, $a, b \ne 0$

Sostituzione $z(x) = a x + b y(x)$, da cui $z'(x) = a + b y'(x)$, ottenendo

$z’ = a + b f(z)$

che è a variabili separbili con $g(x) = 1$, $h(z) = a + b f(z)$.

Esempio: risolvere l’equazione differenziale $y’ = (x + y)^2 – (x + y) – 1$. Ponendo $z = x + y$, e osservando che $z’ = 1 + y’$, si ottiene

$z’ = 1 + y’ \implies z’ = 1 + (x+y)^2 – (x + y) – 1 \implies $z’ = z^2 – z$

Questa è un’equazione a variabili separabili, le cui soluzioni costanti sono $z \equiv 0$, da cui segue $y = -x$, e $z \equiv 1$ da cui segue $y = 1 – x$. Per trovare le altre soluzioni, si divide ambo i membri per $z^2 – z$, ottenendo

$\frac{z’}{z^2 – z} = 1$

Integrando ambo i membri si trova

$\ln(|1 – \frac{1}{z}|) = x + c \implies |1 – \frac{1}{z}| = e^c \cdot e^x = k \cdot e^x$, con $c \in \mathbb{R}$ e $k \in \mathbb{R}^+$

Togliendo il valore assoluto (visto che $k e^x \ge 0 \quad \forall x \in \mathbb{R}$) e risolvendo rispetto a $z$ si trova $z(x) = \frac{1}{1 – k e^x}$ da cui

$y(x) = \frac{1}{1 – k e^x} – x$

2° caso

$y’ = f(\frac{y}{x})$

Sostituzione $z(x) = \frac{y(x)}{x}$, da cui $x \cdot z(x) = y(x)$ e $z + x z’ = y’$, ottenendo

$z’ = \frac{1}{x} (f(z) – z)$

che è a variabili separabili con $g(x) = \frac{1}{x}$ e $h(z) = f(z) – z$.

Esempio: risolvere dell’equazione $y’ = \frac{4y}{3x} – \frac{8 x^2}{3 y^2}$. Ponendo $z = \frac{y}{x}$, da cui $y = x \cdot z$ e $y’ = z + x \cdot z’$, si ottiene

$y’ = z’ x + z \implies z’ x = y’ -z \implies z’ x = \frac{4}{3} z – \frac{8}{3} z^{-2} – z = \frac{z^3 – 8}{3 z^2}$

da cui

$\frac{3 z^2}{z^3 – 8} z’ = \frac{1}{x}$

L’unica soluzione costante è $z \equiv 2$, a cui corrisponde $y(x) = 2x$. Integrando ambo i membri si ottiene

$\int \frac{1}{x} dx = \ln(|x|) + c_1$,$c_1 \in \mathbb{R}$

$\int \frac{3 z^2}{z^3 – 8} z’ dx = \ln(|z^3 – 8|) + c_2$, $c_2 \in \mathbb{R}$

Posto $c = c_1 – c_2$, uguagliando i risultati, e ricordando che $z = \frac{y}{x}$, si ottiene

$\ln(|\frac{y^3(x)}{x^3} – 8|) = \ln(|x|) + c$

da cui

$|\frac{y^3(x)}{x^3} – 8| = e^{\ln(|x|)} \cdot e^c \implies \frac{y^3(x)}{x^3} – 8 = k \cdot |x| \implies y(x) = x \root{3}{k |x| + 8}$

dove si è posto, per comodità, $k = e^c$.

3° caso

$y’ = f(\frac{a_1 x + b_1 y + c_1}{a_2 x + b_2 y + c_2})$, con $a_1 b_2 \ne a_2 b_1$

Detta $(x_0, y_0)$ la soluzione del sistema

$\{(a_1 x + b_1 y + c_1 = 0),(a_2 x + b_2 y + c_2 = 0):}$

si opera la sostituzione $x = u + x_0$, $y = v + y_0$, da cui $\frac{a_1 x + b_1 y + c_1}{a_2 x + b_2 y + c_2} = \frac{a_1 u + b_1 v}{a_2 u + b_2 v} = \frac{a_1 + b_1 \frac{v}{u}}{a_2 + b_2 \frac{v}{u}}$, ottenendo

$v’ = f(\frac{a_1 + b_1 \frac{v}{u}}{a_2 + b_2 \frac{v}{u}})$

che diventa a variabili separabili con la sostituzione $z(u) = \frac{v(u)}{u}$, come nel caso precedente.

Esempio: risolvere $y’ = \frac{y – x – 2}{y + x}$. Le rette di equazione $y – x – 2 = 0$ e $y + x = 0$ si intersecano nel punto $(x,y) = (-1,1)$, quindi conviene fare la trasformazione

$\{(u = x + 1),(v = y – 1):} \implies \{(x = u – 1),(y = v + 1):}$

$v(u) = y(x) – 1 \implies v(u) = y(u – 1) – 1$, derivando si ottiene $y’ = v’$, da cui

$v’ = \frac{v + 1 – u + 1 – 2}{v + 1 + u – 1} \implies v’ = \frac{v – u}{v + u} \implies v = \frac{\frac{v}{u} – 1}{\frac{v}{u} + 1}$

Ponendo $z(u) = \frac{v(u)}{u}$, da cui $v(u) = u \cdot z(u) \implies v’ = z’ + u z$, si ottiene

$z’ u = v’ – z \implies z’ u = \frac{z-1}{z+1} – z \implies z’ u = \frac{-z^2 – 1}{z+1} \implies \frac{z+1}{z^2 + 1} z’ = -\frac{1}{u}$

Integrando ambo i membri si trova

$\frac{1}{2} \ln(z^2 + 1) + "arctg"(z) = – \ln(|u|) + c$, $c$ costante arbitraria

e ricordando le sostituzioni $z = \frac{v}{u} = \frac{y-1}{x+1}$ si arriva a

$\frac{1}{2} \ln((\frac{y-1}{x+1})^2 + 1) + "arctg"(\frac{y-1}{x+1}) = – \ln(|x+1|) + c$, $c$ costante arbitraria

Tutte le funzioni $y = y(x)$ definite implicitamente dalla relazione precedente soddisfano l’equazione differenziale.

Equazione di Bernoulli

Un’equazione di Bernoulli è un’equazione differenziale del tipo

$y’ = \alpha(x) y + \beta(x) y^s$, con $s \ne 0$ e $s \ne 1$

Sostituzione $z(x) = y^{1-s}(x)$, da cui e $z'(x) = (1 – s) y^{-s}(x) y'(x)$, ottenendo così

$z'(x) = (1 – s) y^{-s}(x) [\alpha(x) y + \beta(x) y^s(x)] \implies z’ = (1 – s) \alpha(x) z + (1 – s) \beta(x)$

che è un’EDO lineare del I ordine a coefficienti variabili.

Esempio: risolvere l’equazione differenziale $y’ = 2 "tg"(x) y + 2 \sqrt{y}$, con $y \ge 0$ e $x \ne \frac{\pi}{2} + k \pi$, $k \in \mathbb{Z}$. Ponendo $z = y^{1 – \frac{1}{2}} = y^{\frac{1}{2}} = \sqrt{y}$ si ottiene $z’ = \frac{1}{2 \sqrt{y}} y’$ e l’equazione diventa

$z’ = \frac{1}{2 \sqrt{y}} [2 "tg"(x) y + 2 \sqrt{y}] \implies z’ = "tg"(x) \sqrt{y} + 1 \implies z’ = "tg"(x) z + 1$

Questa è una EDO del I ordine, con $\alpha(x) = "tg"(x)$, $\beta(x) = 1$. Integrandola con la formula generaleper le EDO lineari del I ordine si trova

$z(x) = \frac{c}{|\cos(x)|} + "tg"(x)$

e ricordando che $y(x) = z^2(x)$ si ottiene

$y(x) = (\frac{C}{|\cos(x)|} + "tg"(x))^2$

EDO a coefficienti variabili notevoli

Equazione di Eulero

L’equazione di Eulero è un’equazione differenziale della forma

$x^2 \cdot y” + a x \cdot y’ + b y = 0$

Con la sostituzione $y(x) = x^r$ si arriva alla seguente equazione in $r$

$r^2 + (a-1)r + b = 0$

Risolta questa equazione, si hanno due possibilità:

– se $r_1 \ne r_2$ l’integrale generale è $y(x) = c_1 x^{r_1} + c_2 x^{r_2}$

– se $r_1 = r_2 = r$ l’integrale generale è $y(x) = (c_1 \ln(x) + c_2) x^r$

Equazione di Legendre

L’equazione di Legendre è un’equazione differenziale della forma

$[(1 – x^2) y’]^’ – 2 x y’ + n (n+1) y = 0$

Le soluzioni sono della forma $y(x) = P_n(x)$, dove i $P_n$ sono i polinomi di Legendre, definiti da

$P_n(x) = \frac{1}{2^n \cdot n!} \frac{d^n}{d x^n} ((x^2 – 1)^n)$

Equazione di Laguerre

L’equazione di Laguerre è un’equazione differenziale del tipo

$x y” + (1-x) y’ + n y = 0$

Soluzioni di questa equazione sono le funzioni $y(x) = L_n(x)$, dove $L_n$ sono i polinomi di Laguerre, definiti da

$L_n(x) = \frac{e^x}{n!} \frac{d^n}{d x^n} (x^n e^{-x})$

Equazione di Laguerre associata

Le equazioni di Laguerre associate sono equazioni del tipo

$y” + (\frac{m+1}{x} – 1) y’ + (\frac{n + \frac{1}{2} (m+1)}{x}) y = 0$

Soluzioni di questa equazione sono i polinomi associati di Laguerre $L_n^m(x)$, definiti da

$L_n^m(x) = \frac{(-1)^m \cdot n!}{(n-m)!} e^{-x} x^{-m} \frac{d^{n-m}}{d x^{n-m}} (e^{-x} x^n)$

Equazione di Bessel

L’equazione di Bessel è un’equazione differenziale della forma

$x^2 y” + x y’ + (x^2 – \nu^2) y = 0$

Si chiamano funzioni di Bessel del primo tipo le funzioni definite da

$J_{\nu}(x) = x^{\nu} \sum_{m=0}^{+\infty} \frac{(-1)^m x^{2m}}{2^{2m + \nu} \cdot m! \cdot \Gamma(\nu + m + 1)}$

dove $\Gamma(x) = \int_0^{+\infty} t^{x-1} e^{-t} dt$ è la Gamma di Eulero, e vale $\Gamma(n + 1) = n!$ per ogni $n \in \mathbb{N}$. Quindi per $\nu = n \in \mathbb{N}$ le funzioni di Bessel del primo tipo diventano

$J_{n}(x) = x^{n} \sum_{m=0}^{+\infty} \frac{(-1)^m x^{2m}}{2^{2m + n} \cdot m! \cdot (n + m)}$

e vale $J_{-n}(x) = (-1)^n J_n(x)$, per ogni $n \in \mathbb{N}$.

Si chiamano funzioni di Bessel del secondo tipo le funzioni definite da

$Y_{\nu}(x) = \frac{J_{\nu}(x) \cos(\nu \pi) – J_{-\nu}(x)}{\sin(\nu \pi)}$

e vale $Y_n(x) = \lim_{\nu \to n} Y_{\nu}(x)$.

– Se $\nu \in \mathbb{Z}$ la soluzione dell’equazione di Bessel è data da $y(x) = a J_{\nu}(x) + b J_{\nu}(x)$.

– La soluzione generale dell’equazione di Bessel è data da $y(x) = a J_{\nu}(x) + b Y_{\nu}(x)$

Equazione di Bessel modificata

L’equazione di Bessel modificata è un’equazione differenziale della forma

$x^2 y” + x y’ – (x^2 + \nu^2) y = 0$

Le soluzioni sono date dalle funzioni di Bessel modificate

$I_{\nu}(x) = i^{-\nu} J_{\nu}(ix)$

$K_{\nu} = \frac{\pi [I_{-\nu}(x) – I_{\nu}(x)]}{2 \sin(\nu \pi)}$

Equazione di Hermite

Le equazioni di Hermite sono equazioni differenziali del tipo

$y” – 2xy’ + 2ny = 0$ e $z” – x z’ + n z = 0$

Soluzioni di queste equazioni sono i polinomi di Hermite, definiti da

$y(x) = "H"_n(x) = (-1)^n e^{\frac{x^2}{2}} \frac{d^n}{d x^n} (e^{-\frac{x^2}{2}}) = 2^{\frac{n}{2}} "He"_n(x \sqrt{2})$ (soluzione della prima equazione)

$z(x) = "He"_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} (e^{-x^2}) = 2^{-\frac{n}{2}} "H"_n(\frac{x}{\sqrt{2}})$ (soluzione della seconda equazione)

Equazioni di Chebyshev

Le equazioni di Chebyshev sono di due tipi, quelle del primo tipo sono della forma

$(1 – x^2) y” – 3 x y’ + n (n+2) y = 0$

le cui soluzioni sono

$y(x) = U_n(x) = \frac{\sin[(n+1) "arccos"(x)]}{\sqrt{1 – x^2}}$

Le equazioni del secondo tipo hanno invece la forma

$(1 – x^2) y” – x y’ + n^2 y = 0$

e le soluzioni sono

$y(x) = T_n(x) = \cos(n \cdot "arccos"(x))$

Equazioni di Weber

Le equazioni di Weber sono equazioni differenziali del tipo

$y” + (n + \frac{1}{2} – \frac{1}{4} x^2) y = 0$

Le soluzioni sono date da

$y(x) = W_n(x) = "He"_n(x) e^(-\frac{x^2}{4})$

Trasformata di Laplace

Definizione

Data $f: \mathbb{R} \to \mathbb{R}$, con $f(t) = 0$ per ogni $t < 0$, si chiama trasformata di Laplace (monolatera) di $f$, e si indica con $\mathcal{L}[f](s)$, la funzione definita da

$\mathcal{L}[f](s) = \int_0^{+\infty} f(t) e^{-st} dt$

dove $s \in \mathbb{C}$, purché tale integrale esista finito. L’insieme degli $s \in \mathbb{C}$ tali che l’integrale precedente esiste finito si chiama regione di convergenza. Se per un certo $\alpha \in \mathbb{R}$ l’integrale

$\int_0^{+\infty} |f(t)| e^{-\alpha t} dt$

converge, allora la trasformata di $f$ è definita per $s = \alpha + i \beta$, per ogni $\beta \in \mathbb{R}$, e la $f$ si dice trasformabile.

Ascissa di convergenza: data $f$, se esistono $\alpha, M, t_0 \in \mathbb{R}^+$, tali che $|f(t)| \le M \cdot e^{\alpha t}$, per ogni $t > t_0$, allora $\mathcal{L}[f](s)$ esiste nel semipiano complesso $"Re"(s) > \alpha$, e $\alpha$ si dice ascissa di convergenza.

Proprietà della trasformata di Laplace

Linearità

$\mathcal{L}[a f(t) + b g(t)](s) = a \mathcal{L}[f(t)](s) + b \mathcal{L}[g(t)](s)$, per ogni $a, b \in \mathbb{R}$

Trasformata della derivata

$\mathcal{L}[f'(t)](s) = s \mathcal{L}[f(t)](s) – f(0)$

$\mathcal{L}[f”(t)](s) = s^2 \mathcal{L}[f(t)](s) – s f(0) – f'(0)$

$\mathcal{L}[f^{(n)}(t)](s) = s^n \mathcal{L}[f(t)](s) – s^{n-1} f(0) – s^{n-2} f'(0) – \ldots – f^{n-1}(0)$

Trasformata dell’integrale

$\mathcal{L}[\int_0^t f(u) du](s) = \frac{1}{s} \mathcal{L}[f(t)](s)$

Moltiplicazione per $t$

$\mathcal{L}[t \cdot f(t)](s) = – \frac{d}{ds} \mathcal{L}[f(t)](s)$

Divisione per $t$

$\mathcal{L}[\frac{f(t)}{t}](s) = \int_s^{+\infty} \mathcal{L}[f(t)](u) du$

Traslazione complessa

Se $\mathcal{L}[f(t)](s) = F(s)$, allora

$\mathcal{L}[e^{at} f(t)](s) = F(s-a)$

Traslazione nel tempo

Detta $H(t)$ la funzione di Heaviside, risulta

$\mathcal{L}[f(t-a) H(t-a)](s) = e^{-as} \mathcal{L}[f(t)](s)$

Moltiplicazione per $t^n$

$\mathcal{L}[t^n f(t)](s) = (-1)^n \frac{d^n}{d s^n} (\mathcal{L}[f(t)](s))$

Prodotto di convoluzione

La trasformata di un prodotto di convoluzione equivale al prodotto ordinario delle trasformate, cioè

$\mathcal{L}[(f \otimes g)(t)](s) = \mathcal{L}[f(t)](s) \cdot \mathcal{L}[g(t)](s)$

dove $(f \otimes g)(t) = \int_0^t f(\tau) g(t – \tau) d \tau$ denota il prodotto di convoluzione.

Trasformata di una funzione periodica

Se $f$ è una funzione periodica di periodo $T$, allora

$\mathcal{L}[f(t)](s) = \frac{1}{1 – e^{-sT}} \mathcal{L}[f_t(t)](s)$

dove $f_t(t)$ è la funzione troncata sul periodo, cioè $f_t(t) = f(t)$ se $t \in [0, T]$, e $f_t(t) = 0$ altrimenti.

Teorema del valore finale

Se $\lim_{t \to +\infty} f(t)$ e $\lim_{s \to 0} s F(s)$ esistono finiti, allora

$\lim_{t \to +\infty} f(t) = \lim_{s \to 0} s F(s)$

Tavola delle principali trasformate di Laplace

Funzione	Trasformata
$\delta(t)$ (delta di Dirac)	$1$
$H(t) = \{(1, \quad "se " t \ge 0),(0, \quad "se " t < 0):}$ (funzione di Heaviside)	$\frac{1}{s}$
$t \cdot H(t)$ (rampa unitaria)	$\frac{1}{s^2}$
$H(t-a)$ (funzione di Heaviside traslata)	$\frac{1}{s} e^{-as}$
$e^{at} H(t)$	$\frac{1}{s-a}$
$t^n \cdot H(t)$	$\frac{n!}{s^{n+1}}$
$\root{n}{t} \cdot H(t)$	$s^{-(1 + \frac{1}{n})} \Gamma(1 + \frac{1}{n})$ ($\Gamma$ indica la Gamma di Eulero)
$\frac{t^{n-1}}{(n-1)!} e^{at} H(t)$ (esponenziale polinomiale)	$\frac{1}{(s-a)^n}$
$\sin(\omega t) H(t)$	$\frac{\omega}{s^2 + \omega^2}$
$\cos(\omega t) H(t)$	$\frac{s}{s^" + \omega^2}$
$\sinh(\omega t) H(t)$	$\frac{\omega}{s^2 – \omega^2}$
$\cosh(\omega t) H(t)$	$\frac{s}{s^2 – \omega^2}$
$\ln(t)$	$-\frac{\ln(s) + \gamma}{s}$, dove $\gamma$ è la costante di Eulero-Mascheroni
$\frac{1}{\omega_n \sqrt{1 – \zeta^2}} e^{-\zeta \omega_n t} \sin(\omega_n \sqrt{1 – \zeta^2} t) H(t)$	$\frac{1}{s^2 + 2 \zeta \omega_n s + \omega_n^2}$ (fattore trinomio)
$e^{-at} \cos(\omega t) H(t)$	$\frac{s+a}{(s+a)^2 + \omega^2}$
$e^{-at} \sin(\omega t) H(t)$	$\frac{\omega}{(s+a)^2 + \omega^2}$
$J_n(t)$ (funzione di Bessel di prima specie)	$\frac{(s + \sqrt{s^2 + 1})^{-n}}{s^2 + 1}$
$I_n(t)$ (funzione di Bessel modificata di prima specie)	$\frac{(s + \sqrt{s^2 – 1})^{-n}}{s^2 – 1}$

Antitrasformata di Laplace

Se $F(s)$ è una trasformata di Laplace con regione di convergenza $\Omega$, allora la sua antitrasformata vale

$f(t) = \lim_{\beta \to +\infty} \frac{1}{2 \pi i} \int_{\alpha – i \beta}^{\alpha + i \beta} F(s) e^{s t} ds$

dove la retta verticale $s = \alpha + i \beta$ nel piano complesso è interna alla regione di convergenza $\Omega$.

Antitrasformata di Laplace di funzioni razionali

Data una trasformata di Laplace razionale della forma $F(s) = \frac{\beta_{n-1} s^{n-1} + \ldots + \beta_1 s + \beta_0}{s^n + \alpha_{n-1} s^{n-1} + \ldots + \alpha_1 s + \alpha_0}$, dove gli $\alpha_i$ e $\beta_i$ sono coefficienti reali, per calcolare la rispettiva antitrasformata si possono seguire i seguenti passi

1) Per prima cosa si fattorizza il denominatore, mediante il calcolo delle sue radici, e si scrive la trasformata in questa forma

$F(s) = \frac{\beta_{n-1} s^{n-1} + \ldots + \beta_1 s + \beta_0}{\prod_{j=1}^{r} (s – p_j)^{q_j} \cdot \prod_{j=r+1}^{c} (s – p_j)^{q_j} (s – \bar{p}_j)^{q_j}}$

dove

– $p_j$, con $j = 1, 2, \ldots, r$ sono le radici reali del denominatore

– $p_j = \sigma_j + i \omega_j$, con $j = r+1, r+2, \ldots, c$ e $\omega_j > 0$ sono radici complesse del denominatore

– $\bar{p}_j$, $j = r+1, r+2, \ldots, c$ sono le radici del denominatore complesse coniugate di $p_j$

– $q_j$, $j = 1, 2, \ldots, c$, sono le molteplicità algebriche delle radici

2) Fatto questo si scompone la $F(s)$ in fratti semplici, in questo modo

$F(s) = \sum_{j=1}^{r} \sum_{h=1}^{q_j} \frac{R_{jh}}{(s – p_j)^h} + \sum_{j=r+1}^c \sum_{h=1}^{q_j} (\frac{R_{jh}}{(s – p_j)^h} + \frac{\bar{R}_{jh}}{(s – \bar{p}_j)^h})$

dove $R_{jh}$ è il residuo dato da

$R_{jh} = \lim_{s \to p_j} \frac{1}{(q_j – h)!} \frac{d^{q_j – h}}{ds^{q_j – h}} ((s – p_j)^{q_j} F(s))$

per ogni $j = 1, 2, \ldots, c$ e per ogni $h = 1, 2, \ldots, q_j$

3) Per ultima cosa si antitrasforma $F(s)$ usando le trasformate e le proprietà notevoli

$f(t) = \{(\sum_{j=1}^{r} \sum_{h=1}^{q_j} R_{jh} \frac{t^{h-1}}{(h-1)!} e^{p_j t} + \sum_{j=r+1}^c \sum_{h=1}^{q_j} (R_{jh} \frac{t^{h-1}}{(h-1)!} e^{p_j t} + \bar{R}_{jh} \frac{t^{h-1}}{(h-1)!} e^{\bar{p}_j t}), \quad "se " t \ge 0),(0, \quad "se " t < 0):}$

e osservando che $e^{i x} + e^{- i x} = 2 \cos(x)$, $\forall x \in \mathbb{R}$, l’antitrasformata può essere scritta come

$f(t) = \{(\sum_{j=1}^{r} \sum_{h=1}^{q_j} R_{jh} \frac{t^{h-1}}{(h-1)!} e^{p_j t} + \sum_{j=r+1}^c \sum_{h=1}^{q_j} 2 M_{jh} \frac{t^{h-1}}{(h-1)!} e^{\sigma_j t} \cos(\omega_j t + \theta_{jh}), \quad "se " t \ge 0),(0, \quad "se " t < 0):}$

dove $\sigma_j$ è la parte reale di $p_j$, $\omega_j$ è la parte immaginaria di $p_j$, $M_{jh}$ è il modulo di $R_{jh}$, $\theta_{jh}$ è la fase di $R_{jh}$.

Esempio: antitrasformare la funzione $F(s) = \frac{1}{(s+1)(s-2)}$. La funzione $F$ è razionale, e si può scomporre in fratti semplici come $F(s) = \frac{A}{s+1} + \frac{B}{s-2}$, dove

$A = \lim_{s \to -1} (s+1) \frac{1}{(s+1)(s-2)} = – \frac{1}{3} \qquad B = \lim_{s \to 2} (s – 2) \frac{1}{(s+1)(s-2)} = \frac{1}{3}$

quindi $F(s) = -\frac{1}{3} \frac{1}{s+1} + \frac{1}{3} \frac{1}{s-2}$, e sfruttando la tavola delle trasformate notevoli e la linearità della trasformata di Laplace si trova

$f(t) = – \frac{1}{3} e^{-t} H(t) + \frac{1}{3} e^{2t} H(t)$

Trasformata zeta

Definizione

Data una successione $f_k$, $k = 0, 1, 2, \ldots$, si chiama trasformata zeta di $f_k$, e si indica con $Z[f_k](z)$ o $F(z)$, la funzione

$F(z) = \sum_{k=0}^{+\infty} f_k z^{-k}$

definita per $z \in \Omega \subseteq \mathbb{C}$. L’insieme $\Omega$ si chiama regione di convergenza, ed è formato da tutti gli $z \in \mathbb{C}$ tali per cui la serie precedente risulta convergente.

Proprietà

Nel seguito, per comodità, si indicheranno con $F(z)$ e $G(z)$ le trasformate zeta di, rispettivamente, $f_k$ e $g_k$.

Linearità

$Z[a f_k + b g_k](z) = a F(z) + b G(z)$, per ogni $a, b \in \mathbb{R}$

Proprietà del ritardo (scorrimento verso destra)

$Z[f_{k – h}](z) = z^{-h} F(z)$, per ogni $h \in \mathbb{N}$

Proprietà dell’anticipo (scorrimento verso sinistra)

$Z[f_{k+1}](z) = z F(z) – z f_0$

$Z[f_{k+2}](z) = z^2 F(z) – z^2 f_0 – z f_1$

$\vdots$

$Z[f_{k+h}](z) = z^h F(z) – z^h f_0 – z^{h-1} f_1 – \ldots – z f_{h-1}$, per ogni $h \in \mathbb{N} \setminus \{0\}$

Caso particolare: se $f_0 = f_1 = \ldots = f_{h-1} = 0$, allora $Z[f_{k + h}](z) = z^h F(z)$

Traslazione nel dominio di $z$

$Z[a^k f_k](z) = F(\frac{z}{a})$, $a \ne 0$

Trasformata della somma di convoluzione

$Z[\sum_{j=0}^{k} f_{k-j} g_j] = F(z) G(z)$

Moltiplicazione per $k$

$Z[k \cdot f_k](z) = – z \frac{d}{dz} F(z)$

Teorema del valore finale

Se $\lim_{k \to +\infty} f_k$ e $\lim_{z \to 1} \frac{z-1}{z} F(z)$ esistono finiti, allora

$\lim_{k \to +\infty} f_k = \lim_{z \to 1} \frac{z-1}{z} F(z)$

Trasformate zeta notevoli

Successione	Trasformata
$\delta_k^0 = \{(1, \quad "se " k = 0),(0, \quad "altrimenti"):}$ (impulso unitario)	$1$
$\delta_k^1 = u_k = \{(1, \quad "se " k = 0", " 1", " 2", " \ldots),(0, \quad "altrimenti"):}$ (gradino unitario)	$\frac{z}{z-1}$
$k u_k$ (rampa unitaria)$	$\frac{z}{(z-1)^2}$
$u_{k-h}$ (gradino unitario con inizio in $k=h$)	$z^{-h} \frac{z}{z-1}$
$a^k u_k$ (successione esponenziale)	$\frac{z}{z-a}$
$k \cdot a^k \cdot u_k$	$\frac{a z}{(z-a)^2}$
$a^k ((k),(h))$ (potenza-polinomio)	$\frac{a^h z}{(z-a)^{h+1}}$
$\sin(k \theta) \cdot u_k$ (sinusoide)	$\frac{z \sin(\theta)}{z^2 – 2 z \cos(\theta) + 1}$
$\cos(k \theta) \cdot u_k$	$\frac{z^2 – z \cos(\theta)}{z^2 – 2 z \cos(\theta) + 1}$

Antitrasformata zeta

Data una trasformata zeta razionale $F(z)$, per risalire alla corrispondente successione $f_k$ si possono seguire i seguenti passi

1) Definire $\bar{F}(z) = \frac{1}{z} F(z)$

2) Scomporre $\bar{F}(z)$ in fratti semplici

3) Considerare che $F(z) = z \bar{F}(z)$

4) Antitrasformare $F(z)$ facendo uso delle trasformate notevoli

Esempio: antitrasformare $F(z) = \frac{1}{(z-1)(z+2)}$. Risulta $\bar{F}(z) = \frac{1}{z} F(z) = \frac{1}{z(z-1)(z+2)}$. Scomponendo in fratti semplici si ottiene $\bar{F}(z) = \frac{A}{z} + \frac{B}{z-1} + \frac{C}{z+2}$ dove

$A = \lim_{z \to 0} z \bar{F}(z) = \lim_{z \to 0} z \frac{1}{z(z-1)(z+2)} = \frac{1}{2} \qquad B = \lim_{z \to 1} (z-1) F(z) = \lim_{z \to 1} (z-1) \frac{1}{z(z-1)(z+2)} = \frac{1}{3}$

$C = \lim_{z \to -2} (z+2) \bar{F}(z) = \lim_{z \to -2} (z+2) \frac{1}{z(z-1)(z+2)} = \frac{1}{6}$

Quindi $\bar{F}(z) = -\frac{1}{2} \frac{1}{z} + \frac{1}{3} \frac{1}{z-1} + \frac{1}{6} \frac{1}{z+2}$, di conseguenza $F(z) = -\frac{1}{2} + \frac{1}{3} \frac{z}{z-1} + \frac{1}{6} \frac{z}{z+2}$, e antitrasformando, sfruttando le trasformate notevoli, si ottiene

$f_k = -\frac{1}{2} \delta_k^0 + (\frac{1}{3} + \frac{1}{6} (-2)^k) u_k$

Serie di Fourier

Serie di Fourier in forma di esponenziali complessi

Se $f: \mathbb{R} \to \mathbb{R}$ è una funzione periodica di periodo $T$ a quadrato sommabile sul periodo, cioè $\int_0^T (f(x))^2 dx < \infty$, allora si può sviluppare in serie di Fourier mediante esponenziali complessi, nel seguente modo

$f(x) = \sum_{n=-\infty}^{+\infty} c_n e^{i \frac{2 \pi}{T} n x}$

dove

$c_0 = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) dx$ è il valor medio

e in generale

$c_n = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) e^{- i \frac{2 \pi}{T} n x} dx$

Nota: se $x_0$ è un punto di discontinuità di salto, allora $\sum_{n=-\infty}^{+\infty} c_n e^{i \frac{2 \pi}{T} n x_0} = \frac{f(x_0^+) + f(x_0^-)}{2}$. Questo vuol dire che nei punti di discontinuità di salto la serie di Fourier converge alla metà del salto.

Serie di Fourier trigonometrica

$f(x) =\frac{a_0}{2} + \sum_{n=1}^{+\infty} (a_n \cos(\frac{2 \pi}{T} n x) + b_n \sin(\frac{2 \pi}{T} n x))$

dove

$a_0 = \frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) dx$

e in generale

$a_n = \frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \cos(\frac{2 \pi}{T} n x) dx$

$b_n = \frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \sin(\frac{2 \pi}{T} n x) dx$

Identità di Parseval

Se $f: \mathbb{R} \to \mathbb{R}$ è una funzione $T$-periodica, a quadrato sommabile sul periodo, e $f(x) =\frac{a_0}{2} + \sum_{n=1}^{+\infty} (a_n \cos(\frac{2 \pi}{T} n x) + b_n \sin(\frac{2 \pi}{T} n x))$ è il suo sviluppo in serie di Fourier, allora vale l’identità di Parseval

$\frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} (f(x))^2 dx = \frac{a_0^2}{2} + \sum_{n=1}^{+\infty} (a_n^2 + b_n^2)$

Caso particolare: funzioni $2 \pi$-periodiche

Per $f: \mathbb{R} \to \mathbb{R}$ periodiche di periodo $2 \pi$ e a quadrato sommabile sul periodo, le serie di Fourier, in forma complessa e trigonometrica, assumono la seguente forma.

Serie di Fourier complessa

$f(x) = \sum_{n=-\infty}^{+\infty} c_n e^{i n x}$

con

$c_0 = \frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) dx$

$c_n = \frac{1}{2 \pi} \int_{-\pi}^{\pi} f(x) e^{- i n x} dx$

Serie di Fourier in forma trigonometrica

$f(x) =\frac{a_0}{2} + \sum_{n=1}^{+\infty} (a_n \cos(n x) + b_n \sin(n x))$

con

$a_0 = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) dx$

$a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(n x) dx$

$b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(n x) dx$

Identità di Parseval

$\frac{1}{\pi} \int_{-\pi}^{\pi} (f(x))^2 dx = \frac{a_0^2}{2} + \sum_{n=1}^{+\infty} (a_n^2 + b_n^2)$

Trasformata di Fourier

Definizione

Sia $g: \mathbb{R} \to \mathbb{C}$ una funzione complessa di variabile reale, se

$\int_{-\infty}^{+\infty} g(t) e^{-i 2 \pi f t} dt$

converge la $g$ si dice trasformabile secondo Fourier. In tal caso il risultato dell’integrale si chiama trasformata di Fourier di $g$, e si scrive $\mathcal{F}[g(t)](f) = \int_{-\infty}^{+\infty} g(t) e^{-i 2 \pi f t} dt$.

Condizioni sufficienti per la trasformabilità secondo Fourier

1) Se $g: \mathbb{R} \to \mathbb{C}$ è una funzione a quadrato sommabile, cioè $\int_{-\infty}^{+\infty} |g(t)|^2 dt < \infty$, allora $g$ è trasformabile secondo Fourier.

2) Criterio di Dirichlet:

– se $g: \mathbb{R} \to \mathbb{R}$ è una funzione a modulo sommabile, cioè $\int_{-\infty}^{+\infty} |g(t)| dt < \infty$

– se in qualunque intervallo chiuso e limitato $[a,b]$ la funzione $g$ ha un numero finito di discontinuità di salto

– se in qualunque intervallo chiuso e limitato $[a,b]$ la funzione $g$ ha un numero finito di massimi e minimi

allora la funzione $g$ è trasformabile secondo Fourier.

Antitrasformata di Fourier

Se $G(f) = \mathcal{F}[g(t)](f)$, allora $g(t)$ è l’antitrasformata di $G(f)$, e vale

$g(t) = \int_{-\infty}^{+\infty} G(f) e^{i 2 \pi f t} df$

Proprietà della trasformata di Fourier

Per semplicità notazionale, si indicherà con $G(f)$ e $H(f)$ le trasformate di Fourier di, rispettivamente, $g(t)$ e $h(t)$.

Simmetrie: trasformata di una funzione reale

Se $g(t)$ è una funzione reale, e $G(f)$ è la sua trasformata di Fourier, allora

$"Re"(G(f)) = \int_{-\infty}^{+\infty} g(t) \cos(2 \pi f t) dt \qquad "Im"(G(f)) = -\int_{-\infty}^{+\infty} g(t) \sin(2 \pi f t) dt$

e inoltre

$"Re"(G(f)) = "Re"(G(-f))$ (la parte reale della trasformata è una funzione pari)

$"Im"(G(f)) = – "Im"(G(f))$ (la parte immaginaria della trasformata è una funzione dispari)

che equivalgono a

$G(f) = \bar{G(-f)}$ (la trasformata è una funzione complessa a simmetria hermitiana)

Dette $M(f)$ e $\theta(f)$ il modulo e la fase di $G(f)$, rispettivamente, risulta

$M(-f) = M(f)$ (il modulo è una funzione pari)

$\theta(-f) = – \theta(f)$ (la fase è una funzione dispari)

Simmetrie: trasformata di una funzione reale pari

Se $g(t)$ è una funzione reale pari, e $G(f)$ è la sua trasformata di Fourier, allora

$"Re"(G(f)) = 2 \int_{0}^{+\infty} g(t) \cos(2 \pi f t) dt \qquad "Im"(G(f)) = 0$

Quindi la trasformata di una funzione reale pari è una funzione reale pari.

Simmetrie: trasformata di una funzione reale dispari

Se $g(t)$ è una funzione reale dispari, e $G(f)$ è la sua trasformata di Fourier, allora

$"Re"(G(f)) = 0 \qquad "Im"(G(f)) = -2 \int_{0}^{+\infty} g(t) \sin(2 \pi f t) dt$

Quindi la trasformata di una funzione reale pari è una funzione immaginaria pura, e $"Im"(G(f))$ è una funzione dispari.

Linearità

$\mathcal{F}[\alpha g(t) + \beta h(t)](f) = \alpha G(f) + \beta H(f)$, per ogni $\alpha, \beta \in \mathbb{R}$

Inversione degli assi

Se la trasformata di Fourier di $g(t)$ è $G(f)$, allora la trasformata di Fourier di $g(-t)$ è $G(-f)$

Coniugazione complessa

Se la trasformata di Fourier di $g(t)$ è $G(f)$, allora la trasformata di Fourier di $\bar{g(t)}$ (complesso coniugato di $g(t)$) è $\bar{G(-f)}$.

Teorema del valore finale

Se $g(t)$ è una funzione reale, e $G(f)$ è la sua trasformata di Fourier, allora

$\int_{-\infty}^{+\infty} g(t) dt = G(0)$

Proprietà di dualità

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora la trasformata di Fourier di $G(t)$ è $g(-f)$.

Proprietà del ritardo

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora

$\mathcal{F}[g(t – t_0)](f) = G(f) e^{-i 2 \pi f t_0}$, per ogni $t_0 \in \mathbb{R}$

Traslazione in $f$

Se la trasformata di Fourier di $g(t)$ è $G(f)$, allora

$\mathcal{F}[g(t) e^{i 2 \pi f_0 t}](f) = G(f – f_0)$

Proprietà del cambiamento di scala

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora

$\mathcal{F}[g(\alpha t)](f) = \frac{1}{|\alpha|} G(\frac{f}{\alpha})$, per ogni $\alpha \in \mathbb{R} \setminus \{0\}$

Proprietà della modulazione

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora

$\mathcal{F}[g(t) \cos(2 \pi f_0 t)](f) = \frac{G(f – f_0) + G(f + f_0)}{2}$, per ogni $f_0 \in \mathbb{R}$

$\mathcal{F}[g(t) \sin(2 \pi f_0 t)](f) = \frac{G(f – f_0) – G(f + f_0)}{2i}$, per ogni $f_0 \in \mathbb{R}$

Proprietà della derivata

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora

$\mathcal{F}[\frac{d}{dt} g(t)](f) = i 2 \pi f \cdot G(f)$

Proprietà dell’integrale

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora

$\mathcal{F}[\int_{-\infty}^t g(u) du](f) = \frac{1}{i 2 \pi f} G(f) + \frac{\delta(f)}{2} G(0)$

Trasformata del prodotto

La trasformata di Fourier del prodotto ordinario di due funzioni è uguale al prodotto di convoluzione delle trasformate. Se $G(f)$ e $H(f)$ sono le trasformate di Fourier di $g(t)$ e $h(t)$, rispettivamente, allora

$\mathcal{F}[g(t) h(t)](f) = G(f) \otimes H(f) = \int_{-\infty}^{+\infty} G(\nu) H(f – \nu) d \nu$

Traformata del prodotto di convoluzione

La trasformata di Fourier del prodotto di convoluzione di due funzioni equivale al prodotto ordinario delle trasformate. Se $G(f)$ e $H(f)$ sono le trasformate di Fourier di $g(t)$ e $h(t)$, rispettivamente, allora

$\mathcal{F}[g(t) \otimes h(t)](f) = \mathcal{F}[\int_{-\infty}^{+\infty} g(\tau) h(t – \tau) d \tau](f) = G(f) H(f)$

Teorema di Parseval

Se $G(f)$ è la trasformata di Fourier di $g(t)$, allora

$\int_{-\infty}^{+\infty} |g(t)|^2 dt = \int_{-\infty}^{+\infty} |G(f)|^2 df$

Trasformata di una funzione periodica

Se $g(t)$ è una funzione periodica di periodo $T$, e $G_t(f)$ è la trasformata di Fourier della funzione $g_t(t)$ troncata sul periodo (cioè $g_t(t) = g(t)$ se $t \in [0,T]$ e $g_t(t) = 0$ se $t \notin [0, T]$), allora

$\mathcal{F}[g(t)](f) = \frac{1}{T} \sum_{k= -\infty}^{+\infty} G_t(\frac{k}{T}) e^{i \frac{2 \pi k t}{T}}$ (formula di Poisson)

Come si può vedere la formula di Poisson rende evidente il legame fra serie e trasformata di Fourier.

Trasformate di Fourier notevoli

funzione	trasformata
$1$	$\delta(f)$ (delta di Dirac)
$c$ (costante)	$c \cdot \delta(f)$
$u(t) = \{(1, \quad "se " t > 0),(\frac{1}{2}, \quad "se " t = 0),(0, "se " t < 0):}$	$\frac{1}{i 2 \pi f} + \frac{\delta(f)}{2}$
$t \cdot u(t)$	$\frac{1}{(i 2 \pi f)^2} + \frac{\delta(f)}{i 4 \pi f}$
$t^n \cdot u(t)$	$\frac{n!}{(i 2 \pi f)^{n+1}} + \frac{\delta(f) \cdot n!}{2 (i 2 \pi f)^n}$
$t$	$\frac{i}{2 \pi} \frac{d}{df} \delta(f)$
$\|t\|$	$-\frac{1}{2 \pi^2 f^2}$
$\|t^n\|$ ($n$ dispari)	$\frac{2 n!}{(i 2 \pi f)^{n+1}}$
$"sgn"(t)$ (funzione segno)	$\frac{1}{i 2 \pi f}$
$\delta(t)$	$1$
$"rect"(t) = \{(1, \quad "se " \|t\| < \frac{1}{2}),(\frac{1}{2}, \quad "se " \|t\| = \frac{1}{2}),(0, \quad "altrimenti"):}$	$"sinc"(f) = \{(\frac{\sin(\pi f)}{\pi f}, \quad "se " f \ne 0),(1, \quad "se " f = 0):}$
$"sinc"(t)$	$"rect"(f)$
$"tr"(t) = \{(1 – \|t\|, \quad "se " \|t\| < 1),(0, \quad "altrimenti"):}$	$"sinc"^2(f)$
$"sinc"^2(t)$	$"tr"(f)$
$\frac{1}{t}$	$-i \pi "sgn"(f)$
$\frac{1}{t^n}$ ($n$)	$\frac{(-i)^n \pi (2 \pi f)^{n-1} "sgn"(f)}{(n-1)!}$
$\sin(2 \pi f_0 t)$	$\frac{\delta(f – f_0) – \delta(f + f_0)}{2 i}$
$\cos(2 \pi f_0 t)$	$\frac{\delta(f – f_0) + \delta(f + f_0)}{2}$
$u(t) \cdot \sin(2 \pi f_0 t)$	$\frac{f_0}{2 \pi (f_0^2 – f^2)} + \frac{\delta(f – f_0) – \delta(f + f_0)}{4 i}$
$u(t) \cdot \cos(2 \pi f_0 t)$	$\frac{i f}{2 \pi (f_0^2 – f^2)} + \frac{\delta(f – f_0) + \delta(f + f_0)}{4}$
$e^{-\alpha t} u(t)$ (con $\alpha > 0$)	$\frac{1}{a + i 2 \pi f}$
$t \cdot e^{-\alpha t} u(t)$ (con $\alpha > 0$)	$\frac{1}{(a + i 2 \pi f)^2}$
$e^{-\alpha \|t\|}$ (con $\alpha > 0$)	$\frac{2 \alpha}{\alpha^2 + 4 \pi^2 f^2}$
$u(t) e^{- \alpha t} \sin(2 \pi f_0 t)$ (con $\alpha > 0$)	$\frac{2 \pi f_0}{(a + i 2 \pi f)^2 + 4 \pi^2 f_0^2}$
$u(t) e^{- \alpha t} \cos(2 \pi f_0 t)$ (con $\alpha > 0$)	$\frac{a + i 2 \pi f}{(a + i 2 \pi f)^2 + 4 \pi^2 f_0^2}$
$e^{- \frac{t^2}{2 T^2}}$	$T \sqrt{2 \pi} e^{-2 \pi^2 T^2 f^2}$
$"erf"(\alpha t) = \frac{2}{\sqrt{\pi}} \int_0^{\alpha t} e^{-y^2} dy$	$\frac{e^{- (\frac{\pi f}{\alpha})^2}}{i \pi f}$
$e^{2 \pi f_0 t}$ ($f_0 \in \mathbb{C}$)	$\delta(f + i f_0)$
$\sinh(2 \pi f_0 t)$	$\frac{1}{2} [\delta(f + i f_0) – \delta(f – i f_0)]$
$\cosh(2 \pi f_0 t)$	$\frac{1}{2} [\delta(f + i f_0) + \delta(f – i f_0)]$

Somma in $mathbb{R}^n$ e $mathbb{C}^n$, somma fra matrici, prodotto per scalare

Somma in $\mathbb{R}^n$ e in $\mathbb{C}^n$

Gli elementi di $\mathbb{R}^n$ (o più in generale di $\mathbb{C}^n$), possono essere rappresentati come enuple ordinate di numeri reali (rispettivamente complessi) sia come vettori riga, ad esempio

$x = (x_1, x_2, \ldots, x_n)$

che come vettori colonna, ad esempio

$x = ((x_1),(x_2),(\vdots),(x_n))$

La somma fra due vettori riga, o due vettori colonna, è definita come il vettore la cui $i$-esima componente è data dalla somma delle $i$-esime componenti dei due vettori considerati. In formule

$(x_1, x_2, \ldots, x_n) + (y_1, y_2, \ldots, y_n) = (x_1 + y_1, x_2 + y_2, \ldots, x_n + y_n)$

ed equivalentemente

$((x_1),(x_2),(\vdots),(x_n)) + ((y_1),(y_2),(\vdots),(y_n)) = ((x_1 + y_1),(x_2 + y_2),(\vdots),(x_n + y_n))$

Prodotto fra uno scalare e un vettore

Dato uno scalare $\lambda$ (cioè una costante reale o complessa) e un vettore $x \in \mathbb{R}^n$ (o $\in \mathbb{C}^n$), il prodotto $\lambda \cdot x$ è definito come il vettore la cui $i$-esima componente è data dal prodotto fra $\lambda$ e la $i$-esima componente di $x$. In formule

$\lambda \cdot x = \lambda \cdot ((x_1),(x_2),(\vdots),(x_n)) = ((\lambda \cdot x_1),(\lambda \cdot x_2),(\vdots),(\lambda \cdot x_n))$

La situazione è analoga se si considerano vettori riga anziché colonna.

Somma fra matrici

Date due matrici $A$ e $B$ dello stesso ordine $m \times n$ a coefficienti reali (o complessi), la somma $A + B$ è data dalla matrice $C$ di ordine $m \times n$, la cui componente di posto $ij$ equivale alla somma fra la componente di posto $ij$ di $A$ e quella di posto $ij$ di $B$. In formule

se $A = ((a_{11}, \quad a_{12}, \quad \ldots, \quad a_{1n}),(a_{21}, \quad a_{22}, \quad \ldots, \quad a_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(a_{m1}, \quad a_{m2}, \quad \ldots, \quad a_{mn}))$ e $B = ((b_{11}, \quad b_{12}, \quad \ldots, \quad b_{1n}),(b_{21}, \quad b_{22}, \quad \ldots, \quad b_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(b_{m1}, \quad b_{m2}, \quad \ldots, \quad b_{mn}))$

allora

$A + B = ((a_{11}, \quad a_{12}, \quad \ldots, \quad a_{1n}),(a_{21}, \quad a_{22}, \quad \ldots, \quad a_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(a_{m1}, \quad a_{m2}, \quad \ldots, \quad a_{mn})) + ((b_{11}, \quad b_{12}, \quad \ldots, \quad b_{1n}),(b_{21}, \quad b_{22}, \quad \ldots, \quad b_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(b_{m1}, \quad b_{m2}, \quad \ldots, \quad b_{mn})) = ((a_{11} + b_{11}, \quad a_{12} + b_{12}, \quad \ldots, \quad a_{1n} + b_{1n}),(a_{21} + b_{21}, \quad a_{22} + b_{22}, \quad \ldots, \quad a_{2n} + b_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(a_{m1} + b_{m1}, \quad a_{m2} + b_{m2}, \quad \ldots, \quad a_{mn} + b_{mn}))$

Prodotto fra uno scalare e una matrice

Dato uno scalare $\lambda$ (cioè una costante reale o complessa) e una matrice $A$ di ordine $m \times n$, a coefficienti reali o complessi, il prodotto $\lambda \cdot A$ è definito come la matrice di ordine $m \times n$ la cui componente di posto $ij$ è data dal prodotto fra $\lambda$ e la componente di posto $ij$ di $A$. In formule

$\lambda \cdot A = \lambda \cdot ((a_{11}, \quad a_{12}, \quad \ldots, \quad a_{1n}),(a_{21}, \quad a_{22}, \quad \ldots, \quad a_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(a_{m1}, \quad a_{m2}, \quad \ldots, \quad a_{mn})) = ((\lambda \cdot a_{11}, \quad \lambda \cdot a_{12}, \quad \ldots, \quad \lambda \cdot a_{1n}),(\lambda \cdot a_{21}, \quad \lambda \cdot a_{22}, \quad \ldots, \quad \lambda \cdot a_{2n}),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(\lambda \cdot a_{m1}, \quad \lambda \cdot a_{m2}, \quad \ldots, \quad \lambda \cdot a_{mn}))$

Spazi vettoriali

Definizione e proprietà

Dato un campo $K$, un insieme $V$, dotato di due operazioni

$V \times V \to V: (v_1, v_2) \mapsto v_1 + v_2$ (somma fra vettori)

$K \times V \to V: (\lambda, v) \mapsto \lambda \cdot v$ (prodotto per scalare)

si dice spazio vettoriale su $K$ se e solo se sono soddisfatte le seguenti proprietà

1) la somma è commutativa: $v_1 + v_2 = v_2 + v_1 \quad \forall v_1, v_2 \in V$

2) la somma è associativa: $(v_1 + v_2) + v_3 = v_1 + (v_2 + v_3) \quad \forall v_1, v_2, v_3 \in V$

3) esiste in $V$ l’elemento neutro rispetto alla somma, detto vettore nullo e indicato con $O$: $v + O = v \quad \forall v \in V$

4) per ogni elemento $v \in V$, esiste un elemento opposto, $-v \in V$, tale che se sommato a $v$ si ottiene il vettore nullo: $\forall v \in V \quad \exists (-v) \in V: \quad v + (-v) = O$

5) per ogni $v, w \in V$, e per ogni $\lambda, \mu \in K$, il prodotto per scalare rispetta le seguenti proprietà

$(\lambda \mu) v = \lambda (\mu v)$ (il prodotto è associativo)

$(\lambda + \mu) v = \lambda v + \mu v$

$\lambda (v + w) = \lambda v + \lambda w$ (distributività della somma rispetto al prodotto)

$1 \cdot v = 1$ (elemento neutro rispetto al prodotto)

Esempi di spazi vettoriali

1) l’insieme $\mathbb{R}^n$, munito delle usuali operazioni di somma fra vettori e prodotto per scalare, è uno spazio vettoriale su campo $\mathbb{R}$

2) l’insieme $\mathbb{C}^n$, munito delle usuali operazioni di somma fra vettori e prodotto per scalare, è uno spazio vettoriale, e può essere considerato tale sia su $\mathbb{R}$ che su $\mathbb{C}$

3) l’insieme delle matrici di ordine $m \times n$ a coefficienti reali, denotato con $\mathbb{R}^{m \times n}$, munito dell’usuale somma fra matrici e del prodotto righe per colonne è uno spazio vettoriale su $\mathbb{R}$

4) l’insieme delle funzioni reali definite su $[a,b]$, munito delle usuali operazioni di somma e prodotto, definite come

$(f + g)(x) = f(x) + g(x)$

$(\lambda \cdot f)(x) = \lambda \cdot f(x)$

è uno spazio vettoriale su $\mathbb{R}$

Prodotto scalare

Definizione e proprietà

Dato uno spazio vettoriale $V$ su campo $K$, un prodotto scalare è una qualsiasi funzione $f: V \times V \to K$ che rispetta le seguenti proprietà

1) Linearità rispetto alla prima componente:

$f(v_1 + v_2, w) = f(v_1, w) + f(v_2, w) \quad \forall v_1, v_2, w \in V$

2) Omogeneità rispetto alla prima componente:

$f(\lambda v, w) = \lambda \cdot f(v,w) \quad \forall v, w \in V \quad \forall \lambda \in K$

3) Simmetria hermitiana (il soprassegno indica il complesso coniugato):

$f(v,w) = \bar{f(w,v)} \quad \forall v, w \in V$

4) Definita positività di $f(v,v)$ ($O$ è il vettore nullo di $V$):

$f(v,v) \ge 0 \quad \forall v \in V$

$f(v,v) = 0 \iff v = O$

Nel caso particolare di $K = \mathbb{R}$ la proprietà 3) si riduce a $f(v,w) = f(w,v)$ (simmetria), e in tal caso il prodotto scalare risulta simmetrico e bilineare (cioè lineare rispetto ad entrambe le componenti).

Nota: le proprietà 1) – 3) definiscono un funzionale sesquilineare.

Prodotto scalare canonico in $\mathbb{C}^n$

Un particolare prodotto scalare definito in $\mathbb{C}^n$ è il prodotto scalare canonico. Dati due vettori $x = (x_1, x_2, \ldots, x_n)$ e $y = (y_1, y_2, \ldots, y_n)$ di $\mathbb{C}^n$, il prodotto scalare canonico fra $x$ e $y$ si indica con $\langle x, y \rangle$ e vale

$\langle x, y \rangle = \sum_{i=1}^{n} x_i \bar{y_i} = x_1 \bar{y_1} + x_2 \bar{y_2} + \ldots + x_n \bar{y_n}$

Prodotto scalare canonico in $\mathbb{R}^n$

Anche in $\mathbb{R}^n$ si definisce un prodotto scalare canonico, ed è del tutto analogo al precedente. Dati due vettori $x = (x_1, x_2, \ldots, x_n)$ e $y = (y_1, y_2, \ldots, y_n)$ di $\mathbb{R}^n$, il prodotto scalare canonico fra $x$ e $y$ si indica con $\langle x, y \rangle$ e vale

$\langle x, y \rangle = \sum_{i=1}^{n} x_i y_i = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n$

Si può facilmente osservare come in questo secondo caso il prodotto scalare sia commutativo e bilineare.

Norma

Definizione e proprietà

Dato uno spazio vettoriale $V$ su campo $K$, una norma è una qualsiasi funzione $N: V \to \mathbb{R}$ che rispetta queste proprietà

1) Definita positività ($O$ è il vettore nullo di $V$):

$N(v) \ge 0 \quad \forall v \in V$

$N(v) = 0 \iff v = O$

2) Positiva omogeneità:

$N(\lambda v) = |\lambda| N(v) \quad \forall \lambda \in K$

3) Disuguaglianza triangolare (o subadditività):

$N(v_1 + v_2) \le N(v_1) + N(v_2) \quad \forall v_1, v_2 \in V$

Norme indotte da un prodotto scalare

Dato uno spazio vettoriale $V$ su campo $K$, se $f: V \times V \to \mathbb{C}$ è un qualunque prodotto scalare, allora l’applicazione $N: V \to \mathbb{R}$ definita da $N(v) = \sqrt{f(v,v)}$ è una norma. Per questo motivo si dice che ogni prodotto scalare induce una norma, secondo la formula scritta precedentemente.

Caso particolare: norma euclidea

Un tipo particolare di norma definita in $\mathbb{R}^n$ (o più in generale in $\mathbb{C}^n$), è la norma euclidea. Dato un vettore $x = (x_1, x_2, \ldots, x_n)$, la norma euclide di $x$ si indica con $||x||_2$ ed è definita come

$||x||_2 = \sqrt{\sum_{i=1}^n |x_i|^2}$

e nel caso reale si riduce a

$||x||_2 = \sqrt{\sum_{i=1}^n x_i^2}$

La norma euclidea di un vettore di $\mathbb{R}^n$ (o $\mathbb{C}^n$) denota la lunghezza (o modulo) del vettore, e come si può vedere tale norma è indotta dal prodotto scalare.

Nota: mentre ogni prodotto scalare induce una norma, non è detto che ogni norma sia indotta da un prodotto scalare. In altri termini ci sono norme che non possono essere indotte da un prodotto scalare.

Esempi di norme

In $\mathbb{R}^n$, sono delle norme le seguenti applicazioni

1) $||x||_1 = \sum_{i=1}^n |x_i|$ (norma di indice $1$)

2) $||x||_2 = \sqrt{i=1}^n x_i^2$ (norma euclidea, o di indice $2$)

3) $||x||_p = \root{p}{\sum_{i=1}^n |x_i|^p}$, con $p>1$ (norma di indice $p$)

4) $||x||_{\infty} = \max_{i \in \{1, 2, \ldots, n\}} |x_i|$ (norma infinito, ottenuta dalla precedente per $p \to +\infty$)

Nello spazio delle matrici di ordine $m \times n$ a coefficienti reali, sono norme le seguenti applicazioni

1) $||A||_1 = "sup"_{v \in \mathbb{R}^n} ||A v||_1$ (norma matriciale di indice $1$ indotta dalla norma vettorale di indice $1$)

2) $||A||_2 = "sup"_{v \in \mathbb{R}^n} ||A v||_2$ (norma matriciale di indice $2$ indotta dalla norma vettorale di indice $2$)

3) $||A||_p = "sup"_{v \in \mathbb{R}^n} ||A v||_p$, con $p>1$ (norma matriciale di indice $p$ indotta dalla norma vettorale di indice $p$)

4) $||A||_{\infty} = "sup"_{v \in \mathbb{R}^n} ||A v||_{+\infty}$ (norma infinito matriciale indotta dalla norma infinito vettoriale)

Nello spazio delle funzioni continue definite su $[a,b]$ a valori in $\mathbb{R}$, è una norma la seguente applicazione

$||f||_{\infty} = "sup"_{x \in [a,b]} |f(x)|$ (norma infinito)

Nello spazio delle funzione definite su $[a,b]$, derivabili con continuità $k$ volte a valori in $\mathbb{R}$, è una norma la seguente applicazione

$||f||_k = "sup"_{x \in [a,b]} |f^{(k)}(x)| + "sup"_{x \in [a,b]} |f^{(k-1)}(x)| + \ldots + "sup"_{x \in [a,b]} |f'(x)| +"sup"_{x \in [a,b]} |f^(x)|$

Prodotto fra matrici

Date due matrici a coefficienti reali, $A$ di ordine $m \times p$ e $B$ di ordine $q \times n$, il prodotto (righe per colonne) $AB$ è definito solo se il numero di colonne di $A$ è uguale al numero di righe di $B$, cioè se $p = q$. In tal caso il risultato del prodotto è una matrice $C$ di ordine $m \times n$, il cui elemento di posto $ij$ è definito come il prodotto scalare canonico fra la $i$-esima riga di $A$ e la $j$-esima colonna di $B$. In formule

$c_{ij} = \sum_{s=1}^{p} a_{is} b_{sj}$

Esempio: calcolare il prodotto $AB$, dove $A = ((2, \quad 6, \quad 4),(5,\quad 9, \quad 4))$ e $B = ((8,\quad 4),(9,\quad 4),(2, \quad 0))$. $A$ è una matrice di ordine $2 \times 3$, $B$ è di ordine $3 \times 2$, pertanto la matrice risultante $C$ è di ordine $2 \times 2$.

La componente di $C$ di posto $11$ è il prodotto scalare canonico fra la prima riga di $A$ e la prima colonna di $B$, quindi

$c_{11} = \langle (2, 6, 4)", " (8, 9, 2) \rangle = 2 \cdot 8 + 6 \cdot 9 + 4 \cdot 2 = 78$

La componente di $C$ di posto $12$ è il prodotto scalare canonico fra la prima riga di $A$ e la seconda colonna di $B$, quindi

$c_{11} = \langle (2,6, 4)", " (4, 4, 0) \rangle = 2 \cdot 4 + 6 \cdot 4 + 4 \cdot 0 = 32$

La componente di $C$ di posto $21$ è il prodotto scalare canonico fra la seconda riga di $A$ e la prima colonna di $B$, quindi

$c_{11} = \langle (5, 9, 4)", " (8, 9, 2) \rangle = 5 \cdot 8 + 9 \cdot 9 + 4 \cdot 2 = 129$

La componente di $C$ di posto $22$ è il prodotto scalare canonico fra la seconda riga di $A$ e la seconda colonna di $B$, quindi

$c_{11} = \langle (5, 9, 4)", " (4, 4, 0) \rangle = 5 \cdot 4 + 9 \cdot 4 + 4 \cdot 0 = 56$

Quindi la matrice $C$ è

$((78, \quad 32),(129,\quad 56))$

Trasposizione

Se $A$ è una matrice di ordine $m \times n$, allora la matrice $A^T$ ($A$ trasposta) è la matrice di ordine $n \times m$ che si ottiene scambiando le righe con le colonne.

Esempio: se $A = ((1, \quad 2, \quad 3, \quad 4),(5, \quad 6, \quad 7, \quad 8),(9, \quad 10, \quad 11, \quad 12))$ la matrice trasposta è quella che si ottiene scambiando la prima riga con la prima colonna, la seconda riga con la seconda colonna, …, la $n$-esima riga con la $n$-esima colonna, quindi, in questo caso

$A^T = ((1, \quad 5, \quad 9),(2, \quad 6, \quad 10),(3, \quad 7, \quad 11),(4, \quad 8, \quad 12))$

Caso particolare: il trasposto di un vettore riga è il corrispondente vettore colonna, mentre il trasposto di un vettore colonna è il corrispondente vettore riga.

Matrice identità

La matrice identità (indicata con $I$) di ordine $n$ è l’elemento neutro del prodotto fra matrici, ed è una matrice quadrata di ordine $n \times n$ che ha tutti $1$ sulla diagonale principale, e zero altrove.

Proprietà del prodotto fra matrici

$(AB)C = A (BC)$ (proprietà associativa)

$A(B + C) = AB + AC$ (proprietà distributiva)

$(B + C) A = BA + CA$ (proprietà distributiva)

In generale il prodotto non è commutativo, cioè in generale non è vero che $AB = BA$. Tuttavia ci sono dei casi particolari in cui il prodotto risulta commutativo, come il seguente

$A^r A^s = A^s A^r$ $\quad \forall r, z \in \mathbb{Z}$ (le potenze di $A$ commutano)

Infine l’operatore di trasposizione rispetta questa proprietà

$(AB)^T = B^T A^T$

Caso particolare: prodotto fra vettori

Vettore riga per vettore colonna

Se $x = (x_1, x_2, \ldots, x_n)$ e $y = (y_1, y_2, \ldots, y_n)$ sono due vettori a $n$ componenti, il prodotto fra il vettore riga $x$ e il vettore colonna $y$ coincide con il prodotto scalare canonico fra $x$ e $y$, in formule

$(x_1, x_2, \ldots, x_n) ((y_1),(y_2),(\vdots),(y_n)) = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n$

Se $x$ è un vettore riga, il corrispondente vettore colonna si indica con $x^T$ (trasposto), così come se $x$ è un vettore colonna allora il corrispondente vettore riga si indica con $x^T$.

Vettore colonna per vettore riga

Se $x = (x_1, x_2, \ldots, x_n)$ e $y = (y_1, y_2, \ldots, y_n)$ sono due vettori a $n$ componenti, il prodotto fra il vettore colonna $x$ e il vettore riga $y$ coincide con la matrice di ordine $n \times n$ in cui la componente di posto $ij$ è data dal prodotto fra la $i$-esima componente di $x$ e la $j$-esima componente di $y$, in formule

$((x_1),(x_2),(\vdots),(x_n)) (y_1, y_2, \ldots, y_n) = ((x_1 y_1, \quad x_2 y_1, \quad \ldots, \quad x_n y_1),(x_1 y_2, \quad x_2 y_2, \quad \ldots, \quad x_n y_2),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(x_1 y_n, \quad x_2 y_n, \quad \ldots, \quad x_n y_n))$

Determinante di una matrice

Il determinante è definito solo per matrici quadrate, cioè per matrici che hanno lo stesso numero di righe e colonne. Il calcolo del determinante sfrutta un metodo ricorsivo: si definisce il determinante per matrici $1 imes 1$ (cioè costanti) e $2 imes 2$, fatto questo si definisce il determinante di una matrice $n imes n$ come il determinante di una o più matrici $(n-1) imes (n-1)$, e si applica tale regola fino a ricondursi a matrici di ordine $2 imes 2$ o a costanti.

Matrici $1 imes 1$

Il determinante di una matrice $1 imes 1$, cioè di una costante, coincide con la costante stessa, cioè $det(c) = c quad forall c in mathbb{R}$.

Matrici $2 imes 2$

Il determinante di una matrice $2 imes 2$, del tipo

$((a, quad b),(c, quad d))$

vale

$det((a, quad b),(c, quad d)) = ad – bc$

Matrici $n imes n$

Prima di vedere come avviene il calcolo del determinante di una matrice $n imes n$, occorrono due definizioni.

Minore complementare: data una matrice $A$ di ordine $n imes n$, si definisce minore complementare dell’elemento di posto $ij$, e si indica con $M_{ij}$, come il determinante della matrice che si ottiene cancellando l’$i$-esima riga e la $j$-esima colonna.

Complemento algebrico: data una matrice $A$ di ordine $n imes n$, si definisce complemento algebrico dell’elemento di posto $ij$, e si indica con $C_{ij}$, come $C_{ij} = (-1)^{i+j} M_{ij}$, dove $M_{ij}$ è il minore complementare.

Determinante: il determinante di una matrice $A$ quadrata di ordine $n imes n$ equivale alla somma dei prodotti fra gli elementi di una qualunque riga, o colonna, per il rispettivi complementi algebrici. Se ad esempio si scegliesse di sviluppare rispetto alla riga $i$-esima il determinante varrebbe

$det(A) = a_{i1} C_{i1} + a_{i2} C_{i2} + ldots + a_{i n} C_{i n}$

Se invece si scegliesse di sviluppare rispetto alla colonna $j$-esima il determinante varrebbe

$det(A) = a_{1j} C_{1j} + a_{2j} C_{2j} + ldots + a_{nj} C_{nj}$

In entrambi i casi con $a_{ij}$ si intende l’elemento di posto $ij$ della matrice $A$. Il determinante non dipende dalla particolare riga o colonna che si sceglie per lo sviluppo.

Esempio: calcolare il determinante della matrice

$A = ((5, quad 6, quad 3),(1, quad 2, quad 7),(3, quad 4, quad 5))$

Sviluppando rispetto alla prima colonna si ottiene

$det(A) = 5 (-1)^{1+1} det((2, quad 7),(4, quad 5)) + 1 (-1)^{2+1} det((6, quad 3),(4, quad 5)) + 3 (-1)^{3+1} det((6, quad 3),(2, quad 7)) = $

$ = 5 det((2, quad 7),(4, quad 5)) – det((6, quad 3),(4, quad 5)) + 3 det((6, quad 3),(2, quad 7)) = $

$ = 5 (2 cdot 5 – 4 cdot 7) – (6 cdot 5 – 4 cdot 3) + 3 (6 cdot 7 – 2 cdot 3) = -90 -18 + 108 = 0$

Proprietà del determinante

Il determinante della matrice identità è $1$

$det(I) = 1$ (qualunque sia l’ordine di $I$)

Se $A$ è una matrice triangolare superiore (in cui tutti gli elementi sotto la diagonale principale sono nulli), triangolare inferiore (in cui tutti gli elementi sopra la diagonale principale sono nulli), o diagonale (in cui tutti gli elementi sopra e sotto la diagonale principale sono nulli), e $a_1, a_2, ldots, a_n$ sono gli elementi sulla diagonale, allora

$det(A) = a_1 cdot a_2 cdot ldots cdot a_n = prod_{i=1}^n a_i$

Se $A$ e $B$ sono due matrici quadrate dello stesso ordine, allora

$det(A B) = det(A) det(B)$ (teorema di Binet)

Se $det(A)
e 0$, e $B$ è l’inversa di $A$, cioè tale che $AB = I$, allora

$det(A) = frac{1}{det(B)}$

Se $A$ è una matrice quadrata con (almeno) una riga e/o una colonna nulla, allora $det(A) = 0$. Se due righe, o due colonne, sono una multipla dell’altra, allora $det(A) = 0$. In generale se una riga (risp. colonna) è data dalla combinazione lineare delle altre righe (risp. colonne), allora $det(A) = 0$.

Il determinante di una matrice quadrata coincide col determinante della sua trasposta

$det(A) = det(A^T)$

Se $A$ è una matrice quadrata, e $B$ è la matrice ottenuta moltiplicando una riga (o una colonna) di $A$ per $lambda in mathbb{R}$, allora

$det(B) = lambda det(A)$

Se $A$ è una matrice quadrata, e $B$ è una matrice ottenuta ad una riga (o una colonna) di $A$ un’altra riga (o colonna) eventualmente moltiplicata per $lambda in mathbb{R}$, allora

$det(B) = det(A)$

Se $A$ è una matrice quadrata, e $B$ è una matrice ottenuta scambiando di posto due righe, o due colonne, di $A$, allora

$det(B) = – det(A)$

Se $A$ è una matrice quadrata di ordine $n imes n$ allora, per ogni $lambda in mathbb{R}$, vale

$det(lambda cdot A) = lambda^n det(A)$

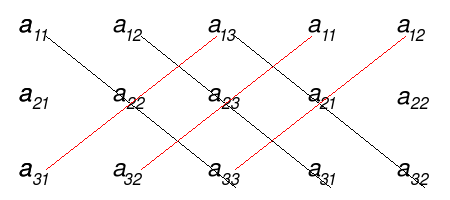
Matrici $3 imes 3$: metodo di Sarrus

Il determinante di matrici di ordine $3 imes 3$ può essere calcolato anche applicando il metodo di Sarrus. A partire da una matrice del tipo

$((a_{11}, quad a_{12}, quad a_{13}),(a_{21}, quad a_{22}, quad a_{23}),(a_{31}, quad a_{32}, quad a_{33}))$

A questo punto si copiano le prime due colonne a fianco della terza, ottenendo una matrice di questo tipo

$((a_{11}, quad a_{12}, quad a_{13}, quad a_{11}, quad a_{12}),(a_{21}, quad a_{22}, quad a_{23}, quad a_{21}, quad a_{22}),(a_{31}, quad a_{32}, quad a_{33}, quad a_{31}, quad a_{32}))$

Ora si eseguono i prodotto secondo le diagonali ilustrate in figura,

si sommano i termini ottenuti seguendo le diagonali nere, e gli si sottraggono quelli ottenuti seguendo le diagonali rosse. Il determinante quindi risulta essere pari a

$a_{11} cdot a_{22} cdot a_{33} + a_{12} cdot a_{23} cdot a_{31} + a_{13} cdot a_{12} cdot a_{32} – a_{31} cdot a_{22} cdot a_{13} – a_{32} cdot a_{23} cdot a_{11} – a_{33} cdot a_{21} cdot a_{12}$

Continuità di funzione definita su intervalli

Determinare, se possibile, le costanti $a, b \in \mathbb{R}$ in modo che la seguente funzione reale di variabile reale sia continua in $\mathbb{R}$.

$f(x) = \{(e^{\frac{1}{x}}, "se " x \in (-\infty, 0)),(a x^4 + b, "se " x \in [0, \frac{\pi}{2}]),(\sin(x), "se " x \in (\frac{\pi}{2}, +\infty)):}$

La funzione è continua in $\mathbb{R} \setminus \{0, \frac{\pi}{2}\}$ indipendentemente dai valori di $a,b$, perché ottenuta per composizione di funzioni continue. Si devono quindi determinare $a, b \in \mathbb{R}$ affinché la funzione sia continua pure in $0$ e $\frac{\pi}{2}$.

La $f$ è continua in $0$ se e solo se

$\lim_{x \to 0^{-}} f(x) = \lim_{x \to 0^{+}} f(x) = f(0)$

$\lim_{x \to 0^{-}} f(x) = \lim_{x \to 0^{-}} e^{\frac{1}{x}} = 0$

$\lim_{x \to 0^{+}} f(x) = \lim_{x \to 0^{+}} a x^4 + b = b$

Affinché i limiti destro e sinistro di zero siano uguali è necessario che valga $b = 0$. Inoltre $f(0) = b$, pertanto, scegliendo $b=0$, la funzione risulta continua in $0$. Ragionando allo stesso modo per $\frac{\pi}{2}$, e considerando $b=0$, si ottiene

$\lim_{x \to \frac{\pi}{2}^{-}} f(x) = \lim_{x \to \frac{\pi}{2}^{-}} a x^4 = a \frac{\pi^4}{16}$

$\lim_{x \to \frac{\pi}{2}^{+}} f(x) = \lim_{x \to \frac{\pi}{2}^{+}} \sin(x) = 1$

Affinché i limiti destro e sinistro siano uguali è necessario scegliere $a=\frac{16}{\pi^4}$. Dato che $f(\frac{\pi}{2}) = a \frac{\pi^4}{16}$, con la scelta $a=\frac{16}{\pi^4}$ la funzione risulta continua pure in $\frac{\pi}{2}$.

In conclusione, affinché la $f$ sia continua in tutto $\mathbb{R}$, è necessario scegliere $a = \frac{16}{\pi^4}$ e $b = 0$.

FINE

Proprietà topologiche in $mathbb{R}^2$

Sia $D \subset \mathbb{R}^2$ il dominio di definizione della funzione

$f(x,y) = \sqrt{x^2 – 4} \cdot \log(36 – 4x^2 – 9y^2)$

Disegnarlo, determinare la frontiera e stabilire se $D$ è aperto, chiuso, limitato, compatto, e da quante componenti connesse è composto.

Una radice quadrata è definita quando il radicando è non negativo, un logaritmo invece ha senso se l'argomento è positivo, pertanto il dominio della funzione si può trovare risolvendo il seguente sistema

$\{(x^2 – 4 \ge 0),(36 – 4x^2 – 9y^2 > 0):} = \{(x \le -2 \quad \vee \quad x \ge 2),(\frac{x^2}{9} + \frac{y^2}{4} < 1):}$

Quindi $D = \{(x,y) \in \mathbb{R}^2: x^2 – 4 \ge 0, \frac{x^2}{9} + \frac{y^2}{4} < 1\}$

La frontiera dell'insieme è

$\partial D = \{(-2,y) \in \mathbb{R}^2: – \sqrt{\frac{28}{9}} \le y \le \sqrt{\frac{28}{9}}\} \cup \{(2,y) \in \mathbb{R}^2: – \sqrt{\frac{28}{9}} \le y \le \sqrt{\frac{28}{9}}\} \cup \{(x,y) \in \mathbb{R}^2: \frac{x^2}{9} + \frac{y^2}{4} = 1, x \le -2\} \cup \{(x,y) \in \mathbb{R}^2: \frac{x^2}{9} + \frac{y^2}{4} = 1, x \ge 2\}$

Dato che $\partial D \cap D \ne \emptyset$, e che la frontiera di $D$ non è interamente contenuta in $D$, l'insieme non è aperto né chiuso.

Il dominio $D$ è un insieme limitato, esiste infatti un intorno sferico aperto dell'origine (ad esempio di raggio $10$) che lo contenga propriamente.

Infine $D$ non è connesso per archi, ma possiede due componenti connesse.

FINE

Inversa di una matrice

Se $A$ è una matrice quadrata di ordine $n \times n$, ed esiste una matrice $B$ tale che $AB = I$, si dice che $B$ è l’inversa di $A$, e si scrive $B = A^{-1}$.
Una matrice quadrata $A$ ammette un’inversa se e solo se $\det(A) \ne 0$, e in tal caso si dice invertibile (una matrice con determinante nullo si dice singolare). Quando una matrice ammette un’inversa, essa è unica.

Calcolo dell’inversa

Se $A$ è una matrice quadrata, e $\det(A) \ne 0$, la matrice inversa è data da

$A^{-1} = \frac{1}{det(A)} M^T$

$M$ viene detta matrice dei complementi algebrici, dato che l’elemento di posto $ij$ di $M$ coincide con il complemento algebrico dell’elemento di posto $ij$ di $A$, mentre l’apice $T$ sta ad indicare l’operatore di trasposizione.

Esempio: calcolare l’inversa della matrice

$A = ((2, \quad 3, \quad 5),(1, \quad 6, \quad 1),(0, \quad 2, \quad 3))$

Il determinante di $A$ vale

$\det(A) = 2 \cdot \det((6, \quad 1),(2, \quad 3)) – \det((3, \quad 5),(2, \quad 3)) = 32 + 1 = 33$

I complementi algebrici degli elementi di $A$ valgono

$c_{11} = (-1)^{1 + 1} \cdot det((6, \quad 1),(2, \quad 3)) = 16$

$c_{12} = (-1)^{1 + 2} \cdot det((1, \quad 1),(0, \quad 3)) = -3$

$c_{13} = (-1)^{1 + 3} \cdot det((1, \quad 6),(0, \quad 2)) = 2$

$c_{21} = (-1)^{2 + 1} \cdot det((3, \quad 5),(2, \quad 3)) = 1$

$c_{22} = (-1)^{2 + 2} \cdot det((2, \quad 5),(0, \quad 3)) = 6$

$c_{23} = (-1)^{2 + 3} \cdot det((2, \quad 3),(0, \quad 2)) = -4$

$c_{31} = (-1)^{3 + 1} \cdot det((3, \quad 5),(6, \quad 1)) = -27$

$c_{32} = (-1)^{3 + 2} \cdot det((2, \quad 5),(1, \quad 1)) = 3$

$c_{33} = (-1)^{3 + 3} \cdot det((2, \quad 3),(1, \quad 6)) = 9$

Quindi la matrice inversa è

$A^{-1} = \frac{1}{33} ((16, \quad -3, \quad 2),(1, \quad 6, \quad -4),(-27, \quad 3, \quad 9))^T = \frac{1}{33} ((16, \quad 1, \quad -27),(-3, \quad 6, \quad 3),(2, \quad -4, \quad 9))$

Caso particolare: matrice $2 \times 2$

Se $A$ è una matrice quadrata di ordine $2 \times 2$ invertibile, cioè

$A = ((a, \quad b),(c, \quad d))$ con $\det(A) = ad – bc \ne 0$

la matrice inversa è

$A^{-1} = \frac{1}{\det(A)} ((d, \quad -b),(-c, \quad a))$

Come si vede in questo caso la matrice dei complementi algebrici trasposta si ottiene da $A$ scambiando gli elementi sulla diagonale principale e invertendo il segno degli altri due.

Studiare al convergenza semplice e assoluta $sum_{n=1}^{+infty} (-1)^n log(1 + frac{1}{n})$

Studiare al convergenza semplice e assoluta della seguente serie a termini di segno alterno

$\sum_{n=1}^{+\infty} (-1)^n \log(1 + \frac{1}{n})$

Dato che $1 + \frac{1}{n} > 1$ $\forall n \in \mathbb{N} \setminus \{0\}$ allora $\log(1 + \frac{1}{n}) > 0$ $\forall n \in \mathbb{N} \setminus \{0\}$, pertanto la serie è effettivamente a termini di segno alterno.

Visto che

$1 + \frac{1}{n + 1} < 1 + \frac{1}{n}$ $\forall n \in \mathbb{N} \setminus \{0\}$

allora la successione $\{1 + \frac{1}{n}\}_{n \ge 1}$ è monotona decrescente, pertanto anche la successione $\{\log(1 + \frac{1}{n})\}_{n \ge 1}$ è monotona decrescente, visto che il logaritmo in base $e$ è una funzione monotona crescente. Pertanto la serie proposta converge semplicemente per il criterio di Leibniz.

Per studiare la convergenza assoluta occorre considerare la serie

$\sum_{n=1}^{+\infty} |(-1)^n \log(1 + \frac{1}{n})| = \sum_{n=1}^{+\infty} |\log(1 + \frac{1}{n})| = \sum_{n=1}^{+\infty} \log(1 + \frac{1}{n})$

per quanto detto prima sulla positività di $\log(1 + \frac{1}{n})$ quando $n=1,2,\ldots$.

Osservando che

$\lim_{n \to +\infty} \frac{\log(1 + \frac{1}{n})}{\frac{1}{n}} = 1$

si nota che

$\log(1 + \frac{1}{n}) \sim \frac{1}{n}$

$\sum_{n=1}^{+\infty} \frac{1}{n}$

diverge, perché è una serie armonica con esponente pari a $1$, pertanto la serie proposta non converge assolutamente per il criterio del confronto asintotico.

FINE

Studiare il carattere della seguente serie a termini positivi$sum_{n=1}^{+infty} {3^n}/((n-1)!)$.

Studiare il carattere della seguente serie a termini positivi

$\sum_{n=1}^{+\infty} \frac{3^n}{(n-1)!}$

Dato che

$\lim_{n \to +\infty} \frac{\frac{3^{n+1}}{n!}}{\frac{3^n}{(n-1)!}} = \lim_{n \to +\infty} \frac{3^{n+1}}{n!} \cdot \frac{(n-1)!}{3^n} = \lim_{n \to +\infty} \frac{3}{n} = 0 < 1$

la serie proposta converge per il criterio del rapporto.

FINE

Max, min, sup, inf per sottoinsiemi di $mathbb{R}$

Stabilire se il seguente insieme è limitato superiormente, inferiormente. Determinare (se esistono) l'estremo superiore, l'estremo inferiore, il massimo e il minimo assoluto.

$\{x \in \mathbb{R}: \sqrt{x^2 + x – 6} >1\}$

Affinché la radice abbia senso, è necessario che il radicando sia non negativo:

$x^2 + x – 6 \ge 0$ (1)

Le soluzioni dell'equazione associata sono

$x_{1,2} = \frac{-1 \pm \sqrt{1 + 24}}{2} = \frac{-1 \pm 5}{2}$

$x_1 = -3 \quad x_2 = 2$

pertanto la (1) è soddisfatta per

$x \le -3 \quad \vee \quad x \ge 2$ (3)

La diseuquazione

$\sqrt{x^2 + x – 6} \ge 1$

è soddisfatta se vale (3) e se

$x^2 + x – 6 \ge 1$ (4)

Le soluzioni dell'equazione associata sono

$x_{1,2} = \frac{-1 \pm \sqrt{1+28}}{2} = \frac{-1 \pm \sqrt{29}}{2}$

pertanto la (4) è soddisfatta per

$x < \frac{-1 – \sqrt{29}}{2} \quad \vee \quad x > \frac{-1 + \sqrt{29}}{2}$

quindi, tenendo conto anche di (3), l'insiemee iniziale si può riscrivere come

$\{x \in \mathbb{R}: x < \frac{-1 – \sqrt{29}}{2} \quad \vee \quad x > \frac{-1 + \sqrt{29}}{2}\} = ]-\infty, \frac{-1 – \sqrt{29}}{2}[ \quad \cup \quad ]\frac{-1 + \sqrt{29}}{2}, +\infty[$

Pertanto l'insieme è illimitato sia superiormente che inferiormente. Non ammettené minimo assoluto né massimo assoluto, l'estremo inferiore e superiore coincidono rispettivamente con $-\infty$ e $+\infty$.

FINE

Autovalori di una matrice

Data una matrice $A \in \mathbb{R}^{n \times n}$, gli autovalori, reali o complessi, di $A$ sono tutte e sole le costanti $\lambda \in \mathbb{C}$ tali per cui la matrice $\lambda I – A$ risulta singolare ($I$ è la matrice identità dello stesso ordine di $A$).

Calcolo degli autovalori

1) A partire dalla matrice $A$, il primo passo è quello di costruire la matrice $\lambda I – A$, e di calcolarne il determinante. Tale determinante si chiama polinomio caratteristico, e si indica con $p(\lambda)$.

2) Come secondo passo si risolve l’equazione $p(\lambda) = 0$; le soluzioni di tale equazione sono gli autovalori di $A$.

3) Se $\lambda_i$ è una radice del polinomio caratteristico, quindi un autovalore, si dice molteplicità algebrica di $\lambda_i$ la molteplicità di $\lambda_i$ come radice del polinomio caratteristico.

Dato che $A \in \mathbb{R}^{n \times n}$, il polinomio caratteristico è un polinomio a coefficienti reali di grado $n$. Questo vuol dire che ammette esattamente $n$ radici in $\mathbb{C}$, ognuna contata con la sua molteplicità, e inoltre se $\lambda_i$ è una radice complessa di $p(\lambda)$, allora anche $\bar{\lambda_i}$ è radice di $p(\lambda)$.

Quindi una matrice quadrata a coefficienti reali di ordine $n$ ha esattamente $n$ autovalori (reali o complessi) ognuno contato con la sua molteplicità, e inoltre se $\lambda_i$ è un autovalore complesso, allora anche il suo complesso coniugato è un autovalore.

Esempio: calcolare gli autovalori (reali o complessi) della matrice

$A = ((0, \quad 1, \quad 0),(-2, \quad -3, \quad \frac{1}{2}),(0, \quad 0, \quad 0))$

Per prima cosa si costruisce la matrice $\lambda I – A$

$\lambda I – A = \lambda ((1, \quad 0, \quad 0),(0, \quad 1, \quad 0),(0, \quad 0, \quad 1)) – ((0, \quad 1, \quad 0),(-2, \quad -3, \quad \frac{1}{2}),(0, 0, 0)) = ((\lambda, \quad 0, \quad 0),(0, \quad \lambda, \quad 0),(0, \quad 0, \quad \lambda)) – ((0, \quad 1, \quad 0),(-2, \quad -3, \quad \frac{1}{2}),(0, 0, 0)) = ((\lambda, \quad -1, \quad 0),(2, \quad \lambda + 3, \quad -\frac{1}{2}),(0, \quad 0, \quad \lambda))$

Adesso occorre calcolare il determinante di questa matrice: sviluppando rispetto all’ultima riga si ottiene

$p(\lambda) = \lambda \cdot \det((\lambda, \quad -1),(2, \quad \lambda + 3)) = \lambda (\lambda^2 + 3 \lambda + 2)$

Ponendo $p(\lambda = 0)$ si ottiene $\lambda (\lambda^2 + 3 \lambda + 2) = 0$, da cui

$\lambda_1 = 0$

$\lambda^2 + 3 \lambda + 2 = 0 \implies \lambda_2 = -2, \quad \lambda_3 = -1$

Quindi gli autovalori di $A$ sono $-2, -1, 0$, ed hanno tutti molteplicità algebrica pari a uno.

Autovettori e autospazi

Definizione

Data una matrice $A \in \mathbb{R}^{n \times n}$, sia $\lambda_i \in \mathbb{C}$ un suo autovalore. Si dice che $v \in \mathbb{C}^n \setminus \{0\}$ ($v$ vettore di $\mathbb{C}^n$ diverso dal vettore nullo) è un autovettore di $A$ relativo all’autovalore $\lambda_i$ se e solo se risulta

$A v = \lambda_i v$

o equivalentemente

$(\lambda_i I – A) v = O$

Lo spazio vettoriale generato dagli autovettori relativi a $\lambda_i$ si chiama autospazio di $A$ relativo all’autovalore $\lambda_i$. La dimensione di tale autospazio si chiama molteplicità geometrica dell’autovalore $\lambda_i$.

Per ogni autovalore $\lambda_i$, se $\mu_i$ indica la sua molteplicità algebrica e $\nu_i$ indica la sua molteplicità geometrica, vale

$0 < \nu_i \le \mu_i$

Quindi se un autovalore ha molteplicità algebrica $1$, allora ha necessariamente molteplicità geometrica pari a $1$.

Calcolo degli autovettori

1) Data $A \in \mathbb{R}^{n \times n}$. si calcolano gli autovalori della matrice $A$

2) Considerato l’autovalore $\lambda_i$, si costruisce il sistema $(\lambda_i I – A) v = O$

3) Tutte le soluzioni non banali, cioè tutti i vettori $v$ diversi dal vettore nullo, che risolvono il sistema sono gli autovettori di $A$ relativi all’autovalore $\lambda_i$

4) Si ripetono i punti 2) e 3) per tutti gli autovalori trovati al punto 1)

Esempio: calcolo degli autovettori della matrice

$A = ((0, \quad 1, \quad 0),(-2, \quad -3, \quad \frac{1}{2}),(0, \quad 0, \quad 0))$

Gli autovalori di $A$ sono $\lambda_1 = 0$, $\lambda_2 = -2$, $\lambda_3 = -1$. Per calcolare gli autovettori relativi a $\lambda_1$ si calcola la matrice $\lambda_1 I – A$ e si imposta il sistema $(\lambda_1 I – A) v = O$

$\lambda_1 I – A = – A = ((0, \quad -1, \quad 0),(2, \quad 3, \quad -\frac{1}{2}),(0, \quad 0, \quad 0))$

da cui

$(\lambda_1 I – A) v = O \implies ((0, \quad -1, \quad 0),(2, \quad 3, \quad -\frac{1}{2}),(0, \quad 0, \quad 0)) ((v_1),(v_2),(v_3)) = ((0),(0),(0)) \implies \{(- v_2 = 0),(2 v_1 + 3 v_2 – \frac{1}{2} v_3 = 0),(0 = 0):}$

Ponendo $v_3 = \alpha$ come parametro libero, dove $\alpha \in \mathbb{R} \setminus \{0\}$, si ottiene

$\{(-v_2 = 0),(v_1 = \frac{1}{4} v_3),(v_3 = \alpha):} = \{(v_1 = \frac{\alpha}{4}),(v_2 = 0),(v_3 = \alpha):}$

Al variare di $\alpha \in \mathbb{R} \setminus \{0\}$ il generico autovettore relativo a $\lambda_1$ è

$v = ((\frac{\alpha}{4}),(0),(\alpha)) = \alpha ((\frac{1}{4}),(0),(1))$

Una base per l’autospazio relativo all’autovalore $\lambda_1$ è $\{(\frac{1}{4}, 0, 1)}$. Dato che la dimensione dell’autospazio è $1$ la molteplicità gemetrica di tale autovalore è $1$ (come era logico aspettarsi, dato che è $1$ la molteplicità algebrica).

Per calcolare gli autovettori relativi a $\lambda_2$ si calcola la matrice $\lambda_2 I – A$ e si imposta il sistema $(\lambda_2 I – A) v = O$

$\lambda_2 I – A = – 2 I – A = ((-2, \quad -1, \quad 0),(2, \quad 1, \quad -\frac{1}{2}),(0, \quad 0, \quad -2))$

da cui

$(\lambda_2 I – A) v = O \implies ((-2, \quad -1, \quad 0),(2, \quad 1, \quad -\frac{1}{2}),(0, \quad 0, \quad -2)) ((v_1),(v_2),(v_3)) = ((0),(0),(0)) \implies$

$\implies \{(-2 v_1 – v_2 = 0),(2 v_1 + v_2 – \frac{1}{2} v_3 = 0),(-2 v_3 = 0):} \implies \{(v_2 = -2 v_1),(-2 v_1 + 2 v_1 = 0),(v_3 = 0):}$

Ponendo $v_2 = \alpha$ come parametro libero, dove $\alpha \in \mathbb{R} \setminus \{0\}$, si ottiene

$\{(v_1 = -\frac{v_2}{2}),(v_2 = \alpha),(v_3 = 0):}$

Al variare di $\alpha \in \mathbb{R} \setminus \{0\}$ il generico autovettore relativo a $\lambda_2$ è

$v = ((-\frac{\alpha}{2}),(\alpha),(0)) = \alpha ((-\frac{1}{2}),(1),(0))$

Una base per l’autospazio relativo all’autovalore $\lambda_2$ è $\{(-\frac{1}{2}, 1, 0)}$. Dato che la dimensione dell’autospazio è $1$ la molteplicità gemetrica di tale autovalore è $1$ (come era logico aspettarsi, dato che è $1$ la molteplicità algebrica).

Per calcolare gli autovettori relativi a $\lambda_3$ si calcola la matrice $\lambda_3 I – A$ e si imposta il sistema $(\lambda_3 I – A) v = O$

$\lambda_3 I – A = – I – A = ((-1, \quad -1, \quad 0),(2, \quad 2, \quad -\frac{1}{2}),(0, \quad 0, \quad -1))$

da cui

$(\lambda_3 I – A) v = O \implies ((-1, \quad -1, \quad 0),(2, \quad 2, \quad -\frac{1}{2}),(0, \quad 0, \quad -1)) ((v_1),(v_2),(v_3)) = ((0),(0),(0)) \implies$

$\implies \{(-v_1 – v_2 = 0),(2 v_1 + 2 v_2 – \frac{1}{2} v_3 = 0),(-v_3 = 0):} \implies \{(v_1 = – v_2),(0 = 0),(v_3 = 0):}$

Ponendo $v_2 = \alpha$ come parametro libero, dove $\alpha \in \mathbb{R} \setminus \{0\}$, si ottiene

$\{(v_1 = -\alpha),(v_2 = \alpha),(v_3 = 0):}$

Al variare di $\alpha \in \mathbb{R} \setminus \{0\}$ il generico autovettore relativo a $\lambda_3$ è

$v = ((-\alpha),(\alpha),(0)) = \alpha ((-1),(1),(0))$

Una base per l’autospazio relativo all’autovalore $\lambda_3$ è $\{(-1, 1, 0)}$. Dato che la dimensione dell’autospazio è $1$ la molteplicità gemetrica di tale autovalore è $1$ (come era logico aspettarsi, dato che è $1$ la molteplicità algebrica).

Diagonalizzazione

Definizione

Una matrice $A \in \mathbb{R}^{n \times n}$ si dice diagonalizzabile (su $\mathbb{C}$) se e solo se esiste una matrice $T \in \mathbb{C}^{n \times n}$ invertibile tale che

$\Lambda = T^{-1} A T$

dove $\Lambda$ è una matrice in forma diagonale.

Calcolo di $\Lambda$ e $T$

1) se la matrice $A$ è diagonalizzabile, allora gli elementi sulla diagonale di $\Lambda$ sono gli autovalori di $A$, ripetuti con la loro molteplicità algebrica

2) per stabilire se una matrice $A$ è diagonalizzabile

– si calcolano gli autovalori $\lambda_1 , \lambda_2 , \ldots, \lambda_m \in \mathbb{C}$ di $A$

– per ciascun autovalore si calcola la molteplicità algebrica $\mu_i$

– per ciascun autovalore si calcola la molteplicità geometrica $\nu_i$

– se $\mu_i = \nu_i$ per ogni autovalore allora la matrice $A$ è diagonalizzabile

3) per determinare la matrice di cambio di coordinate $T$ si devono distinguere due casi

1° caso: tutti gli autovalori di $A$ sono reali

2° caso: esiste almeno un autovalore di $A$ complesso

1° caso: autovalori tutti reali

Supponiamo che $A \in \mathbb{R}^{n \times n}$ sia diagonalizzabile, e siano $\lambda_1 , \lambda_2 , \ldots , \lambda_m \in \mathbb{R}$ i suoi autovalori, con molteplicità algebrica pari a, rispettivamente, $\mu_1, \mu_2, \ldots, \mu_m$.

Sia $V_i$ l’autospazio relativo all’autovalore $\lambda_i$, allora $\dim(V_i) = \nu_i = \mu_i$, dato che $A$ è diagonalizzabile, e una base di $V_i$ è data da $\mu_i$ autovettori linearmente indipendenti relativi a $\lambda_i$, cioè

$\{ v_{i1}, v_{i2}, \ldots, v_{i \mu_i}\}$ (i vettori sono intesi come colonne)

Ripetendo lo stesso ragionamento per tutti gli autovalori si trovano le basi di tutti gli autospazi (ognuno relativo ad un autovalore). Quindi se

$\{v_{11}, v_{12}, \ldots, v_{1 \mu_1}\} = "base dell’autospazio relativo a " \lambda_1$

$\{v_{21}, v_{22}, \ldots, v_{2 \mu_2}\} = "base dell’autospazio relativo a " \lambda_2$

$\vdots$

$\{v_{m1}, v_{m2}, \ldots, v_{m \mu_m}\} = "base dell’autospazio relativo a " \lambda_m$

allora la matrice del cambio di coordinate è data da

$T = [ v_{11} \quad v_{12} \quad \ldots \quad v_{1 \mu_1} \quad | \quad v_{21} \quad v_{22} \quad \ldots \quad v_{2 \mu_2} \quad | \quad \ldots \quad | \quad v_{m 1} \quad v_{m 2} \quad \ldots \quad v_{m \mu_m} ]$

La matrice $\Lambda$, data da $\Lambda = T^{-1} A T$, è invece pari a

$T = "diag"(\lambda_1 , \lambda_1 , \ldots, \lambda_1 , \lambda_2 , \lambda_2 , \ldots , \lambda_2 , \ldots , \lambda_m , \lambda_m , \ldots, \lambda_m)$

ossia è la matrice diagonale che ha sulla diagonale principale gli autovalori di $A$, ognuno ripetuto un numero pari di volte alla sua molteplicità algebrica.

2° caso: matrice con autovalori complessi

Sia $A \in \mathbb{R}^{n \times n}$ la matrice diagonalizzabile considerata, e sia $\lambda \in \mathbb{C}$, un suo autovalore complesso, quindi della forma $\lambda = \sigma + i \omega$, con $\omega > 0$. Dato che $A$ è a coefficienti reali, allora anche $\bar{\lambda} = \sigma – i \omega$ è un autovalore.

Se $\lambda$ è un autovalore complesso, allora gli autovettori ad esso relativo sono complessi, e si possono scrivere come

$v = v^{(1)} + i v^{(2)}$, con $v^{(1)}, v^{(2)} \in \mathbb{R}^n$

Si dimostra che $v^{(2)}$ è diverso dal vettore nullo, e che $v^{(1)}$ e $v^{(2)}$ sono linearmente indipendenti. Se $v$ è un autovettore relativo a $\lambda = \sigma + i \omega$, allora

$\bar{v} = v^{(1)} – i v^{(2)}$

è un autovettore relativo a $\bar{\lambda} = \sigma – i \omega$.

Indichiamo con $\lambda_{1}, \lambda_{2}, \ldots, \lambda_{r} \in \mathbb{R}$ gli autovalori reali di $A$, e indichiamo con $\lambda_{r+1}, \lambda_{r+2}, \ldots, \lambda_{c} \in \mathbb{C}$ gli autovalori complessi di $A$ con parte reale positiva.

Nota: $\lambda_{r+1}, \lambda_{r+2}, \ldots, \lambda_{c}$ non sono tutti gli autovalori complessi di $A$, dato che anche i rispettivi complessi coniugati lo sono

Nota: gli autovalori complessi $\lambda_i$ si possono scrivere come $\lambda_i = \sigma_i + i \omega_i$, con $\omega_i > 0$ e $r+1 \le i \le c$

Ipotesi semplificativa: supponiamo che ogni autovalore complesso abbia molteplicità algebrica e geometrica pari a $1$. In tal caso la base dell’autospazio relativo ad un autovalore complesso $\lambda_i$ sarà data da un vettore $v_i \ne 0$, e inoltre

$v_i = v_i^{(1)} + i v_i^{(2)}$, con $v_i^{(1)}, v_i^{(2)} \in \mathbb{R}^n$

Ripetendo questo ragionamento per tutti gli autovalori complessi, e calcolando le basi per gli autospazi relativi ad autovalori reali, come nel caso precedente, si trova questa matrice di cambio di coordinate

$T = [v_1 \quad v_2 \quad \ldots \quad v_r \quad | \quad v_{r+1}^{(1)} \quad v_{r+1}^{(2)} \quad | \quad \ldots \quad | \quad v_{c}^{(1)} \quad v_c^{(2)}]$

In questo modo il prodotto $T^{-1} A T$ coincide con la matrice

$[(\lambda_1, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(0, \quad \lambda_2, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(\vdots, \quad 0, \quad \ddots, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad 0, \quad \lambda_{r}, \quad 0, \quad 0, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad 0, \quad \sigma_{r+1}, \quad \omega_{r+1}, \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad 0, \quad -\omega_{r+1}, \quad \sigma_{r+1}, \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad 0, \quad \ddots, \quad \ddots, \quad 0, \quad 0),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad 0, \quad \sigma_c, \quad \omega_c),(0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0, \quad -\omega_c, \quad \sigma_c)]$

Questa è la forma diagonale reale a blocchi della matrice $A$. I primi $r$ elementi sulla diagonale principale sono gli autovalori reali di $A$, nelle altre parti della diagonale principale ci sono invece dei blocchi $2 \times 2$, ognuno relativo ad un autovalore complesso (con parte immaginaria positiva). Infatti, all’autovalore $\lambda_i = \sigma_i + i \omega_i$, $\omega_i > 0$, corrisponde il blocco

$[(\sigma_{i}, \omega_{i}),(-\omega_{i}, \sigma_i)]$

Nota: la forma diagonale della matrice $A$ è data da

$\Lambda = "diag"(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{r}, \lambda_{r+1}, \bar{\lambda_{r+2}} \ldots, \lambda_{c}, \bar{\lambda_c})$

Potenza di una matrice

Definizione

Data una matrice $A \in \mathbb{R}^{n \times n}$, la potenza $k$-esima di $A$ ($k \in \mathbb{N}$), è definita ricorsivamente così come segue

$A^k = \{(I, \quad "se " k = 0),(A^{k-1} \cdot A, \quad "se " k > 0):}$

Potenza di una matrice diagonalizzabile

Se $A \in \mathbb{R}^{n \times n}$ è una matrice diagonalizzabile, il calcolo della potenza $k$-esima $A^k$ può essere effettuato senza bisogno di ricorrere alla definizione. Detta $T$ la matrice del cambio di coordinate, risulta

$A = T \Lambda T^{-1}$

dove $\Lambda$ è una matrice in forma diagonale se tutti gli autovalori di $A$ sono reali, mentre è in forma daigonale reali a blocchi se $A$ ammette autovalori complessi. In entrambi i casi la potenza $k$-esima di $A$ vale

$A^k = T \Lambda^k T^{-1}$

Nel caso di matrici diagonalizzabili dunque è sufficiente calcolare, oltre alla matrice del calcolo di coordinate, la potenza della matrice diagonalizzata, e tale calcolo è relativamente semplice.

Nel calcolo di $\Lambda^k$ si distinguono i casi in cui $\Lambda$ è una matrice in forma diagonale da quello in cui $\Lambda$ è in forma diagonale reale a blocchi.

$A$ ha tutti gli autovalori reali

Se la matrice $A$ ha tutti gli autovalori reali, e questi sono pari a $\lambda_{1}, \lambda_{2}, \ldots, \lambda_n$, ed inoltre se $T$ è la matrice del cambio di coordinate, allora

$A = T \Lambda T^{-1}$

dove

$\Lambda = ((\lambda_{1}, \quad 0, \ldots, 0),(0, \lambda_{2}, \quad \ldots, 0),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(0, \quad 0, \quad \ldots, \quad \lambda_n))$

La potenza $k$-esima di $\Lambda$ è banalmente la matrice ottenuta calcolando la potenza $k$-esima degli elementi sulla diagonale principale

$\Lambda^k = ((\lambda_{1}^k, \quad 0, \ldots, 0),(0, \lambda_{2}^k, \quad \ldots, 0),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(0, \quad 0, \quad \ldots, \quad \lambda_n^k))$

Pertanto, in questo caso, la potenza $k$-esima di $A$ vale

$A^k = T \Lambda^k T^{-1}$

$A$ ha almeno un autovalore complesso

Supponiamo ora che $A$ abbia autovalori complessi, e che i suoi autovalori siano $\lambda_{1}, \lambda_{2}, \ldots, \lambda_{r}, \lambda_{r+1}, \bar{\lambda_{r+1}}, \lambda_{r+2}, \bar{\lambda_{r+2}}, \ldots, \lambda_{c}, \bar{\lambda_{c}}$, dove i primi $r$ sono reali, i restanti sono complessi. Scriviamo ogni autovalore complesso con parte immaginaria positiva come

$\lambda_i = \sigma_i + i \omega_i$

Se $T$ è la matrice del cambio di coordinate, allora $A = T \Lambda T^{-1}$, dove $\Lambda$ è una matrice in forma diagonale reale a blocchi, della forma

$\Lambda = [(\lambda_1, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(0, \quad \lambda_2, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(\vdots, \quad 0, \quad \ddots, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad 0, \quad \lambda_{r}, 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad 0, \quad \sigma_{r+1}, \quad \omega_{r+1}, \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad -\omega_{r+1}, \quad \sigma_{r+1}, \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad 0, \quad \ddots, \quad 0, \quad 0),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad \vdots, \quad \sigma_c, \quad \omega_c),(0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0, \quad -\omega_c, \quad \sigma_c)]$

Per ogni autovalore complesso $\lambda_i = \sigma_i + i \omega_i$ (a cui corrisponde un blocco $2 \times 2$ sulla diagonale di $\Lambda$), indichiamo con $\rho_i$ il suo modulo e con $\theta_i$ la sua fase, ossia

$\rho_i = \sqrt{\sigma_i^2 + \omega_i^2} \qquad \theta_i = "arctg"(\frac{\omega_i}{\sigma_i})$

Fatto questo si può scrivere la potenza $k$-esima di $\Lambda$, che è pari a

$\Lambda^k = [(\lambda_1^k, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(0, \quad \lambda_2^k, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(\vdots, \quad 0, \quad \ddots, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad 0, \quad \lambda_{r}^k, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad 0, \quad \rho_{r+1}^k \cos(k \theta_{r+1}),\quad \rho_{r+1}^k \sin(k \theta_{r+1}), \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad -\rho_{r+1}^k \sin(k \theta_{r+1}), \quad \rho_{r+1}^k \cos(k \theta_{r+1}), \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad 0, \quad \ddots, \quad 0, \quad 0),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad \vdots, \quad \rho_{c}^k \cos(k \theta_{c}), \quad \rho_{c}^k \sin(k \theta_{c})),(0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0, \quad -\rho_{c}^k \sin(k \theta_{c}), \quad \rho_{c}^k \cos(k \theta_{c}))]$

Una volta calcolata $\Lambda^k$ è possibile calcolare anche la potenza $k$-esima di $A$, dato che

$A^k = T \Lambda^k T^{-1}$

$frac{x^2}{a^2} + frac{y^2}{b^2} = 1$

Calcolare l’area dell’ellisse avente equazione cartesiana

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

L’area richiesta equivale a

$\int \int_{A} dxdy$

dove

$A = \{(x,y) \in \mathbb{R}^2: \frac{x^2}{a^2} + \frac{y^2}{b^2} \le 1\}$

Conviene passare in coordinate polari, ponendo

$\{(x = a \rho \cos(\theta)),(y = b \rho \sin(\theta)):}$

con $\rho \in [0, +\infty)$ e $\theta \in [0, 2 \pi]$. La matrice Jacobiana associata alla trasformazione è

$J(\rho, \theta) = [(\frac{\partial}{\partial \rho} x, \frac{\partial}{\partial \theta} x),(\frac{\partial}{\partial \rho} y, \frac{\partial}{\partial \theta} y)] = [(a \cos(\theta), -a \rho \sin(\theta)),(b \sin(\theta), b \rho \cos(\theta))]$

Il determinante della matrice Jacobiana vale

$\det(J(\rho, \theta)) = ab \rho \cos^2(\theta) + ab \rho \sin^2(\theta) = ab \rho$

pertanto

$dxdy = |ab \rho| d \rho d \theta = ab \rho d \rho d \theta$

Imponendo la condizione $\frac{x^2}{a^2} + \frac{y^2}{b^2} \le 1$ si ottiene

$\rho^2 \cos^2(\theta) + \rho^2 \sin^2(\theta) \le 1 \implies \rho \in [0, 1]$

Pertanto l’area dell’ellisse vale

$\int_{0}^{2 \pi} \int_{0}^{1} ab \rho d \rho d \theta = \frac{ab}{2} \int_{0}^{2 \pi} [\rho^2]_{0}^{1} d \theta = \frac{ab}{2} \int_{0}^{2 \pi} d \theta = \frac{ab}{2} \cdot 2 \pi = ab \pi$

FINE

Esponenziale di una matrice

Definizione

Data una matrice $A \in \mathbb{R}^{n \times n}$, l’esponenziale di $A$ è definita mediante questo sviluppo in serie

$e^{A} = I + A + \frac{A^2}{2} + \frac{A^3}{3!} + \ldots + \frac{A^n}{n!} + \ldots = \sum_{k=0}^{+\infty} \frac{A^k}{k!}$

dove $A^0 = I$ indica la matrice identità.

Esponenziale di una matrice diagonalizzabile

Se $A \in \mathbb{R}^{n \times n}$ è una matrice diagonalizzabile, il calcolo dell’esponenziale $e^A$ può essere effettuato senza bisogno di ricorrere alla definizione. Detta $T$ la matrice del cambio di coordinate, risulta

$e^A = T e^{\Lambda} T^{-1}$

dove $\Lambda$ è una matrice in forma diagonale se tutti gli autovalori di $A$ sono reali, mentre è in forma diagonale reali a blocchi se $A$ ammette autovalori complessi.

Nel caso di matrici diagonalizzabili dunque è sufficiente calcolare, oltre alla matrice del cambio di coordinate, l’esponenziale p della matrice diagonalizzata, e tale calcolo è relativamente semplice.

Per calcolare $e^{\Lambda}$ si distinguono i casi in cui $\Lambda$ è una matrice in forma diagonale da quello in cui $\Lambda$ è in forma diagonale reale a blocchi.

$A$ ha tutti gli autovalori reali

Se la matrice $A$ ha tutti gli autovalori reali, e questi sono pari a $\lambda_{1}, \lambda_{2}, \ldots, \lambda_n$, ed inoltre se $T$ è la matrice del cambio di coordinate, allora

$A = T \Lambda T^{-1}$

dove

$\Lambda = ((\lambda_{1}, \quad 0, \ldots, 0),(0, \lambda_{2}, \quad \ldots, 0),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(0, \quad 0, \quad \ldots, \quad \lambda_n))$

L’esponenziale di $\Lambda$ è banalmente la matrice ottenuta calcolando gli esponenziali degli elementi sulla diagonale principale

$e^{\Lambda} = ((e^{\lambda_{1}}, \quad 0, \ldots, 0),(0, e^{\lambda_{2}}, \quad \ldots, 0),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),(0, \quad 0, \quad \ldots, \quad e^{\lambda_n}))$

Pertanto, in questo caso, l’esponenziale di $A$ vale

$e^A = T e^{\Lambda} T^{-1}$

$A$ ha almeno un autovalore complesso

$\lambda_i = \sigma_i + i \omega_i$

Se $T$ è la matrice del cambio di coordinate, allora $A = T \Lambda T^{-1}$, dove $\Lambda$ è una matrice in forma diagonale reale a blocchi, della forma

$\Lambda = [(\lambda_1, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(0, \quad \lambda_2, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(\vdots, \quad 0, \quad \ddots, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad 0, \quad \lambda_{r}, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad 0, \quad \sigma_{r+1}, \quad \omega_{r+1}, \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad -\omega_{r+1}, \quad \sigma_{r+1}, \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad 0, \quad \ddots, \quad 0, \quad 0),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad \vdots, \quad \sigma_c, \quad \omega_c),(0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0, \quad -\omega_c, \quad \sigma_c)]$

Ricordando che per ogni autovalore complesso $\lambda_i$ (con parte immaginaria positiva) $\sigma_i$ indica la sua parte reale e $\omega_i$ ($>0$) indica la sua parte immaginaria, l’esponenziale di $\Lambda$ vale

$e^{\Lambda} = [(e^{\lambda_1}, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(0, \quad e^{\lambda_2}, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0),(\vdots, \quad 0, \quad \ddots, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad 0, \quad e^{\lambda_{r}}, \quad 0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad 0, \quad e^{\sigma_{r+1}} \cos(\omega_{r+1}), \quad e^{\sigma_{r+1}} \sin(\omega_{r+1}), \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad -e^{\sigma_{r+1}} \sin(\omega_{r+1}), \quad e^{\sigma_{r+1}} \cos(\omega_{r+1}), \quad 0, \quad \ldots, \quad \vdots),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad 0, \quad \ddots, \quad 0, \quad 0),(\vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \vdots, \quad \ddots, \quad \vdots, \quad e^{\sigma_{c}} \cos(\omega_{c}), \quad e^{\sigma_{c}} \sin(\omega_{c})),(0, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad \ldots, \quad 0, \quad -e^{\sigma_{c}} \sin(\omega_{c}), \quad e^{\sigma_{c}} \cos(\omega_{c}))]$

Una volta calcolata $e^{\Lambda}$ è possibile calcolare anche l’esponenziale di $A$, dato che

$e^A = T e^{\Lambda} T^{-1}$

Rettangolo di area massima

Fra tutti i rettangoli di perimetro $2p$ ($p > 0$) determinare quello di area massma.

Il semiperimetro del rettangolo vale $p$, quindi chiamando con $x$ la base ($0 \le x \le p$) si deduce che l'altezza vale $p – x$. Da notare che se $x = 0 \vee x = p$ il rettangolo degenera in un segmento. La funzione che rappresenta l'area al variare di $x$ è

$f: [0, p] \to \mathbb{R}: x \mapsto x(p-x)$

Per studiare il massimo assoluto di tale funzione si può calcolare la derivata prima.

$f'(x) = p – 2x$

La derivata prima si azzera in $x = \frac{p}{2}$, e dallo studio del segno della derivata prima si nota che in tale punto c'è un massimo.

Dato che $f(0) = f(p) = 0$, e $f(\frac{p}{2}) = \frac{p^2}{4} > 0$, allora in $x = \frac{p}{2}$ la $f$ assume il massimo assoluto.

Quindi il rettangolo di area massima avente perimetro $2p$ è quello che ha base $\frac{p}{2}$ e altezza $\frac{p}{2}$, ovvero il quadrato di perimetro $2p$.

FINE

Spazi di probabilità

Definizione

Se $\Omega$ è un insieme e $\bar{A}$ è l’insieme delle parti di $\Omega$, una probabilità $P$ è una funzione $P: \bar{A} \to [0,1]$ che rispetta queste proprietà

1) $P(\Omega) = 1$

2) Se $\{A_i\}_{i=1}^{+\infty}$ sono elementi di $\bar{A}$ a due a due disgiunti, cioè $A_i \cap A_j = \emptyset$, per $i \ne j$, allora

$P(\bigcup_{i=1}^{+\infty} A_i) = \sum_{i=1}^{+\infty} P(A_i)$

Una terna $(\Omega, \bar{A}, P)$ è uno spazio di probabilità.

Caso particolare: equiprobabilità

Se $\Omega$ ha cardinalità finitia, pari a $n$, e gli eventi sono equiprobabili, il calcolo della probabilità di un evento $A \in \bar{A}$ si riduce a

$P(A) = \frac{"card"(A)}{"card"(\Omega)} = \frac{"card"(A)}{n}$

che intuitivamente equivale a $\frac{"numero casi favorevoli"}{"numero casi possibili"}$.

Esempio: calcolare la probabilità che, lanciando un dado, esca $1$. Vale $\Omega = \{1, 2, 3, 4, 5, 6\}$, si suppongono gli eventi equiprobabili, cioè $P(\{1\}) = P(\{2\}) = P(\{3\}) = P(\{4\}) = P(\{5\}) = P(\{6\}) = p$. Dato che $P(\Omega) = 1$, $\Omega = \{1\} \cup \{2\} \cup \{3\} \cup \{4\} \cup \{5\} \cup \{6\}$, e che questi insiemi sono disgiunti, allora

$1 = P(\Omega) = P(\{1\} \cup \{2\} \cup \{3\} \cup \{4\} \cup \{5\} \cup \{6\}) = P(\{1\}) + P(\{2\}) + P(\{3\}) + P(\{4\}) + P(\{5\}) + P(\{6\} )= 6p$

Dato che $6p = 1$, allora $p = \frac{1}{6}$, quindi la probabilità che esca $1$ (così come quella che un altro numero compreso fra $2$ e $6$) è $\frac{1}{6}$. E infatti i casi possibili sono $6$, quelli favorevoli solo $1$.

Esempio: calcolare la probabilità di fare terno al lotto (giocando cinque numeri). I casi possibili sono tutte le possibili cinquine che si possono ottenere estraendo numeri compresi fra $1$ e $90$, cioè $C_{90, 5} = ((90),(5)) = \frac{90!}{5! 85!}$. I casi favorevoli sono tutti i casi in cui esce una cinquina contenente i tre numeri giocati. Dato che tre numeri sono fissati i casi favorevoli sono $C_{87, 2} = ((87),(2)) = \frac{87!}{2! 85!}$. La probabiliyà richiesta quindi vale

$\frac{C_{87, 2}}{C_{90, 5}} = \frac{5! 87!}{2 \cdot 90!}$

Proprietà

$P(A^c) = 1 – P(A)$

$P(A) = 1 – P(A^c)$

$P(\emptyset) = 0$ (dato che $\emptyset = \Omega^c$ e $P(\Omega) = 1$)

$P(\bigcup_{i=1}^{+\infty} A_i) = 1 – P(\bigcap_{i=1}^{+\infty} A_i^c)$

$P(B) = P(B \cap A) + P(B \cap A^c)$

Se $A \subseteq B$, allora

$P(A) \le P(B)$

Se $A$ e $B$ sono due insiemi disgiunti, cioè $A \cap B = \emptyset$, allora

$P(A \cup B) = P(A) + P(B)$

Se invece $A$ e $B$ non sono disgiunti vale

$P(A \cup B) = P(A) + P(B) – P(A \cap B)$

$P(A \cup B) = P(A) + P(B \cap A^c)$

Nota

$P(A \cup B)$ indica la probabilità che si verifichi almeno uno fra gli eventi $A$ e $B$

$P(A \cap B)$ indica la probabilità che gli eventi $A$ e $B$ si verifichino entrambi

$P(A^c)$ indica la probabilità che l’evento $A$ non si verifichi

Esempio: calcolare la probabilità di ottenere almeno un $6$ lanciando tre volte un dado. Sia $A_i$ l’evento "al lancio $i$-esimo esce $6$", quindi la probabilità richiesta vale

$P(A_1 \cup A_2 \cup A_3)$

ed equivale a

$1 – P(A_1^c \cap A_2^c \cap A_3^c)$

Il complementare di $A_i$ è $A_i^c$ ed indica l’evento "al lancio $i$-esimo non esce $6$", pertanto l’evento $A_1^c \cap A_2^c \cap A_3^c$ equivale a "in tre lanci non esce mai $6$". In quest’ultimo evento i casi possibili sono $6 \cdot 6 \cdot 6 = 6^3$, quelli favorevoli sono $5 \cdot 5 \cdot 5 = 5^3$, quindi

$P(A_1^c \cap A_2^c \cap A_3^c) = (\frac{5}{6})^3$

pertanto la probabilità richiesta vale

$1 – P(A_1^c \cap A_2^c \cap A_3^c) = 1 – (\frac{5}{6})^3$

Studio della funzione $f(x) = |x^2 – 2x| e^x$

Studiare il grafico della seguente funzione reale di variabile reale

$f(x) = |x^2 – 2x| e^x$

Il dominio massimale della funzione è $\mathbb{R}$. Ricordando la definizione di valore assoluto si nota che

$f(x) = \{((x^2 – 2x)e^x, "se " x \le 0 \vee x \ge 2),((2x-x^2) e^x, "altrimenti"):}$

La $f$ è data dalla composizione di funzioni continue, pertanto è continua nel suo dominio. Dato che $f(x) \ne f(-x)$ e $f(x) \ne -f(-x)$ la funzione non è né pari né dispari.

$x=0 \implies f(0) = 0$

$f(x) = 0 \implies x = 0 \vee x=2$

pertanto i punti di intersezione fra il grafico della funzione e gli assi cartesiani sono $(0,0)$ e $(2,0)$. Visto che l’esponenziale e il valore assoluto sono non negativi, la funzione è non negativa nel suo dominio.

$\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} (x^2 – 2x) e^x = \lim_{x \to +\infty} x(x-2) e^x = +\infty$

$\lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x^2 – 2x}{x} e^x = \lim_{x \to +\infty} (x-2) e^x = +\infty$

pertanto, per $x \to +\infty$, non ci sono asintoti orizzontali né obliqui.

$\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{x^2 – 2x}{e^{-x}}$

Applicando due volte il teorema di de l’Hopital si ottiene

$\lim_{x \to -\infty} \frac{2x-2}{-e^{-x}} = \lim_{x \to -\infty} \frac{2}{e^{-x}} = 0$

pertanto la retta di equazione $y=0$ è un asintoto orizzontale sinistro per il grafico della funzione in questione. La derivata prima vale

$f'(x) = \{(e^x (x^2 – 2), "se " x < 0 \vee x > 2),(e^x (2 – x^2), "se " 0 < x < 2):}$

$\lim_{x \to 0^{-}} f'(x) = \lim_{x \to 0^{-}} e^x (x^2 – 2) = -2$

$\lim_{x \to 0^{+}} f'(x) = \lim_{x \to 0^{+}} e^x (2 – x^2) = 2$

Pertanto in $0$ c’è un punto angoloso, quindi $(0,0)$ è un punto di non derivabilità.

$\lim_{x \to 2^{-}} f'(x) = \lim_{x \to 2^{-}} e^x (2 – x^2) = -2 e^2$

$\lim_{x \to 2^{+}} f'(x) = \lim_{x \to 2^{+}} e^x (x^2 -2) = 2 e^2$

Anche in $2$ c’è un punto angoloso, pertanto anche $(2,0)$ è un punto di non derivabilità. La derivata prima si azzera in $x = \pm \sqrt{2}$. Per determinare il segno della derivata prima occorre studiare $f'(x) \ge 0$, che equivale a

$\{(x^2 – 2 \ge 0),(x < 0 \vee x > 2):} \quad \vee \quad \{(2 – x^2 \ge 0),(0 < x <2 ):} \implies (x < -\sqrt{2} \vee x > 2) \vee (0 < x < \sqrt{2})$

Dallo studio del segno della derivata prima si deduce che in $x=0$ e $x=2$ ci sono dei minimi, mentre in $x=\pm \sqrt{2}$ ci sono dei massimi. La derivata seconda vale

$f”(x) = \{(e^x (x^2 + 2x – 2), "se " x < 0 \vee x > 2),(e^x (2 – 2x – x^2), "se " 0 < x < 2):}$

La derivata seconda si azzera per

$\{(x^2 + 2x – 2=0),(x < 0 \vee x > 2):} \quad \vee \quad \{(2 – 2x – x^2 = 0),(0 < x < 2):}$

ovvero per $x=1 \vee x = -3$. Il segno della derivata secodna viene determinato studianto $f”(x) \ge 0$, ovvero

$\{(x^2 + 2x – 2 \ge 0),(x < 0 \vee x > 2):} \quad \vee \quad \{(2 – 2x – x^2 \ge 0),(0 < x < 2):}$

che equivale a

$\{(x < -3 \vee x > 1),(x < 0 \vee x > 2):} \quad \vee \quad \{(-3 < x < 1),(0 < x < 2):}$

Quindi la funzione è convessa se $(x < -3 \vee x > 2) \vee (0 < x < 1)$, concava altrimenti. Questo è il grafico della funzione

Quindi l’immagine della funzione è $\{x \in \mathbb{R}: x \ge 0\}$.

FINE

Probabilità condizionale e indipendenza

Definizione

Dati due eventi $A, B$, si definisce probabilità condizionale di $B$ rispetto ad $A$, e si indica con $P(B | A)$, la quantità

$P(B | A) = \frac{P(B \cap A)}{P(A)}$

Intuitivamente $P(B | A)$ indica la probabilità che si verifichi $B$ sapendo che si è verificato $A$.

Probabilità dell’intersezione

Dati due eventi $A, B$, sfruttando la probabilità condizionale, la probabilità che $A$ e $B$ si verifichino entrambe vale

$P(A \cap B) = P(B | A) P(A)$ oppure $P(A \cap B) = P(A | B) P(B)$

Esempio: da un’urna con $10$ palline numerate da $1$ a $10$ si estraggono due palline senza rimpiazzo. Calcolare la probabilità che entrambe le palline abbiano numeri pari.

Sia $A_i$ l’evento "all’$i$-esima pallina estratta corrisponde un numero pari". Si vuole calcolare $P(A_1 \cap A_2) = P(A_2 | A_1) P(A_1)$

$P(A_1) = \frac{1}{2}$, dato che inizialmente ci sono tanti numeri pari quanti numeri dispari, e che sono tutti equiprobabili

$P(A_2 | A_1) = \frac{4}{9}$, dato che, se è stato estratto un numero pari, i numeri pari rimasti sono $4$, mentre le palline totali nell’urna sono $9$.

Quindi $P(A_1 \cap A_2) = \frac{1}{2} \cdot \frac{4}{9} = \frac{2}{9}$.

Teorema di Bayes

Sia $(\Omega, \bar{A}, P)$ uno spazio di probabilità, e siano $A_1, A_2, \ldots, A_n \in \bar{A}$ eventi disgiunti tali che $A_1 \cup A_2 \cup \ldots \cup A_n = \Omega$. Dato un evento $B \in \bar{A}$ risulta

$P(B) = \sum_{i=1}^n P(A_i) P(B | A_i)$

ed inoltre

$P(A_k | B) = \frac{P(A_k \cap B)}{P(B)} = \frac{P(A_k) P(B | A_k)}{\sum_{i=1}^n P(A_i) P(B | A_i)}$, per ogni $k=1, 2, \ldots, n$ (teorema di Bayes)

Esempio: tre urne contengono $10$ palline ciascuna. Le palline nell’urna A sono contrassegnate con i numeri che vanno dall’1 al 10, quelle nell’urna B con i numeri che vanno dal 4 al 13, mentre quelle nell’urna C sono numerate dal 6 al 15. Calcolare la probabilità che si sia scelta l’urna A, sapendo che è stata estratta una pallina contrassegnata con il numero 5.

Indicando con $A$, $B$, $C$, gli eventi "è stata scelta l’urna A/B/C", rispettivamente," e con $X_5$ l’evento "è stata estratta una pallina contrassegnata con il 5", la probabilità richiesta vale

$P(A | X_5) = \frac{P(X_5 \cap A)}{P(X_5)} = \frac{P(X_5 | A) P(A)}{P(X_5 | A) P(A) + P(X_5 | B) P(B) + P(X_5 | C) P(C)}$

Considerando che l’urna $C$ non contiene palline numerate con $5$ la probabilità da calcolare diventa

$P(A | X_5) = \frac{\frac{1}{10} \cdot \frac{1}{3}}{\frac{1}{10} \cdot \frac{1}{3} + \frac{1}{10} \cdot \frac{1}{3}} = \frac{1}{2}$

Eventi indipendenti

Due eventi $A$ e $B$ si dicono indipendenti se e solo se $P(A \cap B) = P(A) P(B)$.

Se $A$ e $B$ sono indipendenti allora $P(B | A) = P(B)$, cioè il verificarsi di $A$ non dà informazioni sul verificarsi di $B$.

Esempio: calcolare la probabilità che lanciando per due volte una moneta (non truccata) si ottenga per due volte testa. Sia $A_i$ l’evento "all’$i$-esimo lancio è uscita testa", ciò che si vuole calcolare è $P(A_1 \cap A_2)$. I casi possibili sono quattro (testa-testa, testa-croce, croce-testa, croce-croce) mentre i casi favorevoli sono solo uno (testa-testa), quindi $P(A_1 \cap A_2) = \frac{1}{4}$. D’altra parte $P(A_1) = P(A_2) = \frac{1}{2}$, quindi $P(A_1 \cap A_2) = P(A_1) P(A_2)$ di conseguenza gli eventi $A_1$ e $A_2$ sono indipendenti (e infatti l’esito del primo lancio non può influenzare l’esito del secondo).

$f(x) = e^x root{3}{x^2}$

Studiare il grafico della seguente funzione reale di variabile reale

$f(x) = e^x \root{3}{x^2}$

Il dominio massimale della funzione è $\mathbb{R}$, dato che un esponenziale è definito laddove è definito l’esponente, e una radice di indice dispari è definita laddove è definito il radicando. La $f$ è data dalla composizione di funzioni continue, pertanto nel suo dominio è continua.

La funzione in questione non è né pari né dispari, infatti $f(-x) \ne f(x)$ e $f(-x) \ne -f(x)$.

$x = 0 \implies f(0) = 0$

$f(x) = 0 \implies x = 0$

Pertanto il grafico della funzione interseca gli assi cartesiani solo nel punto $(0,0)$. La funzione è positiva (o al più uguale a zero) per:

$f(x) \ge 0 \implies e^x \root{3}{x^2} \ge 0 \implies \root{3}{x^2} \ge 0 \implies x^2 \ge 0 \forall x \in \mathbb{R}$

Pertanto la $f$ è non negativa in tutto il suo dominio.

$\lim_{x \to +\infty} e^x \root{3}{x^2} = +\infty$

$\lim_{x \to -\infty} e^x \root{3}{x^2} = \lim_{x \to -\infty} \frac{\root{3}{x^2}}{e^{-x}}$

Applicando il teorema di de l’Hopital per risolvere quest’ultimo limite si ottiene

$\lim_{x \to -\infty} \frac{2}{3} \frac{e^x}{\root{3}{x}} = 0$

Pertanto la retta di equazione $y=0$ è un asintoto orizzontale sinistro, non si sono invece asintoti orizzontali destri. Si può quindi cercare un eventuale asintoto obliquo destro

$\lim_{x \to +\infty} \frac{e^x \root{x}{x^2}}{x} = \lim_{x \to +\infty} \frac{e^x}{\root{3}{x}}$

Applicando il teorema di de l’Hopital si ottiene

$\lim_{x \to +\infty} 3 e^x \root{3}{x^2} = +\infty$

quindi non ci sono asintoti obliqui. La derivata vale

$f'(x) = e^x \root{3}{x^2} + e^x \frac{2}{3 \root{3}{x}} = e^x (\root{3}{x^2} + \frac{2}{3 \root{3}{x}})$

La derivata prima calcolata in $x=0$ vale

$\lim_{h \to 0} \frac{f(0+h) – f(0)}{h} = \lim_{h \to 0} \frac{e^h \root{3}{h^2}}{h} = \lim_{h \to 0} \frac{e^h}{\root{3}{h}}$

Dato che

$\lim_{h \to 0^+} \frac{e^h}{\root{3}{h}} = +\infty$

$\lim_{h \to 0^-} \frac{e^h}{\root{3}{h}} = -\infty$

si deduce che in $x=0$ c’è una cuspide, pertanto $(0,0)$ non è un punto di derivabilità. La derivata prima si annulla per

$f'(x) = 0 \implies \root{3}{x^2} = -\frac{2}{3 \root{3}{x}} = x = -\frac{2}{3}$

Dallo studio del segno della derivata prima, si nota che la funzione è crescente per $x \in (-\infty, -\frac{2}{3}) \cup (0, +\infty)$, mentre è decrescente per $x \in (-\frac{2}{3}, 0)$. Pertanto in $x = -\frac{2}{3}$ c’è un massimo relativo. La derivata seconda invece vale

$f”(x) = e^x (\root{3}{x^2} + \frac{2}{3 \root{3}{x}}) + e^x (\frac{2}{3 \root{3}{x}} + \frac{2}{3} (-\frac{1}{3}) \frac{1}{\root{3}{x^4}}) = e^x (\frac{9x^2 + 12x – 2}{9 \root{3}{x^4}})$

La derivata seconda si annulla per

$9x^2 + 12x – 2 = 0 \implies x_{1,2} = \frac{-6 \pm \sqrt{36+18}}{9}$

da cui

$x_1 = \frac{-2-\sqrt{6}}{3} \quad x_2 = \frac{-2+\sqrt{6}}{3}$

Pertanto $x_1$ e $x_2$ sono due punti di flesso a tangente obliqua. Dato che il denominatore della derivata seconda è sempre positivo, si nota che la funzione è concava per $x \in (\frac{-2-\sqrt{6}}{3}, 0) \cup (0, \frac{-2+\sqrt{6}}{3})$ ed è invece convessa per $x \in (-\infty, \frac{-2-\sqrt{6}}{3}) \cup (\frac{-2+\sqrt{6}}{3}, +\infty)$.

Questo è il grafico della funzione

Dunque la funzione ha un minimo assoluto in $(0,0)$, e l’immagine è

$\{x \in \mathbb{R}: x \ge 0\}$

FINE

Studio di funzione esponenziale $f(x) = x e^{-frac{1}{x}}$

Studiare il grafico della seguente funzione reale di variabile reale

$f(x) = x e^{-\frac{1}{x}}$

Il prodotto fra due termini è definito laddove sono definiti i due fattori, allo stesso modo un esponenziale è definito laddove è definito l’esponente, pertanto il dominio massimale di questa funzione è

$\{x \in \mathbb{R}: x \ne 0\}$

Dato che $f(x) \ne f(-x)$ e allo stesso tempo $f(x) \ne -f(-x)$ la funzione non è né pari né dispari. Visto che $f$ è data dalla composizione di funzioni continue, allora nel suo dominio è continua.

$f(x) = o \quad \implies \quad x=0$, considerando che tale punto non appartiene al dominio, si deduce che non ci sono intersezioni fra il grafico della funzione e gli assi cartesiani.

$e^{-\frac{1}{x}} > 0 \quad \forall x \in \mathbb{R} \setminus \{0\}$

pertanto la funzione è positiva se $x>0$ e negativa se $x < 0$.

$\lim_{x \to 0^{+}}x e^{-\frac{1}{x}} = 0 \cdot e^{-\infty} = 0$

$\lim_{x \to 0^{-}} = x e^{-\frac{1}{x}} = \lim_{x \to 0^{-}} \frac{e^{-\frac{1}{x}}}{\frac{1}{x}}$

Sfruttando il teorema di de l’Hopital si ottiene

$\lim_{x \to 0^{-}} \frac{e^{-\frac{1}{x}}}{\frac{1}{x}} = \lim_{x \to 0^{-}} \frac{e^{-\frac{1}{x}} \frac{1}{x^2}}{\frac{1}{x^2}} = \lim_{x \to 0^{-}} e^{-\frac{1}{x}} = -\infty$

Pertanto il grafico della funzione ammette come asintoto verticale sinistro la retta di equazione $x=0$.

$\lim_{x \to +\infty} x e^{-\frac{1}{x}} = +\infty$

$\lim_{x \to -\infty} x e^{-\frac{1}{x}} = -\infty$

quindi non ci sono asintoti orizzontali.

$m = \lim_{x \to \pm \infty} \frac{x e^{-\frac{1}{x}}}{x} = 1$

$q = \lim_{x \to \pm \infty} x e^{-\frac{1}{x}} – x = \lim_{x \to \pm \infty} x (e^{-\frac{1}{x}} – 1) = \lim_{x \to \pm \infty} – \frac{e^{-\frac{1}{x}} – 1}{-\frac{1}{x}} = -1$

dove all’ultimo passaggio è stato sfruttato il limite notevole

$\lim_{t \to 0} \frac{e^t – 1}{t} = 1$

Dai calcoli precedenti si nota che la funzione ammette un asintoto obliquo di equazione $y = x – 1$.

La derivata priam dela funzione vale

$f'(x) = e^{-\frac{1}{x}} + x e^{-\frac{1}{x}} \cdot \frac{1}{x^2} = e^{-\frac{1}{x}} (1 + \frac{1}{x})$

La $f$ è data dalla composizione continue e derivabili, pertanto nel suo dominio è continua e derivabile.

$f'(x) = o \implies 1 + \frac{1}{x} = 0 \implies x = -1$

$f'(x) > 0 \implies 1 + \frac{1}{x} > 0 \implies x < -1$

Dato che in $-1$ la funzione passa da essere crescente a decrescente, considerando che $f(-1) = -e$, si deduce che il punto $(-1, -e)$ è un minimo. Visto che $-e < -1 -1$ si nota che il minimo si trova sotto all’asintoto obliquo, ovvero nella parte di piano $y \le x – 1$.

La derivata seconda della funzione vale

$f”(x) = e^{-\frac{1}{x}} \frac{1}{x^2} + (-\frac{1}{x^2}) e^{-\frac{1}{x}} + \frac{1}{x^3} e^{-\frac{1}{x}} = \frac{1}{x^3} e^{-\frac{1}{x}}$

La derivata seconda non si annulla mai, pertanto non ci sono punti di flesso a tangente obliqua. Dal segno della derivata seconda si nota che la funzione è concava per $x < 0$ e convessa per $x > 0$. Dai calcoli svolti si può concludere che non ci sono intersezioni fra il grafico della funzione e l’asintoto obliquo.

L’immagine della funzione coincide con l’insieme

$(-\infty, -e] \cup (0, +\infty)$

Questo è il grafico della funzione

FINE

Variabili aleatorie discrete scalari

Definizione

Se $(\Omega, \bar{A}, P)$ è uno spazio di probabilità, una variabile aleatoria (scalare) è una funzione $X: \Omega \to \mathbb{R}$ tale che

$\{\omega \in \Omega: X(\omega) \le t\} \in \bar{A}$ per ogni $t \in \mathbb{R}$

Una variabile aleatoria discreta scalare è una variabile aleatoria scalare che può assumere un numero finito o, al più, un’infinità numerabile di valori (senza punti di accumulazione).

Esempio: supponiamo di avere un dado (a sei facce) non truccato. Se definiamo

$X = \{(1, \quad "se esce " 1),(2, \quad "se esce " 2),(3, \quad "se esce " 3),(4, \quad "se esce " 4),(5, \quad "se esce " 5),(6, \quad "se esce " 6):}$

allora $X$ è una variabile aleatoria discreta.

Proprietà

Se $(\Omega, \bar{A}, P)$ è uno spazio di probabilità e $X: \Omega \to \mathbb{R}$ è una variabile aleatoria, allora

$\{\omega \in \Omega: X(\omega) > t \} \in \bar{A}$ per ogni $t \in \mathbb{R}$

$\{\omega \in \Omega: X(\omega) < t\} \in \bar{A}$ per ogni $t \in \mathbb{R}$

$\{\omega \in \Omega: X(\omega) \ge t\} \in \bar{A}$ per ogni $t \in \mathbb{R}$

$\{\omega \in \Omega: X(\omega) = t \} \in \bar{A}$ per ogni $t \in \mathbb{R}$

Per semplicità notazionale, si pone

$\{X \in A\} =_{"def"} \{\omega \in \Omega: X(\omega) \in A\}$

$\{X < t\} =_{"def"} \{\omega \in \Omega: X(\omega) < t\}$

La probabilità di eventi del tipo $\{X \in A\}$ equivale a

$P(\{X \in A\}) = \sum_{x_k \in A} P(\{X = x_k\})$

Esempio: calcolare la probabilità che, lanciando un dado non truccato, esca un numero pari. Sia $X$ la variabile aleatoria discerta definita nell’esempio precedente, si richiede di calcolare $P(\{X \in A\})$, dove $A = \{2, 4, 6\}$. Data l’ipotesi di equiprobabilità vale

$P(\{X = 1\}) = P(\{X = 2\}) = P(\{X = 3\}) = P(\{X = 4\}) = P(\{X = 5\}) = P(\{X = 6\}) = \frac{1}{6}$

quindi

$P(\{X \in A\}) = \sum_{x_k \in A} P(\{X = x_k\}) = P(\{X = 1\}) + P(\{X = 2\}) + P(\{X = 3\}) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{1}{2}$

Densità di probabilità discreta

Se $X$ è una variabile aleatoria discreta, la funzione

$p(x_k) = P(\{X = x_k\})$

si chiama funzione di densità di probabilità discreta. Se $x$ non è uno dei valori assunti da $X$, vale $p(x) = P(\{X = x\}) = 0$.

Proprietà

– Una densità di probabilità discreta è una funzione $p: \mathbb{R} \to [0,1]$

– Vale $p(x) > 0$ in (al più) un’infinità numerabile di punti, $x_1, x_2, \ldots, x_k, \ldots$, e $p(x) = 0$ altrove

– Risulta $\sum_{k=1}^{+\infty} p(x_k) = 1$, se $\{x_k\}_{k=1}^{+\infty}$ è l’insieme di tutti e soli i valori che la variabile aleatoria può assumere

Esempio: sia $X$ la variabile aleatoria definita nei due esempi precedenti. Data l’ipotesi di equiprobabilità, la sua densità di probabilità vale

$p(x) = \{(\frac{1}{6}, \quad "se " x \in \{1, 2, 3, 4, 5, 6\}),(0, \quad "altrimenti"):}$

Esempio: supponiamo di avere una moneta truccata, in modo che la probabilità che esca testa valga $p$, la probabilità che esca croce valga $1 – p$, e supponiamo di lanciarla $n$ volte. La variabile aleatoria $X = "numero di volte che esce testa"$ è una variabile aleatoria discreta, e la sua densità di probabilità vale

$p(k) = \{(((n),(k)) p^k (1-p)^{n-k}, \quad "se " k \in \{0, 1, \ldots, n\}),(0, \quad "altrimenti"):}$

$p(k)$ indica la probabilità che esca testa per $k$ volte su $n$ lanci. La probabilità che esca testa $k$ volte è $p^k$ (sono eventi indipendenti, ognuno con probabilità $p$), la probabilità che esca croce nei restanti casi (che sono $n-k$) è $(1-p)^{n-k}$ (sono eventi indipendenti, ognuno con probabilità $1-p$), i possibili modi con cui possono accadere questi eventi sono $C_{n,k} = ((n),(k))$, pertanto la probabilità che escano $k$ teste su $n$ lanci è proprio $((n),(k)) p^k (1-p)^{n-k}$. Notare che

$\sum_{k=0}^{+\infty} p(k) = \sum_{k=0}^n ((n),(k)) p^k (1-p)^{n-k} = (p + 1 – p)^n = 1^n = 1$ (binomio di Newton)

Quando una variabile aleatoria $X$ segue questa densità di probabilità si dice che è distribuita come una binomiale $B(n, p)$, e si scrive $X \sim B(n, p)$.

Densità di probabilità discrete notevoli

Legge binomiale $B(n, p)$ ($n \in \mathbb{N}$, $p \in [0,1]$)

$p(k) = \{(((n),(k)) p^k (1-p)^{n-k}, \quad "se " k \in \{0, 1, \ldots, n\}),(0, \quad "altrimenti"):}$

Densità ipergeometrica

$p(k) = \{(\frac{((b),(k)) \cdot ((r),(n-k))}{((b+r),(n))}, \quad "se " k \in \{0, 1, \ldots, "min" \{b, n\}\}),(0, \quad "altrimenti"):}$

Densità geometrica di parametro $p$ ($p \in [0,1]$)

$p(k) = \{(p (1-p)^{k-1}, \quad "se " k \in \mathbb{N} \setminus \{0\}),(0, \quad "altrimenti"):}$

Densità di Poisson ($\lambda \in \mathbb{R}^+$)

$p(k) = \{(e^{-\lambda} \frac{\lambda^k}{k!}, \quad "se " k \in \mathbb{N}),(0, \quad "altrimenti"):}$

Densità discreta uniforme ($A$ è un insieme non vuoto con cardinalità finita)

$p(k) = \{(\frac{1}{"card"(A)}, \quad "se " k \in A),(0, \quad "altrimenti"):}$

Variabili aleatorie discrete vettoriali

Definizione

Se $(\Omega, \bar{A}, P)$ è uno spazio di probabilità, una variabile aleatoria vettoriale $X$ è una funzione $X: \Omega \to \mathbb{R}^n$

$X(\omega) = (X_1(\omega), X_2(\omega), \ldots, X_n(\omega))$

dove ogni componente è una variabile aleatoria scalare. Dunque una variabile aleatoria discreta vettoriale è un vettore di variabili aleatorie scalari.

Densità di probabilità congiunta (discreta)

Data un variabile aleatoria discreta vettoriale $X$ (a $n$ dimensioni), fissato $x = (x_1, x_2, \ldots, x_n) \in \mathbb{R}^n$, la densità di probabilità congiunta di $X$ è definita come

$p(x) = P(\{X = x\}) = P(\{X_1 = x_1\} \cap \{X_2 = x_2\} \cap \ldots \cap \{X_n = x_n\})$

Proprietà

1) $p(x) \in [0,1]$ per ogni $x \in \mathbb{R}^n$

2) $p(x) > 0$ solo in (al più) un’infinità numerabile di punti, $x^{(1)}, x^{(2)}, \ldots, x^{(k)}, \ldots$, e $p(x) = 0$ altrove

3) $\sum_{k} p(x^{(k)}) = 1$, se $x^{(1)}, x^{(2)}, \ldots, x^{(k)}, \ldots$ sono tutti e soli i valori che la $X$ può assumere (notare che $x^{(k)}$ è un vettore di $\mathbb{R}^n$, cioè $x^{(k)} = (x_1^{(k)}, x_2^{(k)}, \ldots, x_n^{(k)})$)

Densità di probabilità marginali

Data una variabile aleatoria vettoriale $X = (X_1, X_2, \ldots, X_n)$, le densità di probabilità delle componenti $X_i$ si chiamano densità di probabilità marginali di $X$. Dalla densità di probabilità congiunta di $X$ si può sempre risalire alle marginali, non è sempre vero il viceversa.

Caso $n=2$

Sia $X = (X_1, X_2)$ è una variabile aleatoria vettoriale, e sia $p$ la densità di probabilità congiunta. Se $x^{(1)}, x^{(2)}, \ldots, x^{(k)}, \ldots$ sono tutti e soli i valori che può assumere $x$, dove $x^{(k)} = (x_1^{(k)}, x_2^{(k)}$, le due marginali valgono

$p_1(z) = \sum_{k} p(z, x_2^{(k)})$

$p_2(z) = \sum_{k} p(x_1^{(k)}, z)$

Variabili aleatorie indipendenti

Si dice che $n$ variabili aleatorie $X_1, X_2, \ldots, X_n$ sono indipendenti se e solo se

$P(\{X_1 \in A_1, X_2 \in A_2, \ldots, X_n \in A_n\}) = P(\{X_1 \in A_1\}) \cdot P(\{X_2 \in A_2\}) \cdot \ldots \cdot P(\{X_n \in A_n\})$

per ogni $A_1, A_2, \ldots, A_n \subseteq \mathbb{R}$.

Densità di probabilità congiunta e marginale

Se $X = (X_1, X_2, \ldots, X_n)$, e le variabili $X_1, X_2, \ldots, X_n$ sono indipendenti, allora la densità di probabilità congiunta di $X$ è uguale al prodotto delle densità di probabilità marginali

$p(x) = p_1(x_1) \cdot p_2(x_2) \cdot \ldots \cdot p_n(x_n)$

dove $x = (x_1, x_2, \ldots, x_n)$. Nel caso di variabili aleatorie indipendenti si può passare dalla congiunta alle marginali e dalle marginali alla congiunta.

Valore atteso, varianza, covarianza (caso discreto)

Valore atteso

Definizione

Data una variabile aleatoria discreta $X$ che può assumere i valori $x_1, x_2, \ldots, x_k, \ldots$, si dice che $X$ ha speranza matematica finita se e solo se

$\sum_{k} |x_k| p(x_k) < +\infty$ ($p$ è la densità di probabilità di $X$)

e in tal caso si chiama valore atteso di $X$ la quantità

$E[X] = \sum_{k} x_k p(x_k)$

Esempio: dato un dado non truccato, sia $X = "numero uscito dopo un lancio"$. Calcolare il valore atteso di $X$. VIsta l’ipotesi di equiprobabilità, la densità di probabilità di $X$ vale

$p(k) = \{(\frac{1}{6}, \quad "se " k \in \{1, 2, 3, 4, 5, 6\}),(0, \quad "altrimenti"):}$

Quindi il valore atteso di $X$ vale

$E[X] = \sum_{k=1}^6 k p(k) = 1 \cdot \frac{1}{6} + 2 \frac{1}{6} + 3 \frac{1}{6} + 4 \frac{1}{6} + 5 \frac{1}{6} + 6 \frac{1}{6} = \frac{7}{2}$

Caso vettoriale

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale, il suo valore atteso è il vettore dei valori attesi delle componenti, cioè

$E[X] = (E[X_1], E[X_2], \ldots, E[X_n])$

Proprietà del valore atteso

– Linearità

$E[X + Y] = E[X] + E[Y]$

$E[\alpha X] = \alpha E[X]$, per ogni $\alpha \in \mathbb{R}$

– Valore atteso di una funzione di variabili aleatorie

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale che può assumere i valori $x^{(1)}, x^{(2)}, \ldots, x^{(k)}, \ldots$, se $p$ è la sua densità di probabilità congiunta e se $\phi$ è una funzione $\phi: \mathbb{R}^n \to \mathbb{R}$, allora il valore atteso di $\phi(X)$ vale

$E[\phi(X)] = \sum_{k} \phi(x^{(k)}) p(x^{(k)})$

supposto che $\sum_{k} |\phi(x^{(k)})| p(x^{(k)}) < +\infty$.

– Valore atteso di un prodotto: se $X$ e $Y$ sono variabili aleatorie indipendenti, allora

$E[X Y] = E[X] E[Y]$

Varianza

Se $X$ è una variabile aleatoria scalare, si definisce varianza di $X$ la quantità

$"Var"(X) = \sigma_X^2 = E[(X – E[X])^2]$

Se $X$ è una variabile aleatoria discreta con densità di probabilità $p(\cdot)$, e $x_1, x_2, \ldots, x_k, \ldots$ sono tutti e soli i valori che può assumere, allora

$"Var"(X) = \sum_{k} (x_k – E[X])^2 p(x_k)$

La quantità $\sigma_X = \sqrt{"Var"(X)}$ si chiama deviazione standard.

Disuguaglianza di Chebyshev

Fissato $\eta \in \mathbb{R}^+$, risulta

$P(\{|X – E[X]| > \eta\}) \le \frac{"Var"(X)}{\eta^2}$

Proprietà della varianza

$"Var"(X) = E[X^2] – (E[X])^2$

$"Var"(\alpha X) = \alpha^2 "Var"(X)$, per ogni $\alpha \in \mathbb{R}$

$"Var"(\alpha + X) = "Var"(X)$, per ogni $\alpha \in \mathbb{R}$

Covarianza

Date due variabili aleatorie scalari $X$ e $Y$, si definisce covarianza, fra $X$ e $Y$, la quantità

$"Cov"(X, Y) = E[(X – E[X]) \cdot (Y – E[Y])]$

Proprietà

$"Cov"(X, Y) = E[X Y] – E[X] E[Y]$

$"Var"(X + Y) = "Var"(X) + 2 "Cov"(X, Y) + "Var"(Y)$

$"Cov"(X, Y) = "Cov"(Y, X)$

Coefficiente di correlazione

Date due variabili aleatorie scalari $X$ e $Y$, si definisce coefficiente di correlazione la quantità

$\rho_{X, Y} = \frac{"Cov"(X, Y)}{\sqrt{"Var"(X)} \cdot \sqrt{"Var"(Y)}}$

Due variabili aleatorie si dicono scorrelate se e solo se $\rho_{X, Y} = 0$, cioè se e solo se $"Cov"(X, Y) = 0$, o equivalentemente $E[X Y] = E[X] E[Y]$

Nota: due variabili aleatorie indipendenti sono anche scorrelate, non è vero, in generale, il viceversa.

Matrice di covarianza

Se $X = ((X_1),(X_2),(\vdots),(X_n))$ è una variabile aleatoria vettoriale, si definisce matrice di covarianza di $X$

$\Sigma_X = E[(X – E[X]) \cdot (X – E[X])^T]$ (i vettori sono intesi come colonne)

La matrice di covarianza di $X$ equivale a

$\Sigma_X = (("Var"(X_1), \quad "Cov"(X_1, X_2), \quad \ldots, \quad "Cov"(X_1, X_n)),("Cov"(X_2, X_1), \quad "Var"(X_2), \quad \ldots, \quad "Cov"(X_2, X_n)),(\vdots, \quad \vdots, \quad \ddots, \quad \vdots),("Cov"(X_n, X_1), \quad "Cov"(X_n, X_2), \quad \ldots, \quad "Var"(X_n)))$

Si nota che l’elemento di $\Sigma_X$ di posto $ij$ vale

$\Sigma_{X_{ij}} = \{("Var"(X_i), \quad "se " i = j),("Cov"(X_i, X_j), \quad "se " i \ne j):}$

Proprietà

La matrice di covarianza è simmetrica

$\Sigma_X = \Sigma_X^T$

dato che $"Cov"(X_i, X_j) = "Cov"(X_j, X_i)$.

Variabili aleatorie continue

Definizione

Se $(\Omega, \bar{A}, P)$ è uno spazio di probabilità, una variabile aleatoria (scalare) è una funzione $X: \Omega \to \mathbb{R}$ tale che

$\{\omega \in \Omega: X(\omega) \le t\} \in \bar{A}$ per ogni $t \in \mathbb{R}$

Una variabile aleatoria continua scalare è una variabile aleatoria scalare che può assumere un’infinità non numerabile di valori.

Esempio: la variabile aleatoria $X = "tempo di vita di un animale"$ è una variabile aleatoria continua.

Proprietà

Se $(\Omega, \bar{A}, P)$ è uno spazio di probabilità e $X: \Omega \to \mathbb{R}$ è una variabile aleatoria, allora

$\{\omega \in \Omega: X(\omega) > t \} \in \bar{A}$ per ogni $t \in \mathbb{R}$

$\{\omega \in \Omega: X(\omega) < t\} \in \bar{A}$ per ogni $t \in \mathbb{R}$

$\{\omega \in \Omega: X(\omega) \ge t\} \in \bar{A}$ per ogni $t \in \mathbb{R}$

$\{\omega \in \Omega: X(\omega) = t \} \in \bar{A}$ per ogni $t \in \mathbb{R}$

Per semplicità notazionale, si pone

$\{X \in A\} =_{"def"} \{\omega \in \Omega: X(\omega) \in A\}$

$\{X < t\} =_{"def"} \{\omega \in \Omega: X(\omega) < t\}$

Funzione di distribuzione di probabilità

Se $X$ è una variabile aleatoria, si definisce funzione di distribuzione di probabilità

$F_X(x) = P(\{X \le x\})$

Proprietà

$P(a < X \le b) = F_X(b) – F_X(a)$ (supposto $a < b$)

$P(X > a) = 1 – F_X(a)$

$0 \le F_X(x) \le 1$, per ogni $x \in \mathbb{R}$

$F_X(x)$ è una funzione non decrescente

$\lim_{x \to -\infty} F_X(x) = 0$

$\lim_{x \to +\infty} F_X(x) = 1$

$F_X(x_0) = \lim_{x \to x_0^+} F_X(x)$, per ogni $x_0 \in \mathbb{R}$ ($F_x$ è continua da destra)

Esempio: la funzione di Heaviside, definita da

$H(x) = \{(0, \quad "se " x < 0),(1, \quad "se " x \ge 0):}$

è una funzione di distribuzione di probabilità, infatti ne rispetta tutte le proprietà.

Caso in cui $F_X$ è continua

Se $F_X$ è continua in $x$, allora

$P(X = x) = 0$

Se $F_X$ è continua per ogni $x \in \mathbb{R}$, e $a < b$, allora

$P(a < X < b) = P(a \le X < b) = P(a < X \le b) = P(a \le X \le b)$

Funzione di densità di probabilità

Definizione

Una funzione $f: \mathbb{R} \to \mathbb{R}$ si una dice densità di probabilità se soddisfa queste due proprietà

$f(x) \ge 0 \quad \forall x \in \mathbb{R} \qquad \int_{-\infty}^{+\infty} f(x) dx = 1$

Data una variabile aleatoria $X$ con funzione di distribuzione $F_X(x)$, e data una densità $f(x)$, la variabile $X$ ha densità di probabilità $f_X(x) = f(x)$ se e solo se

$F_X(x) = \int_{-\infty}^x f(u) du$ $\quad \forall x \in \mathbb{R}$

Proprietà

– Se $F_X$ è differenziabile con derivata continua, allora

$f_X(x) = \frac{d}{dx} F_X(x)$

– Se $X$ ammette, come densità, una funzione $f_X(x)$, essa non è unica (basta modificarne il valore in un insieme di misura nulla).

– Se $X$ ha densità di probabilità $f_X(x)$, e $a < b$, allora

$P(a \le X \le b) = \int_a^b f_X(x) dx$

Densità di probabilità continue notevoli

Densità di probabilità uniforme

$f_X(x) = \{(\frac{1}{b-a}, \quad "se " x \in [a,b]),(0, \quad "altrimenti"):}$

Densità di probabilità esponenziale ($\lambda \in \mathbb{R}^+$)

$f_X(x) = \{(0, \quad "se " x < 0),(\lambda e^{-\lambda x}, \quad "se " x \ge 0):}$

Densità di probabilità normale (o gaussiana)

$f_X(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x – \mu)^2}{2 \sigma^2}}$

Variabili aleatorie continue vettoriali

Definizione

Una variabile aleatoria vettoriale continua è un vettore di variabili aleatorie scalari continue

$X = (X_1, X_2, \ldots, X_n)$, oppure $X = ((X_1),(X_2),(\vdots),(X_n))$

dove ogni componente $X_i$, $1 \le i \le n$, è una variabile aleatoria scalare continua.

Funzione di distribuzione di probabilità congiunta

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale, e $x = (x_1, x_2, \ldots, x_n) \in \mathbb{R}^n$ è un generico vettore di $\mathbb{R}^n$, allora la funzione di distribuzione congiunta di $X$ è data da

$F_X(x) = P(\{X_1 \le x_1\} \cap \{X_2 \le x_2\} \cap \ldots \cap \{X_n \le x_n\})$

Funzioni di distribuzione marginali

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale, le funzioni di distribuzione delle componenti di $X$ sono dette funzioni di distribuzioni marginali di $X$.

Caso $n=2$

Se $X = (X_1, X_2)$ è una variabile aleatoria con funzione di distribuzione di probabilità $F_X(x) =F_X(x_1, x_2)$, allora le funzioni di distribuzioni marginali valgono

$F_{X_1}(x_1) = \lim_{x_2 \to +\infty} F_X(x_1, x_2)$

$F_{X_2}(x_2) = \lim_{x_1 \to +\infty} F_X(x_1, x_2)$

Funzione di densità di probabilità congiunta

Una funzione $f: \mathbb{R}^n \to \mathbb{R}$ si dice una densità di probabilità se soddisfa queste due proprietà

$f(x) \ge 0 \quad \forall x \in \mathbb{R}^n \qquad \int_{\mathbb{R}^n} f(x) dx = 1$

Data una variabile aleatoria vettoriale $X$ con funzione di distribuzione $F_X(x)$ e una densità di probabilità $f(x)$, si dice che $X$ ha densità di probabilità $f_X(x) = f(x)$ se e solo se

$F_X(x) = \int_A f(x) dx$

dove $A = \{y \in \mathbb{R}^n: y_1 \le x_1, y_2 \le x_2, \ldots, y_n \le x_n\}$, con $x = (x_1, x_2, \ldots, x_n)$ e $y = (y_1, y_2, \ldots, y_n)$.

Proprietà

– Se $F_X(x)$ è differenziabile su $\mathbb{R}^n$ (tranne al più un numero finito di punti), allora

$f_X(x) = f_X(x_1, x_2, \ldots, x_n) = \frac{\partial^n}{\partial x_1 \partial x_2 \ldots \partial x_n} F_X(x)$

cioè la densità di probabilità congiunta è la derivata $n$-esima mista della funzione di distribuzione congiunta.

– Se $X$ ha densità di probabilità $f_X(x)$, la probabilità di eventi $\{X \in B\}$ equivale a

$P(\{X \in B\}) = \int_B f_X(x) dx$, per ogni $B \subseteq \mathbb{R}^n$

Funzioni di densità di probabilità marginali

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale, le densità di probabilità delle variabili aleatorie scalari $X_1, X_2, \ldots, X_n$ si chiamano densità di probabilità marginali di $X$.

Caso $n = 2$

Se $X = (X_1, X_2)$ ha densità di probabilità $f_X(x_1, x_2)$, le densità di probabilità marginali valgono

$f_{X_1}(x_1) = \int_{-\infty}^{+\infty} f_X(x_1, x_2) d x_2$

$f_{X_2}(x_2) = \int_{-\infty}^{+\infty} f_X(x_1, x_2) d x_1$

Indipendenza e densità condizionali

Definizione

Si dice che $n$ variabili aleatorie $X_1, X_2, \ldots, X_n$ sono indipendenti se e solo se per ogni scelta di $a_1 < b_1, a_2 < b_2, \ldots, a_n < b_n$ risulta

$P(\{a_1 \le X_1 \le b_1\} \cap \{a_2 \le X_2 \le b_2\} \cap \ldots \cap \{a_n \le X_n \le b_n\}) =$

$= P(\{a_1 \le X_1 \le b_1\}) \cdot P(\{a_2 \le X_2 \le b_2\}) \cdot \ldots \cdot P(\{a_n \le X_n \le b_n\})$

Proprietà

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale, le cui componenti sono variabili aleatorie indipendenti, allora la densità congiunta di $X$ è data dal prodotto delle marginali

$f_X(x_1, x_2, \ldots, x_n) = f_{X_1}(x_1) \cdot f_{X_2}(x_2) \cdot \ldots \cdot f_{X_n}(x_n)$

Vale anche il viceversa, cioè se la densità congiunta è data dal prodotto delle marginali, allora le variabili aleatorie $X_1, X_2, \ldots, X_n$ sono indipendenti.

Densità condizionali

Se $X$ e $Y$ sono due variabili aleatorie con densità di probabilità congiunta $f_{X,Y}(x,y)$ e marginali $f_X(x)$ e $f_Y(y)$, si definisce densità di probabilità condizionale di $X$ dato $Y = y$

$f_{X | Y} (x | y) = \{(\frac{f_{X,Y}(x,y)}{f_Y(y)}, \quad "se " f_Y(y) \ne 0),(0, \quad "se " f_Y(y) = 0):}$

Notare che mentre $x$ è una variabile $y$ è fissato.

Caso particolare: indipendenza

Se $X$ e $Y$ sono variabili aleatorie indipendenti, allora le densità condizionali equivalgono alle densità marginali

$f_{X | Y}(x | y) = \frac{f_{X,Y}(x,y)}{f_Y(y)} = \frac{f_X(x) f_Y(y)}{f_Y(y)} = f_X(x)$

$f_{X | Y}(x | y) = \frac{f_{X,Y}(x,y)}{f_X(x)} = \frac{f_X(x) f_Y(y)}{f_X(x)} = f_Y(y)$

Valore atteso, varianza, covarianza (caso continuo)

Valore atteso

Definizione

Si dice che una variabile aleatoria continua $X$ ha speranza matematica finita se e solo se

$\int_{-\infty}^{+\infty} |x| f_X(x) dx < +\infty$ ($f_X$ è la densità di probabilità di $X$)

e in tal caso si chiama valore atteso di $X$ la quantità

$E[X] = \int_{-\infty}^{+\infty} x f_X(x) dx$

Caso vettoriale

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale, il suo valore atteso è il vettore dei valori attesi delle componenti, cioè

$E[X] = (E[X_1], E[X_2], \ldots, E[X_n])$

Proprietà del valore atteso

– Linearità

$E[X + Y] = E[X] + E[Y]$

$E[\alpha X] = \alpha E[X]$, per ogni $\alpha \in \mathbb{R}$

– Valore atteso di una funzione di variabili aleatorie

Se $X = (X_1, X_2, \ldots, X_n)$ è una variabile aleatoria vettoriale con densità congiunta $f_X(x)$ e se $\phi$ è una funzione $\phi: \mathbb{R}^n \to \mathbb{R}$, la variabile aleatoria $\phi(X)$ ha speranza matematica finita se e solo se

$\int_{\mathbb{R}^n} |\phi(x)| f_X(x) dx < +\infty$

e in tal caso il valore atteso di $\phi(X)$ vale

$E[\phi(X)] = \int_{\mathbb{R}^n} \phi(x) f_X(x) dx$

– Valore atteso di un prodotto: se $X$ e $Y$ sono variabili aleatorie indipendenti, allora

$E[X Y] = E[X] E[Y]$

Varianza

Se $X$ è una variabile aleatoria scalare, si definisce varianza di $X$ la quantità

$"Var"(X) = \sigma_X^2 = E[(X – E[X])^2]$

Se $X$ è una variabile aleatoria continua con densità di probabilità $f_X(x)$, allora

$"Var"(X) = \int_{-\infty}^{+\infty} (x – E[X])^2 f_X(x) dx$

La quantità $\sigma_X = \sqrt{"Var"(X)}$ si chiama deviazione standard.

Disuguaglianza di Chebyshev

Fissato $\eta \in \mathbb{R}^+$, risulta

$P(\{|X – E[X]| > \eta\}) \le \frac{"Var"(X)}{\eta^2}$

Proprietà della varianza

$"Var"(X) = E[X^2] – (E[X])^2$

$"Var"(\alpha X) = \alpha^2 "Var"(X)$, per ogni $\alpha \in \mathbb{R}$

$"Var"(\alpha + X) = "Var"(X)$, per ogni $\alpha \in \mathbb{R}$

Covarianza

Date due variabili aleatorie scalari $X$ e $Y$, si definisce covarianza, fra $X$ e $Y$, la quantità

$"Cov"(X, Y) = E[(X – E[X]) \cdot (Y – E[Y])]$

Se $X$ e $Y$ sono variabili aleatorie continue con densità di probabilità congiunta pari a $f_{X,Y}(x,y)$, allora

$"Cov"(X, Y) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x – E[X]) (y – E[Y]) f_{X,Y}(x,y) dx dy$

Proprietà

$"Cov"(X, Y) = E[X Y] – E[X] E[Y]$

$"Var"(X + Y) = "Var"(X) + 2 "Cov"(X, Y) + "Var"(Y)$

$"Cov"(X, Y) = "Cov"(Y, X)$

Coefficiente di correlazione

Date due variabili aleatorie scalari $X$ e $Y$, si definisce coefficiente di correlazione la quantità

$\rho_{X, Y} = \frac{"Cov"(X, Y)}{\sqrt{"Var"(X)} \cdot \sqrt{"Var"(Y)}}$

Due variabili aleatorie si dicono scorrelate se e solo se $\rho_{X, Y} = 0$, cioè se e solo se $"Cov"(X, Y) = 0$, o equivalentemente $E[X Y] = E[X] E[Y]$

Nota: due variabili aleatorie indipendenti sono anche scorrelate, non è vero, in generale, il viceversa.

Matrice di covarianza

Se $X = ((X_1),(X_2),(\vdots),(X_n))$ è una variabile aleatoria vettoriale, si definisce matrice di covarianza di $X$

$\Sigma_X = E[(X – E[X]) \cdot (X – E[X])^T]$ (i vettori sono intesi come colonne)

La matrice di covarianza di $X$ equivale a

Si nota che l’elemento di $\Sigma_X$ di posto $ij$ vale

$\Sigma_{X_{ij}} = \{("Var"(X_i), \quad "se " i = j),("Cov"(X_i, X_j), \quad "se " i \ne j):}$

Proprietà

La matrice di covarianza è simmetrica

$\Sigma_X = \Sigma_X^T$

dato che $"Cov"(X_i, X_j) = "Cov"(X_j, X_i)$.

Valore atteso condizionale

Date due variabili aleatorie continue $X$ e $Y$, il valore atteso condizionale di $X$ dato $Y = y$ vale

$E_{X | Y}[X | y] = \int_{-\infty}^{+\infty} x f_{X | y}(x | y) dx$

Densità normale multivariata

Definizione

Data una variabile aleatoria vettoriale continua $X = (X_1, X_2, \ldots, X_n)$, le variabili aleatorie $X_1, X_2, \ldots, X_n$ si dicono congiuntamente gaussiane se e solo se esistono un vettore $\mu \in \mathbb{R}^n$ e una matrice definita positiva $\Sigma \in \mathbb{R}^{n \times n}$ tali che la densità di probabilità congiunta di $X$ possa essere scritta come

$f_X(x) = \frac{1}{\sqrt{(2 \pi)^n \det(\Sigma)}} e^{-\frac{1}{2} (x – \mu)^T \Sigma^{-1} (x – \mu)}$

Notare che i vettori sono intesi come colonne, quindi $(x – \mu)^T$ è un vettore riga mentre $(x – \mu)$ è un vettore colonna.

Proprietà

Se $X_1, X_2, \ldots, X_n$ sono variabili aleatorie congiuntamente gaussiane, allora $\mu$ è il valore atteso di $X$ mentre $\Sigma$ è la matrice di covarianza di $X$.

Se $X_1, X_2, \ldots, X_n$ sono congiuntamente gaussiane e scorrelate, allora sono anche indipendenti.

Se $X_1, X_2, \ldots, X_n$ sono congiuntamente gaussiane e indipendenti, allora la matrice di covarianza è una matrice diagonale.

Se $X = (X_1, X_2, \ldots, X_n)$ è un vettore di variabili aleatorie congiuntamente gaussiane, comunque si scelgano $A \in \mathbb{R}^{m \times n}$ e $b \in \mathbb{R}^m$, la variabile aleatoria data da

$Y = A X + b$

è un vettore di variabili aleatorie congiuntamente gaussiane, con

$E[Y] = A E[X] + b$

$\Sigma_Y = A \Sigma_X A^T$ ($\Sigma_Y$ e $\Sigma_X$ sono le matrici di covarianza di $Y$ e $X$)

Se $X_1, X_2, \ldots, X_n$ sono variabili aleatorie congiuntamente gaussiane, allora ogni variabile $X_i$, $1 \le i \le n$, è una variabile aleatoria gaussiana.