 Il Premio Galileo per la divulgazione scientifica 2010 viene assegnato a un’opera di diffusione scientifica, in lingua italiana, pubblicata dal 1 gennaio 2008 al 31 dicembre 2009, secondo una formula che si ispira a quella già ampiamente sperimentata del Premio Campiello. Una Giuria Scientifica, quest’anno presieduta dal Prof. Paolo Rossi e composta da scienziati, ricercatori, giornalisti e scrittori, seleziona una cinquina di opere che saranno sottoposte al giudizio di una Giuria Popolare composta da una classe di studenti per ciascuna Provincia italiana, scelta fra le quarte classi delle scuole superiori.
Il Premio Galileo per la divulgazione scientifica 2010 viene assegnato a un’opera di diffusione scientifica, in lingua italiana, pubblicata dal 1 gennaio 2008 al 31 dicembre 2009, secondo una formula che si ispira a quella già ampiamente sperimentata del Premio Campiello. Una Giuria Scientifica, quest’anno presieduta dal Prof. Paolo Rossi e composta da scienziati, ricercatori, giornalisti e scrittori, seleziona una cinquina di opere che saranno sottoposte al giudizio di una Giuria Popolare composta da una classe di studenti per ciascuna Provincia italiana, scelta fra le quarte classi delle scuole superiori.
PREMIO LETTERARIO GALILEO PER LA DIVULGAZIONE SCIENTIFICA – IV EDIZIONE – PADOVA 2010
Paolo Rossi presiede la Giuria scientifica dell’edizione 2010 del premio.
Venerdì 22 gennaio selezione della cinquina finalista in seduta pubblica.
Mercoledì 5 maggio proclamazione del vincitore. 
Quella del 2010 sarà la quarta edizione del Premio letterario Galileo per la divulgazione scientifica che di anno in anno tende sempre più a radicarsi nel panorama culturale italiano, nell’interesse delle case editrici, nell’attenzione dei lettori, soprattutto giovani, nella considerazione della cittadinanza.
Un appuntamento sempre più atteso, quindi, quello promosso dal Comune di Padova e che gode del sostegno della Regione del Veneto e della Provincia di Padova e della collaborazione dell’Università degli Studi di Padova, di ANCI, UPI e di Turismo Padova Terme Euganee e dei patrocini del Ministero per i Beni e le Attività Culturali, del Ministero della Pubblica Istruzione, della Fondazione Il Campiello e dell’Accademia Galileiana di Scienze Lettere ed Arti di Padova.
Un Premio che, per il Sindaco Flavio Zanonato, “l’Amministrazione della città di Padova promuove da anni con l’intento di favorire nei giovani l’interesse per le scienze e il pensiero razionale, presupposto per essere cittadini del mondo”.
Il Premio Galileo per la divulgazione scientifica 2010 viene assegnato a un’opera di diffusione scientifica, in lingua italiana, pubblicata dal 1 gennaio 2008 al 31 dicembre 2009, secondo una formula che si ispira a quella già ampiamente sperimentata del Premio Campiello. Una Giuria Scientifica, quest’anno presieduta dal Prof. Paolo Rossi e composta da scienziati, ricercatori, giornalisti e scrittori, seleziona una cinquina di opere che saranno sottoposte al giudizio di una Giuria Popolare composta da una classe di studenti per ciascuna Provincia italiana, scelta fra le quarte classi delle scuole superiori.
Sono due, quindi, i momenti clou previsti dal Premio. La riunione della Giuria scientifica, costituita da sedici componenti, che si terrà a Padova venerdì 22 gennaio per la selezione della cinquina, scelta tra circa 70 opere, e la proclamazione del vincitore, risultante dalla votazione della Giuria Popolare degli studenti, che si terrà mercoledì 5 maggio 2010 nel Salone del Palazzo della Ragione alla presenza di una delegazione di 110 classi rappresentanti di tutte le province italiane che hanno partecipato alle votazioni.
Il Presidente della Giuria 2010 Paolo Rossi, professore emerito di Storia della Filosofia dell’Università di Firenze, accademico dei Lincei, uno dei più importanti storici della scienza italiani e recente premio Balzan 2009 per la Storia della scienza, succede nell’incarico a Umberto Veronesi, Carlo Rubbia e Margherita Hack.
Rossi vede dei segni positivi per la divulgazione scientifica nel panorama culturale italiano. “Da cinque sei anni a questa parte – afferma – è apparso un certo tipo di libri di divulgazione scientifica di buon livello e si è moltiplicato. Si tratta di un fenomeno relativamente nuovo che dipende dal fatto che si è diffusa presso gli scienziati la consapevolezza che è bene allargare le basi della cultura scientifica e non limitarsi alla ricerca di frontiera. E’ necessario creare un sottofondo culturale per cui il Paese avverta come una cosa importante la cultura scientifica e soprattutto la identifichi come cultura.”
Dal punto di vista della domanda di cultura scientifica per Paolo Rossi la situazione italiana offre elementi di giudizio difformi. “Ci sono dei fenomeni che rattristano e ci sono dei fenomeni consolanti. Tra quelli consolanti c’è il premio Galileo di Padova perché alla fine ci mette in contatto con un migliaio di studenti fortemente interessati al tema, pieni di curiosità, capaci di discutere, capaci di porre domande. Poi ci sono altri fenomeni meno consolanti che sono l’accontentarsi di una divulgazione facile ritenendo che sostituisca il sapere scientifico. Il cambiamento, tuttavia, è abbastanza rilevante ed è positivo.”
Sul Premio Galileo Paolo Rossi ci tiene a un ricordo. “Luigi Luca Cavalli Sforza – vincitore della prima edizione – riuscì a dare agli studenti l’idea che una vita dedicata alla ricerca scientifica è una vita piena e non sprecata. Ne seguì un applauso che per ciascuno di noi fu una ragione di conforto.”
Andrea Colasio, Assessore alla Cultura del Comune di Padova, vede l’imponente lavoro ancora da fare. “In Italia – afferma – la cultura scientifica è molto deficitaria. Ce lo ricorda il rapporto OCS-Pisa che colloca il nostro Paese al 33° posto – su 47 paesi analizzati – per cultura scientifica e al 38° posto per cultura matematica. Si tratta di un portato storico che per buona parte dipende dall’impostazione crociana della nostra formazione che, a differenza di quanto accade nei paesi anglosassoni, privilegia il sapere umanistico a quello scientifico. Questo fatto si risolve poi in meno ricercatori e, in generale, in minor sapere. Padova, da sempre Città della scienza, anche grazie alla sua Università, vuole dare un contributo a invertire questo orientamento. Il Premio Galileo, coerente alla tradizione della città, si inserisce in questa criticità e, con intelligenza e il coinvolgimento di molti giovani studenti, fornisce un contributo importante per la crescita della cultura scientifica”
Il Campiello delle scienze è nato proprio per stimolare nei ragazzi il desiderio di studiare e capire regole e contenuti del sapere scientifico – dalla fisica all’evoluzione, dalle teorie sulla meccanica celeste ai misteri del sistema solare – per provare la forza e il fascino del sapere razionale. Anche quest’anno conduttore della giornata finale sarà il simpatico Patrizio Roversi. Un compito importante e delicato visto l’entusiasmo e la partecipazione che i ragazzi dimostrano nel momento dello scrutinio e poi nell’ascolto degli autori e soprattutto nella capacità e competenza che dimostrano nel porre domande. Segno di una partecipazione autentica, di una lettura intelligente e critica delle opere in concorso. Una partecipazione cresciuta di edizione in edizione e che coinvolge oggi pressoché la totalità delle Province italiane che dimostra come il Premio Galileo e la Città di Padova hanno saputo cogliere una domanda presente e inespressa di partecipazione al sapere dando un contributo alla crescita del pensiero razionale e un servizio e uno stimolo alle giovani generazioni.
I precedenti. Vincitore della prima edizione del Premio Letterario Galileo per la divulgazione scientifica – 2007 – è stato il libro Perché la Scienza? di Luigi Luca e Francesco Cavalli Sforza (Mondadori 2007); nel 2008 ha vinto Se l’uomo avesse le ali di Andrea Frova (ed. RCS libri – BUR 2008). Vincitore della terza edizione 2009, che ha visto la partecipazione di 107 classi del IV anno superiore, provenienti da tutte le province italiane, è stato Energia per l’astronave terra di Nicola Armaroli e Vincenzo Balzani (ed. Zanichelli).
Il 22 gennaio conosceremo la cinquina che si contenderà la vittoria della quarta edizione.

Il Premio Galileo è realizzato con il contributo di: Fondazione Antonveneta, Consorzio Venezia Nuova, Morellato – Gioielli da vivere, Telecom Italia, APS Advertising, Coveco, Società delle Autostrade Venezia e Padova, C.C.I.A.A. Padova, Noleggiami.eu, Consorzio Giotto. Media sponsor: il mattino di Padova, la tribuna di Treviso, la Nuova di Venezia e Mestre, Focus.
Ufficio stampa Studio Lavia – pd 049/8364188 – 348/2628177 (Francesco Nosella) [email protected] – [email protected] www.studiolavia.it
 Nel libro Anche tu matematico di Roberto Vacca, viene illustrato un metodo semplice ed efficace per risolvere manualmente le radici quadrate basato sulla formula che permette di calcolare il quadrato di un binomio. Non è difficile rendersi conto che la procedura illustrata sopra per il calcolo delle radici quadrate si può estendere anche al calcolo delle radici cubiche.
Nel libro Anche tu matematico di Roberto Vacca, viene illustrato un metodo semplice ed efficace per risolvere manualmente le radici quadrate basato sulla formula che permette di calcolare il quadrato di un binomio. Non è difficile rendersi conto che la procedura illustrata sopra per il calcolo delle radici quadrate si può estendere anche al calcolo delle radici cubiche. 
 Sei o cara e amata geometria… contanto le lettere di ogni parola si ottengono le prime cifre di pi greco. Maria Intagliata ha scritto una poesia con diverse centinaia di cife di pi greco.
Sei o cara e amata geometria… contanto le lettere di ogni parola si ottengono le prime cifre di pi greco. Maria Intagliata ha scritto una poesia con diverse centinaia di cife di pi greco.  Il 3° trofeo di scacchi è giunto alla fase conclusiva. I 12 finalisti Firkle, Sergio61, Andreatreno, Ricran, Patrizio20, Cldlomb, Cpeg52, Tusaichi, Paololuigi, Amandy, Pisolo disputano la finale in modalità sincrona, le partite avranno durata massima di 15 minuti per giocatore. Le partite si possono svolgere in qualsiasi ordine e in tempi da concordare tra i giocatori, purché si concludano entro la mezzanotte del 16 dicembre. Tutte le partite della finale si dovranno disputare entro il 21 dicembre, in modo che per il 22 dicembre potremo proclamare i vincitori.. John_doe2266.
Il 3° trofeo di scacchi è giunto alla fase conclusiva. I 12 finalisti Firkle, Sergio61, Andreatreno, Ricran, Patrizio20, Cldlomb, Cpeg52, Tusaichi, Paololuigi, Amandy, Pisolo disputano la finale in modalità sincrona, le partite avranno durata massima di 15 minuti per giocatore. Le partite si possono svolgere in qualsiasi ordine e in tempi da concordare tra i giocatori, purché si concludano entro la mezzanotte del 16 dicembre. Tutte le partite della finale si dovranno disputare entro il 21 dicembre, in modo che per il 22 dicembre potremo proclamare i vincitori.. John_doe2266. 
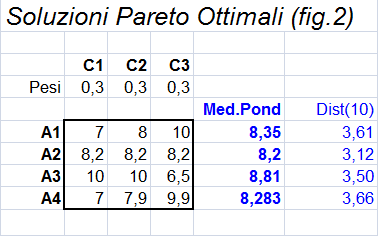
 Per Pareto le scienze economiche e sociali sono caratterizzate dalla forte interdipendenze di tutte le variabili, cosa che rende difficile le attività di previsione e di controllo. Questa situazione obbliga a ricorrere alla "logica matematica che sola può tener conto con ogni ampiezza della interdipendenza". Pareto si è effettivamente servito della matematica in economia e ne ha consigliato l’uso in sociologia, pur senza nutrire eccessive illusioni sulla portata pratica di tale consiglio. Per seguirlo "sarebbe necessario potere assegnare a ciascuna delle cose interdipendenti un indice, è poscia usare della logica matematica, determinando questi indici con un sistema di equazioni".
Per Pareto le scienze economiche e sociali sono caratterizzate dalla forte interdipendenze di tutte le variabili, cosa che rende difficile le attività di previsione e di controllo. Questa situazione obbliga a ricorrere alla "logica matematica che sola può tener conto con ogni ampiezza della interdipendenza". Pareto si è effettivamente servito della matematica in economia e ne ha consigliato l’uso in sociologia, pur senza nutrire eccessive illusioni sulla portata pratica di tale consiglio. Per seguirlo "sarebbe necessario potere assegnare a ciascuna delle cose interdipendenti un indice, è poscia usare della logica matematica, determinando questi indici con un sistema di equazioni". 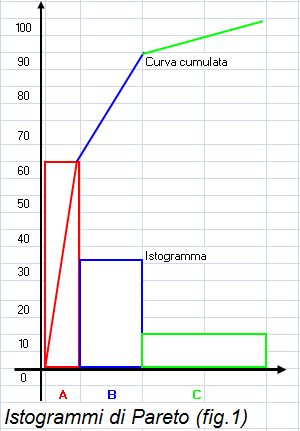
 Festival dello spazio 2010: la convention italiana di Astronomia, Astrofisica, Astronautica… e dintorni. Seconda edizione “Premio Nazionale Divulghiamo la Scienza – Galileo Galilei” riconoscimento per il divulgatore scientifico dell’anno, consegnato allo scienziato ed astronauta italiano Umberto Guidoni. Le due iniziative a Bari domenica 11 aprile 2010, all’interno dello Sheraton Nicolaus Hotel di Bari.
Festival dello spazio 2010: la convention italiana di Astronomia, Astrofisica, Astronautica… e dintorni. Seconda edizione “Premio Nazionale Divulghiamo la Scienza – Galileo Galilei” riconoscimento per il divulgatore scientifico dell’anno, consegnato allo scienziato ed astronauta italiano Umberto Guidoni. Le due iniziative a Bari domenica 11 aprile 2010, all’interno dello Sheraton Nicolaus Hotel di Bari.  Partendo dalle sottostanti formule (A) e (B), dopo vari passaggi che sembrano del tutto regolari, abbiamo ottenuto risultati completamente diversi, (formule (3) e (7)). Abbiamo, però, riscontrato che partendo dalla formula (8) abbiamo ottenuto lo stesso risultato di quello ottenuto partendo dalla formula (B). Appare quindi chiaro che il risultato ottenuto partendo dalla formula (A), formula (3), è quello non attendibile. Poiché il procedimento seguito per ottenere la formula (3) sembra del tutto regolare, chiediamo: dove è l’errore? Le restanti parti rappresentano alcune considerazioni.
Partendo dalle sottostanti formule (A) e (B), dopo vari passaggi che sembrano del tutto regolari, abbiamo ottenuto risultati completamente diversi, (formule (3) e (7)). Abbiamo, però, riscontrato che partendo dalla formula (8) abbiamo ottenuto lo stesso risultato di quello ottenuto partendo dalla formula (B). Appare quindi chiaro che il risultato ottenuto partendo dalla formula (A), formula (3), è quello non attendibile. Poiché il procedimento seguito per ottenere la formula (3) sembra del tutto regolare, chiediamo: dove è l’errore? Le restanti parti rappresentano alcune considerazioni. 121. G. De Cecco, Rompere bene le figure – 122. G. Pesare, Teoria dei giochi e scelte formative – 123. A. Zucco, Poligoni, poliedri e politopi regolari – 124. A. Bonet, Talete il padre dell’astronomia razionale – 125. P. Romano, Simulazioni del decadimento radioattivo con la TI Voyage 200 – 126. A. Urso, Proprietà dell’equazione dei Dieterici – 127. G. Barbella, L’Ovoide a cipolla – 128. S. Lega, Un sistema fuzzy per la modellizzazione delle associazioni biologiche – 129. Recensione: R. J. Aumann, I giochi dell’economia e l’economia dei giochi.
121. G. De Cecco, Rompere bene le figure – 122. G. Pesare, Teoria dei giochi e scelte formative – 123. A. Zucco, Poligoni, poliedri e politopi regolari – 124. A. Bonet, Talete il padre dell’astronomia razionale – 125. P. Romano, Simulazioni del decadimento radioattivo con la TI Voyage 200 – 126. A. Urso, Proprietà dell’equazione dei Dieterici – 127. G. Barbella, L’Ovoide a cipolla – 128. S. Lega, Un sistema fuzzy per la modellizzazione delle associazioni biologiche – 129. Recensione: R. J. Aumann, I giochi dell’economia e l’economia dei giochi.  Robert John Aumann è un matematico israeliano, nel 2005 ha vinto con Thomas Schelling il premio Nobel per l’economia per "avere accresciuto la nostra comprensione del confitto e della cooperazione attraverso l’analisi della Teoria dei Giochi". Secondo i saggi di Stoccolma che lo hanno insignito del premio: “Ha migliorato la nostra comprensione del concetto di conflitto e cooperazione attraverso l’analisi della Teoria dei Giochi come approccio per affrontare la grande questione: perché alcuni gruppi di persone o Paesi riescono a promuovere la cooperazione, mentre altri subiscono i conflitti?”
Robert John Aumann è un matematico israeliano, nel 2005 ha vinto con Thomas Schelling il premio Nobel per l’economia per "avere accresciuto la nostra comprensione del confitto e della cooperazione attraverso l’analisi della Teoria dei Giochi". Secondo i saggi di Stoccolma che lo hanno insignito del premio: “Ha migliorato la nostra comprensione del concetto di conflitto e cooperazione attraverso l’analisi della Teoria dei Giochi come approccio per affrontare la grande questione: perché alcuni gruppi di persone o Paesi riescono a promuovere la cooperazione, mentre altri subiscono i conflitti?”  Una sfida di numeri che ti farà pensare… a lungo. Devi riordinare i numeri da 1 a 52 con una sola condizione da rispettare: ogni numero inserito in una colonna non può essere la somma di due altri numeri che stanno nella stessa colonna. A gioco completato i numeri da 1 a 52 del riquadro di destra devono stare tutti nel riquadro di sinistra… il tutto in un file di Excel.
Una sfida di numeri che ti farà pensare… a lungo. Devi riordinare i numeri da 1 a 52 con una sola condizione da rispettare: ogni numero inserito in una colonna non può essere la somma di due altri numeri che stanno nella stessa colonna. A gioco completato i numeri da 1 a 52 del riquadro di destra devono stare tutti nel riquadro di sinistra… il tutto in un file di Excel.  Il servizio scolastico camba, formulando nuove direttive per l’innovazione della didattica: “uso costante del laboratorio nell’insegnamento delle discipline scientifiche”; “metodologie finalizzate a valorizzare il metodo scientifico e il pensiero operativo”; "valorizzare stili di apprendimento induttivi". Questo scritto ha un duplice obiettivo: da un lato vuole attribuire un univoco significato alle parole chiave della norma fondante l’autonomia scolastica, terreno su cui radicherà il nuovo modello di scuola, dall’altro lato fornire un esempio di didattica laboratoriale. In particolare si presentano e si discutono tre questioni.
Il servizio scolastico camba, formulando nuove direttive per l’innovazione della didattica: “uso costante del laboratorio nell’insegnamento delle discipline scientifiche”; “metodologie finalizzate a valorizzare il metodo scientifico e il pensiero operativo”; "valorizzare stili di apprendimento induttivi". Questo scritto ha un duplice obiettivo: da un lato vuole attribuire un univoco significato alle parole chiave della norma fondante l’autonomia scolastica, terreno su cui radicherà il nuovo modello di scuola, dall’altro lato fornire un esempio di didattica laboratoriale. In particolare si presentano e si discutono tre questioni. 
 Il lavoro di questo seminario si basa sull’articolo General Error Locator Polynomials for Binary Ciclic Codes with t<=2 e n<63 di E. Orsini e M. Sala; all’interno della categoria di codici presa in considerazione, si ritrovano alcuni (pochi) casi in cui la rappresentazione del polinomio locatore è implicita. Questi casi, che elenchiamo di seguito, sono stati studiati recentemente da F. Caruso e M. Sala, illustreremo di seguito una parte dei risultati di queste ricerche.
Il lavoro di questo seminario si basa sull’articolo General Error Locator Polynomials for Binary Ciclic Codes with t<=2 e n<63 di E. Orsini e M. Sala; all’interno della categoria di codici presa in considerazione, si ritrovano alcuni (pochi) casi in cui la rappresentazione del polinomio locatore è implicita. Questi casi, che elenchiamo di seguito, sono stati studiati recentemente da F. Caruso e M. Sala, illustreremo di seguito una parte dei risultati di queste ricerche.  Capitolo 1 Elementi di meccanica classica. La teoria della relatività è, senza ombra di dubbio, una delle più grandi rivoluzioni del pensiero umano, ad opera principalmente del fisico tedesco Albert Einstein. La teoria della relatività generale, sublime capolavoro del pensiero umano, costituisce tuttora, ad ormai un secolo dalla sua stesura, la teoria di riferimento della gravitazione che corregge e amplia la vecchia teoria newtoniana e fa da base per gli attuali tentativi di quantizzazione della gravità. Come ogni teoria fisica anche la teoria della relatività è formalizzata in termini matematici; più precisamente la matematica che pone il fondamento della teoria della relatività è il calcolo tensoriale, costruito e studiato da G. Ricci Curbastro e dal suo allievo T. Levi Civita.
Capitolo 1 Elementi di meccanica classica. La teoria della relatività è, senza ombra di dubbio, una delle più grandi rivoluzioni del pensiero umano, ad opera principalmente del fisico tedesco Albert Einstein. La teoria della relatività generale, sublime capolavoro del pensiero umano, costituisce tuttora, ad ormai un secolo dalla sua stesura, la teoria di riferimento della gravitazione che corregge e amplia la vecchia teoria newtoniana e fa da base per gli attuali tentativi di quantizzazione della gravità. Come ogni teoria fisica anche la teoria della relatività è formalizzata in termini matematici; più precisamente la matematica che pone il fondamento della teoria della relatività è il calcolo tensoriale, costruito e studiato da G. Ricci Curbastro e dal suo allievo T. Levi Civita. 
 Un sussidio didattico semplice ed economico per studiare le tabelline con un metodo manipolativo che consente una costante autocorrezione ottenuta rotando i dischi di cui si compone la "Girandola". Non si clicca, non si scrive, non si sta davanti ad uno schermo: si ruota la girandola che fa apparire, man mano, i risultati delle moltiplicazioni richieste.
Un sussidio didattico semplice ed economico per studiare le tabelline con un metodo manipolativo che consente una costante autocorrezione ottenuta rotando i dischi di cui si compone la "Girandola". Non si clicca, non si scrive, non si sta davanti ad uno schermo: si ruota la girandola che fa apparire, man mano, i risultati delle moltiplicazioni richieste. 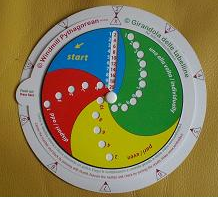




 Le scuole della provincia di Torino si sfidano in vista delle Olimpiadi nazionali a squadre (pomeriggio, rampa del Lingotto) Gara per il pubblico a squadre (pomeriggio, corte della Ristorazione) Dal mattino, conferenze e mostre. TORINO, 12 MARZO 2010 LINGOTTO, VIA NIZZA 230, 1° PIANO
Le scuole della provincia di Torino si sfidano in vista delle Olimpiadi nazionali a squadre (pomeriggio, rampa del Lingotto) Gara per il pubblico a squadre (pomeriggio, corte della Ristorazione) Dal mattino, conferenze e mostre. TORINO, 12 MARZO 2010 LINGOTTO, VIA NIZZA 230, 1° PIANO  In questo lavoro viene presentato un sistema a logica fuzzy, capace di fornire una descrizione formale delle associazioni biologiche tra due specie di popolazioni animali: le lepri e le linci vissute in Canada tra il 1845 ed il 1937. Un sistema fuzzy è un modello matematico che utilizza la teoria dei fuzzy sets e la logica fuzzy e permette di trattare entità non definibili con precisione.
In questo lavoro viene presentato un sistema a logica fuzzy, capace di fornire una descrizione formale delle associazioni biologiche tra due specie di popolazioni animali: le lepri e le linci vissute in Canada tra il 1845 ed il 1937. Un sistema fuzzy è un modello matematico che utilizza la teoria dei fuzzy sets e la logica fuzzy e permette di trattare entità non definibili con precisione.  La prova straordinaria di matematica per il liceo scientifico, anno 2008.
La prova straordinaria di matematica per il liceo scientifico, anno 2008.  Disponi le tessere in modo che su ogni riga e su ogni colonna vi siano tessere distinte per colore o per immagine. Misura la tua intelligenza e sali al primo posto in classifica.
Disponi le tessere in modo che su ogni riga e su ogni colonna vi siano tessere distinte per colore o per immagine. Misura la tua intelligenza e sali al primo posto in classifica.  In un campo a forma di cerchio di raggio 100 metri, una capra è legata da una corda a un paletto, in un punto fisso del recinto. Per impedire alla capra di diventare troppo grassa, l’agricoltore vuole fare in modo che essa possa raggiungere soltanto la metà dell’erba del campo. Quanto deve essere lunga la corda? L’autore ha esplorato gli aspetti geometrici di questo semplice quiz matematico, ottenendo risultati interessanti e una nuova curva a forma di cipolla.
In un campo a forma di cerchio di raggio 100 metri, una capra è legata da una corda a un paletto, in un punto fisso del recinto. Per impedire alla capra di diventare troppo grassa, l’agricoltore vuole fare in modo che essa possa raggiungere soltanto la metà dell’erba del campo. Quanto deve essere lunga la corda? L’autore ha esplorato gli aspetti geometrici di questo semplice quiz matematico, ottenendo risultati interessanti e una nuova curva a forma di cipolla.  Venezia 26 – 28 marzo 2010 Auditorium Santa Margherita, Università Ca’ Foscari. Il convegno, della serie iniziata nel 1997, intende proseguire nell’analisi delle possibili connessioni tra la matematica e altri aspetti del sapere umano. Tra i temi trattati: matematica e arte, matematica e applicazioni, matematica e letteratura, matematica e musica, matematica e misticismo, matematica e architettura.
Venezia 26 – 28 marzo 2010 Auditorium Santa Margherita, Università Ca’ Foscari. Il convegno, della serie iniziata nel 1997, intende proseguire nell’analisi delle possibili connessioni tra la matematica e altri aspetti del sapere umano. Tra i temi trattati: matematica e arte, matematica e applicazioni, matematica e letteratura, matematica e musica, matematica e misticismo, matematica e architettura.  La capacità essenziale dei capi di alto livello è quella direttiva, la capacità essenziale dei quadri intermedi è la professionlaità. Lo scopo della suddivisione del lavoro è produrre di più e meglio col medesimo sforzo. In genere si teme la responsabilità quanto si cerca l’autorità… Un leader capace dovrebbe possedere e infondere in coloro che gli stanno accanto il coraggio di assumersi responsabilità. Quando c’è una carenza evidente di disciplina o quando i rapporti fra superiori e dipendenti lasciano molto a desiderare la causa della disfunzione è da ricercarsi soprattutto nell’inettitudine dei leader.
La capacità essenziale dei capi di alto livello è quella direttiva, la capacità essenziale dei quadri intermedi è la professionlaità. Lo scopo della suddivisione del lavoro è produrre di più e meglio col medesimo sforzo. In genere si teme la responsabilità quanto si cerca l’autorità… Un leader capace dovrebbe possedere e infondere in coloro che gli stanno accanto il coraggio di assumersi responsabilità. Quando c’è una carenza evidente di disciplina o quando i rapporti fra superiori e dipendenti lasciano molto a desiderare la causa della disfunzione è da ricercarsi soprattutto nell’inettitudine dei leader. 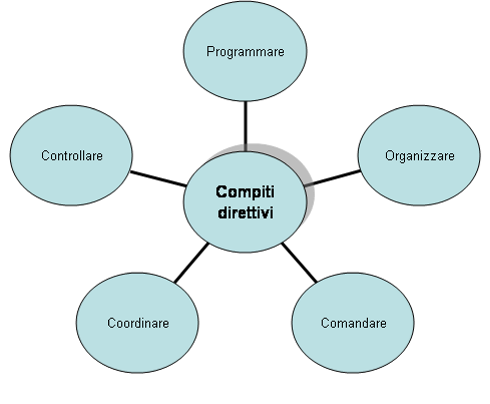
 Il semplice modello della teoria cinetica molecolare, nel quale si schematizzano le molecole come corpuscoli dotati di una certa massa e velocità, è soddisfacente in quanto consente di ricavare la legge di stato dei gas ideali utile nel caso di pressioni molto basse. Sotto condizioni più generali invece i vari gas mostrano deviazioni non trascurabili. Sorge allora spontanea la domanda sulla possibilità di poter comprendere la natura di queste deviazioni usando per un gas un modello più elaborato; è pertanto molto interessante indagare su quali ritocchi siano necessari al modello precedente.
Il semplice modello della teoria cinetica molecolare, nel quale si schematizzano le molecole come corpuscoli dotati di una certa massa e velocità, è soddisfacente in quanto consente di ricavare la legge di stato dei gas ideali utile nel caso di pressioni molto basse. Sotto condizioni più generali invece i vari gas mostrano deviazioni non trascurabili. Sorge allora spontanea la domanda sulla possibilità di poter comprendere la natura di queste deviazioni usando per un gas un modello più elaborato; è pertanto molto interessante indagare su quali ritocchi siano necessari al modello precedente.  La prova svolta di matematica per la maturità 2008, sessione straordinaria, liceo scientifico sperimentale PNI.
La prova svolta di matematica per la maturità 2008, sessione straordinaria, liceo scientifico sperimentale PNI.  L’investimento che meglio difende dall’inflazione non è quotato in Borsa, non si sottoscrive alle Poste né viene offerto dai promotori finanziari. È nominativo, non trasferibile e può durare fino all’età della pensione. Si tratta infatti del tanto discusso Tfr (Trattamento di fine rapporto). Basti dire che il suo potere d’acquisto, al netto delle imposte, si conserva persino con 30 anni d’inflazione al 7%, equivalenti a un aumento complessivo del costo della vita superiore al 650%. Nessun altro investimento è così difensivo, per cui non appare furba la soluzione d’incassare il Tfr alla fine di ogni anno, come accade per esempio a San Marino.
L’investimento che meglio difende dall’inflazione non è quotato in Borsa, non si sottoscrive alle Poste né viene offerto dai promotori finanziari. È nominativo, non trasferibile e può durare fino all’età della pensione. Si tratta infatti del tanto discusso Tfr (Trattamento di fine rapporto). Basti dire che il suo potere d’acquisto, al netto delle imposte, si conserva persino con 30 anni d’inflazione al 7%, equivalenti a un aumento complessivo del costo della vita superiore al 650%. Nessun altro investimento è così difensivo, per cui non appare furba la soluzione d’incassare il Tfr alla fine di ogni anno, come accade per esempio a San Marino.  Abstract. A graphical calculator, as TI Voyage 200, can be used to simulate stochastic processes through its pseudo-casual number generator. In this work, we realize a simulation of nuclear decay, to verify the laws governing this process.
Abstract. A graphical calculator, as TI Voyage 200, can be used to simulate stochastic processes through its pseudo-casual number generator. In this work, we realize a simulation of nuclear decay, to verify the laws governing this process.  L’autore fa una breve introduzione sulle origini dell’astronomia, passa in rassegna le classiche fonti storiche sulla vita e le opere di Talete e sulla cultura dell’antico Egitto, espone un metodo per la misurazione delle altezze delle piramidi che potrebbe essere stato usato dal grande saggio dell’antichità. Immagina anche la realizzazione di un ipotetico distanziometro per misurare dalla costa le distanze delle navi in mare, il quale permette anche di spiegare la scoperta dei teoremi geometrici e la predizione di eventi astronomici che la tradizione attribuisce a Talete.
L’autore fa una breve introduzione sulle origini dell’astronomia, passa in rassegna le classiche fonti storiche sulla vita e le opere di Talete e sulla cultura dell’antico Egitto, espone un metodo per la misurazione delle altezze delle piramidi che potrebbe essere stato usato dal grande saggio dell’antichità. Immagina anche la realizzazione di un ipotetico distanziometro per misurare dalla costa le distanze delle navi in mare, il quale permette anche di spiegare la scoperta dei teoremi geometrici e la predizione di eventi astronomici che la tradizione attribuisce a Talete.  "La verità è l’opinione destinata ad essere accettata all’ultimo da tutti coloro che investigano". "Se una certa sorta di sostanza è sottoposta ad una certa sorta di azione ne conseguirà una certa sorta di risultato conforme all’esperienza sinora acquisita". "Il concetto di tutti i possibili effetti prodotti da un oggetto è il concetto completo di quel oggetto". Charles S. Peirce (1839, 1914), filosofo, logico, matematico.
"La verità è l’opinione destinata ad essere accettata all’ultimo da tutti coloro che investigano". "Se una certa sorta di sostanza è sottoposta ad una certa sorta di azione ne conseguirà una certa sorta di risultato conforme all’esperienza sinora acquisita". "Il concetto di tutti i possibili effetti prodotti da un oggetto è il concetto completo di quel oggetto". Charles S. Peirce (1839, 1914), filosofo, logico, matematico.  Regolamento internazionale del gioco degli scacchi – Glossario scacchistico – Alcune abbreviazioni – Campionato Italiano e femminile) – Campionato Italiano per corrispondenza maschile e femminile – Campionato Italiano di Soluzione ASI – Campioni del Mondo indiscussi – Campionato del Mondo e femminile -Campionato del Mondo per corrispondenza – La Morale degli Scacchi di B. Franklin – Nozioni elementari sul problema in due mosse di G. Mentasti – Anniversari di Scacchisti – Bibliografia essenziale italiana – Indirizzi internet – Filatelia scacchistica – Fotografie di scacchisti e problemisti.
Regolamento internazionale del gioco degli scacchi – Glossario scacchistico – Alcune abbreviazioni – Campionato Italiano e femminile) – Campionato Italiano per corrispondenza maschile e femminile – Campionato Italiano di Soluzione ASI – Campioni del Mondo indiscussi – Campionato del Mondo e femminile -Campionato del Mondo per corrispondenza – La Morale degli Scacchi di B. Franklin – Nozioni elementari sul problema in due mosse di G. Mentasti – Anniversari di Scacchisti – Bibliografia essenziale italiana – Indirizzi internet – Filatelia scacchistica – Fotografie di scacchisti e problemisti. Come ricondurre alla fisica la teoria economica del ’’Dividend Discount Model’’ e trasferire al mercato finanziario le regole della “termodinamica generalizzata” ricorrendo a un totale cambiamento di prospettiva rispetto a quella assunta dalla Reh (Rational expectations hypothesis) i cui limiti, nel prevedere crisi sistemiche, sono emersi anche nell’ultima crisi finanziaria.
Come ricondurre alla fisica la teoria economica del ’’Dividend Discount Model’’ e trasferire al mercato finanziario le regole della “termodinamica generalizzata” ricorrendo a un totale cambiamento di prospettiva rispetto a quella assunta dalla Reh (Rational expectations hypothesis) i cui limiti, nel prevedere crisi sistemiche, sono emersi anche nell’ultima crisi finanziaria.  La verità dà fastidio a chi prospera sull’inganno. Non stupiscono quindi le reazioni a un recente servizio sulla previdenza integrativa, realizzato in maniera magistrale da Piero Riccardi e trasmesso da Rai3 nella puntata di Report del 15 novembre 2009. Venivano fuori infatti le perdite anche per soluzioni gabellate per sicure, la generale assenza di trasparenza e gli endemici conflitti d’interesse, tipici del settore.
La verità dà fastidio a chi prospera sull’inganno. Non stupiscono quindi le reazioni a un recente servizio sulla previdenza integrativa, realizzato in maniera magistrale da Piero Riccardi e trasmesso da Rai3 nella puntata di Report del 15 novembre 2009. Venivano fuori infatti le perdite anche per soluzioni gabellate per sicure, la generale assenza di trasparenza e gli endemici conflitti d’interesse, tipici del settore.  1° classificato: CPEG52 (Antonio Motta di Usmate Velate, MB) vince la coppa e la PS3.
1° classificato: CPEG52 (Antonio Motta di Usmate Velate, MB) vince la coppa e la PS3.



 Vai ai quesiti >>>
Vai ai quesiti >>> “Tutte le più alte prove della scienza e della virtù si svolgono negli accordi e disaccordi degli uomini posti tra loro in intima relazione. Rimase ad indagarsi per quali altri modi, oltre al linguaggio, le menti associate nelle famiglie, nelle classi, nei popoli, nel genere umano, potessero collaborare alla comune intelligenza, ovvero contrariarla. Ciò che caratterizza una idea nuova è ch’ella nasce dal conflitto di più menti …”
“Tutte le più alte prove della scienza e della virtù si svolgono negli accordi e disaccordi degli uomini posti tra loro in intima relazione. Rimase ad indagarsi per quali altri modi, oltre al linguaggio, le menti associate nelle famiglie, nelle classi, nei popoli, nel genere umano, potessero collaborare alla comune intelligenza, ovvero contrariarla. Ciò che caratterizza una idea nuova è ch’ella nasce dal conflitto di più menti …” 
 Se le definizioni di poligono (2 dimensioni) e di poliedro (3 dimensioni) sono ben note, per poter parlare di oggetti in dimensione superiore a 3 (politopi), occorre dare una definizione estendibile a un qualsiasi numero di dimensioni. In questo sintetico articolo vengono discusse definizioni e proprietà dei politopi.
Se le definizioni di poligono (2 dimensioni) e di poliedro (3 dimensioni) sono ben note, per poter parlare di oggetti in dimensione superiore a 3 (politopi), occorre dare una definizione estendibile a un qualsiasi numero di dimensioni. In questo sintetico articolo vengono discusse definizioni e proprietà dei politopi.  Il Premio Galileo per la divulgazione scientifica 2010 viene assegnato a un’opera di diffusione scientifica, in lingua italiana, pubblicata dal 1 gennaio 2008 al 31 dicembre 2009, secondo una formula che si ispira a quella già ampiamente sperimentata del Premio Campiello. Una Giuria Scientifica, quest’anno presieduta dal Prof. Paolo Rossi e composta da scienziati, ricercatori, giornalisti e scrittori, seleziona una cinquina di opere che saranno sottoposte al giudizio di una Giuria Popolare composta da una classe di studenti per ciascuna Provincia italiana, scelta fra le quarte classi delle scuole superiori.
Il Premio Galileo per la divulgazione scientifica 2010 viene assegnato a un’opera di diffusione scientifica, in lingua italiana, pubblicata dal 1 gennaio 2008 al 31 dicembre 2009, secondo una formula che si ispira a quella già ampiamente sperimentata del Premio Campiello. Una Giuria Scientifica, quest’anno presieduta dal Prof. Paolo Rossi e composta da scienziati, ricercatori, giornalisti e scrittori, seleziona una cinquina di opere che saranno sottoposte al giudizio di una Giuria Popolare composta da una classe di studenti per ciascuna Provincia italiana, scelta fra le quarte classi delle scuole superiori. 

 Riprende la scuola, tra una lezione a l’altra il tempo di fare qualche esercizio logico-mentale si trova sempre. Ecco i nuovi Sudoku:
Riprende la scuola, tra una lezione a l’altra il tempo di fare qualche esercizio logico-mentale si trova sempre. Ecco i nuovi Sudoku:  In quest’articolo si mostra come la teoria dei giochi può spiegare alcuni fenomeni sociali, quali gli effetti non intenzionali dell’agire sociale, in particolare viene presentato un modello proposto da R. Boudon per spiegare l’insuccesso dell’insegnamento superiore corto, introdotto negli anni ’60 nel sistema universitario francese.
In quest’articolo si mostra come la teoria dei giochi può spiegare alcuni fenomeni sociali, quali gli effetti non intenzionali dell’agire sociale, in particolare viene presentato un modello proposto da R. Boudon per spiegare l’insuccesso dell’insegnamento superiore corto, introdotto negli anni ’60 nel sistema universitario francese.  Robert John Aumann è un matematico israeliano, nel 2005 ha vinto con Thomas Schelling il premio Nobel per l’economia per "avere accresciuto la nostra comprensione del confitto e della cooperazione attraverso l’analisi della Teoria dei Giochi". Secondo i saggi di Stoccolma che lo hanno insignito del premio: “Ha migliorato la nostra comprensione del concetto di conflitto e cooperazione attraverso l’analisi della Teoria dei Giochi come approccio per affrontare la grande questione: perché alcuni gruppi di persone o Paesi riescono a promuovere la cooperazione, mentre altri subiscono i conflitti?”
Robert John Aumann è un matematico israeliano, nel 2005 ha vinto con Thomas Schelling il premio Nobel per l’economia per "avere accresciuto la nostra comprensione del confitto e della cooperazione attraverso l’analisi della Teoria dei Giochi". Secondo i saggi di Stoccolma che lo hanno insignito del premio: “Ha migliorato la nostra comprensione del concetto di conflitto e cooperazione attraverso l’analisi della Teoria dei Giochi come approccio per affrontare la grande questione: perché alcuni gruppi di persone o Paesi riescono a promuovere la cooperazione, mentre altri subiscono i conflitti?”  Il 2009 si concluderà in bellezza con una Luna Blu, almeno per chi avrà modo di vederla, date le previsioni meteo. Al contrario del fenomeno della Luna Rossa, in cui effettivamente la nostra Luna appare rossastra, il fenomeno della Luna Blu non è legato ad alcuna variazione cromatica. Il termine Luna Blu, deriva dall’anglosassone Blue Moon, e indica semplicemente la presenza di due lune piene nello stesso mese. E’ un fenomeno abbastanza raro, accade circa una volta ogni due anni e mezzo. Quest’anno tuttavia apparirà anche una macchia nera.
Il 2009 si concluderà in bellezza con una Luna Blu, almeno per chi avrà modo di vederla, date le previsioni meteo. Al contrario del fenomeno della Luna Rossa, in cui effettivamente la nostra Luna appare rossastra, il fenomeno della Luna Blu non è legato ad alcuna variazione cromatica. Il termine Luna Blu, deriva dall’anglosassone Blue Moon, e indica semplicemente la presenza di due lune piene nello stesso mese. E’ un fenomeno abbastanza raro, accade circa una volta ogni due anni e mezzo. Quest’anno tuttavia apparirà anche una macchia nera. 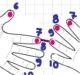 Antichi metodi ormai dimenticati per eseguire le moltiplicazioni con le dita delle mani, una interessante curiosità per gli uomini del 2010.
Antichi metodi ormai dimenticati per eseguire le moltiplicazioni con le dita delle mani, una interessante curiosità per gli uomini del 2010.  Queste ricerche… esibiscono il linguaggio non come una mera collezione di segni, ma come un sistema d’espressioni, i cui elementi sono soggetti alle leggi del pensiero che esse rappresentano. Che queste leggi siano matematicamente rigorose… è una conclusione che io non esito a sottoporre al controllo più severo.
Queste ricerche… esibiscono il linguaggio non come una mera collezione di segni, ma come un sistema d’espressioni, i cui elementi sono soggetti alle leggi del pensiero che esse rappresentano. Che queste leggi siano matematicamente rigorose… è una conclusione che io non esito a sottoporre al controllo più severo.