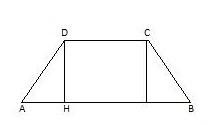
Il pentagono $ABCE$ è formato dal triangolo isoscele $hat{ABD}$ e dai due triangoli equilateri congruenti $hat{BCD}$ e $hat{ADE}$.
Sapendo che la base e l’altezza del triangolo isoscele sono una i $3/2$ dell’altra e la loro somma è $360cm$,
calcola il perimetro e l’area del pentagono.
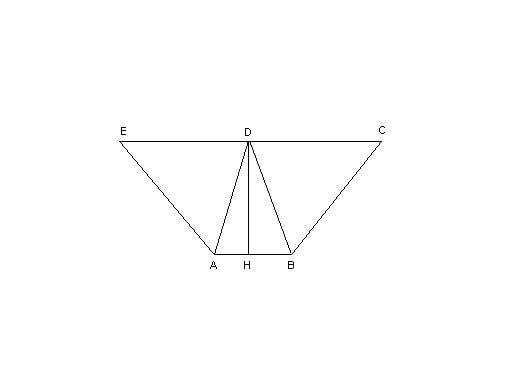
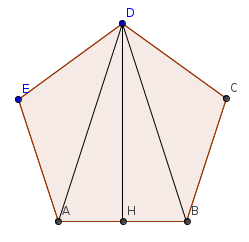
Dati
$bar(AB)=3/2bar(DH)$
$bar(AB)+bar(DH)=360cm$
$A_p$ =area del pentagono
Svolgimento
Il fatto che $bar(AB)=3/2bar(DH)$, significa che dividendo la base in $5$ parti uguali, l’altezza
è individuata da sole $3$ parti, uguali alle precedenti, per cui sommando altezza e base si
ottengono $5$ parti uguali.
Sapendo che la somma di queste parti è $360cm$, per individuare la misura di ciascuna parte si
procede con la seguente operazione
$(360)/5cm=72cm$.
Quindi $bar(AB)=3*72cm=144cm$ e $bar(DH)=2*72cm=216cm$.
Inoltre $bar(AH)=(bar(AB))/2=(144cm)/2=72cm$
Applicando il Teorema di Pitagora, troviamo l’ipotenusa $bar(AD)$ del triangolo rettangolo $hat{AHD}$
$bar(AD)=sqrt((bar(AH))^2+(bar(DH))^2)$=
$sqrt((72cm)^2-(216cm)^2)$=
$sqrt(5184+46656)cm=sqrt(51840)cm=227,68cm$.
Per ipotesi $bar(AD)=bar(DB)=bar(AE)=bar(ED)=bar(DC)=bar(CB)$, pertanto il perimetro del pentagono sarà
$2p=bar(AB)+bar(BC)+bar(DC)+bar(DE)+bar(AE)$=
$(144+(227,68*4))cm=(144+910,72)cm=1054,72cm$
Calcoliamo ora l’area del triangolo isoscele $hat{ABD}$
$A_(ABD)=((bar(AB))(bar(DH)))/2=((216)(144))/2cm^2=15552cm^2$.
Calcoliamo ora l’altezza relativa al triangolo equilatero $hat{BCD}$, mediante il Teorema di Pitagora
$bar(CK)=sqrt((bar(CB))^2-(bar(KB))^2)$
dove $bar(KB)=(bar(DB))/2=(227,68cm)/2=113,84cm$
$sqrt((bar(CB))^2-(bar(KB))^2)$=
$sqrt((227,68cm)^2-(113,84cm)^2)=sqrt(64797.72)cm=254.55cm$
Calcoliamo ora l’area del triangolo equilatero $hat{BCD}$, che naturalmente risulterà
essere uguale a quella del triangolo equilatero $hat{ADE}$
$A_(BCD)=((bar(DB))(bar(CK)))/2$=
$((227,68)(254,55))/2cm^2=28978,42cm^2$
Pertanto l’area del pentagono sarà data dalla somma delle aree dei tre triangoli che lo compongono
$A_p=A_(ABD)+A_(BCD)+A_(ADE)$=
$(28978,42+28978,42+15552)cm^2=73508.85cm^2$.

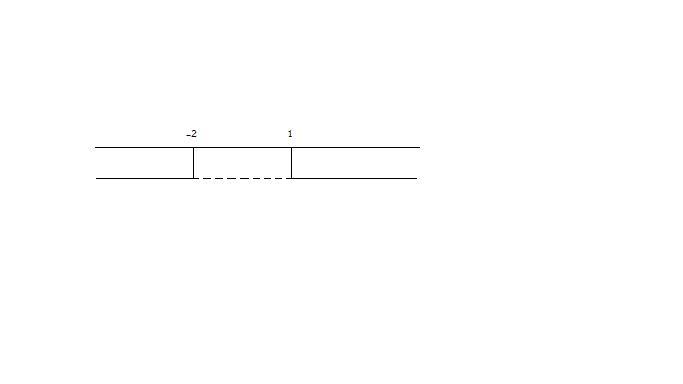
 Ipotesi
Ipotesi Dati
Dati Dati
Dati Dati
Dati

 Dati:
Dati: