Pitagora,filosofo e matematico greco (Samo, 585 – 565 a.C. Metaponto, 495 – 470).
Costretto a lasciare la sua patria, forse a causa della tirannia di Policrate, si recò nella Magna Grecia e a Crotone dove, verso il 530, fondò la sua scuola.
L’attività politica che la comunità pitagorica svolgeva a favore del regime aristocratico suscitò una violenta reazione popolare; la scuola fu incendiata e i pitagorici furono massacrati. Non è certo se anche Pitagora sia morto in quella circostanza o se, riuscito a fuggire, si sia rifugiato a Metaponto morendovi poco dopo.
Pitagora non è solo uno dei più grandi filosofi antichi, ma è pure il fondatore di una scuola che ha avuto una storia di più di dieci secoli: la scuola pitagorica. Tuttavia, è proprio tale circostanza che impedisce di sapere con certezza quali dottrine spettino propriamente a lui e quali ai suoi seguaci: il rigido principio di autorità, vigente nella scuola, espresso dalla formula “ipse dixit”, induceva a porre sotto il prestigioso nome del fondatore anche le dottrine posteriori. A ciò si aggiunga che Pitagora diventò ben presto un personaggio leggendario: figlio di Apollo o di Ermes, nelle sue precedenti incarnazioni (la sua anima sarebbe stata nel corpo di Euforbo al tempo della guerra di Troia), era capace di profezie e di miracoli, era stato il solo a udire le armonie delle sfere celesti, era sceso nell’Ade, eccetera.
Resta comunque il fatto che autori cronologicamente a lui vicini (Senofane, Pindaro, Erodoto) gli attribuiscono la dottrina della trasformazione delle anime (metempsicosi) e quella della respirazione cosmica, oltre ad una vastissima dottrina in tutti i campi.
La dottrina della "purificazione " delle anime mediante la scienza (soprattutto aritmetica e geometria) e la musica spiega l’attribuzione a Pitagora non solo numerose scoperte in questi campi, ma anche la dottrina fondamentale della scuola, quella per cui l’essenza delle cose sta nei numeri e nei rapporti matematici.
Il Teorema di Pitagora, lo troviamo nella quarantasettesima proposizione del primo libro di Euclide; essa dice che in un qualunque triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
La leggenda vuole che Pitagora decretasse un’ecatombe per ringraziare gli dei della scoperta. In verità, il "fatto" geometrico era conosciuto prima di Pitagora; quanto alla sua dimostrazione razionale e non empirica, si ritiene che sia successiva a Pitagora. Non è quindi molto chiaro fino a che punto il filosofo di Samo fosse legato al teorema che porta il suo nome.
La scuola pitagorica è una delle scuole filosofiche più importanti della Grecia. Fondata da Pitagora ebbe più di dieci secoli di vita, con periodi di grande rigoglio e altri di eclisse. Tra i discepoli più vicini a Pitagora sono ricordati, Cercope, Petrone, Brotino e Ippaso e al suo insegnamento è collegato anche il matematico Alcmeone.
Pitagora aveva posto la sede della sua scuola a Crotone, ma abbiamo notizia di altri sodalizi pitagorici nella Magna Grecia (Archippo e Clinia a Reggio e poi Archita a Taranto). Alcuni pitagorici, poi, dopo la repressione violenta si trasferirono nella Grecia continentale: la scuola pitagorica rifiorì soprattutto a Tebe con Filolao e i suoi discepoli Simmia, Cebete (gli interlocutori di Socrate nel Fedone platonico) e Liside. Altri pitagorici di questo periodo sono Eurito, Ocello Lucano, Timeo di Locri, Ecfanto e Iceta.
Arriviamo così all’età di Platone (che con il pitagorismo ebbe rapporti assai importanti e fecondi), con la quale si fa generalmente terminare la storia del pitagorismo antico. Ma la tradizione della scuola non si spense: personalità come quelle di Diodoro di Aspendo, di Eraclide Lembo e di Ningidio Figulo ne assicurarono la continuità fino alla rigogliosa rinascita del I sec. a. C. (scuola neopitagorica).
La primitiva comunità pitagorica è presentata come un’associazione religiosa, politica e scientifica, alla quale si accedeva dopo prove severe, tra cui spiccava il silenzio imposto ai novizi. Gli aderenti erano tenuti al segreto e divulgare le dottrine della scuola poteva costare la vita, come si narra di Ippaso (al quale la tradizione attribuisce la scoperta del concetto di grandezze incommensurabili), reo di aver comunicato un segreto matematico.
Vigevano nella scuola la comunità dei beni, il celibato e una di serie di prescrizioni, che rappresentavamo un vero e proprio "catechismo " di vita pitagorica (astenersi dalle fave, dalla carne, dalle vesti di lana; non raccogliere quel che è caduto in terra, fare tutte le mattine il programma della giornata e tutte le sere un esame di coscienza, ecc.).
Accanto a tali prescrizioni vi era poi una serie di quesiti, le cui risposte erano chiamate, acusmata (per esempio; "che cosa c’è di più saggio?" "il numero"). La dottrina fondamentale della scuola consisteva nell’affermazione che la sostanza delle cose fosse nei numeri e nei rapporti matematici, onde l’importanza di alcuni numeri: l’1 è l’intelligenza, il 2 è l’opinione, il 4 o il 9 (quadrati del primo pari e del primo dispari) la giustizia, il 5 è il matrimonio (l’unione del primo pari e del primo dispari) e soprattutto importante è il 10, la " mistica decade " su cui i pitagorici giuravano, e in cui per la prima volta sono compresi il " parimpari " cioè l’unità, il primo pari, il primo dispari e il primo quadrato.
L’opposizione di pari e dispari sta alla base delle serie delle altre nove opposizioni fondamentali (illimitato – limite, molteplice – unità, maschio-femmina, ecc.).
Esempio di un altro sviluppo in tale direzione è la teoria delle medie matematiche, le più importanti delle quali sono: la media aritmetica $b = (a + c)/2$, cioè b è tale che $a-b=b-c$; la media geometrica $b = sqrt(a*c)$, cioè b è tale che $a: b = b: a$; la media armonica $b=(2a*c)/(a + c)$ l’inverso della media aritmetica degli inversi di a e c, cioè b è tale che $(a-b):(b-c)= a:c$.
Da questa serie di opposizioni nasce poi quell’armonia che è propria di tutto il cosmo, ma che particolarmente si rivela negli accordi musicali.
Anche l’anima era concepita come armonia che, attraverso una serie di purificazioni, tende alla contemplazione dell’armonia celeste. In conformità a tale concezione dell’armonia i pitagorici costruirono la loro particolare cosmologia: attorno al fuoco centrale ruotano i dieci corpi celesti, all’esterno la regione delle stelle fisse, in mezzo la regione dei cinque pianeti, del Sole e della Luna e, più in basso, la regione sublunare, regno del divenire e dell’imperfezione.
Per completare la serie decadica, i pitagorici introdussero l’"antiterra", posta tra la Terra e il fuoco centrale, con cui spiegavano le eclissi, poiché il Sole e la Luna riflettono come specchi il fuoco centrale.
Un posto importante, infine, spetta ai pitagorici nella storia della retorica antica come la medicina cura il corpo, così la musica e la retorica, curano le anime; e l’arte dei discorsi é essenzialmente " psicagogia", cioè trascinamento e guida dell’anima.
Non è possibile discernere l’originaria filosofia di Pitagora dagli apporti successivi dei pitagorici, nel corso dei secoli (già Aristotele, nel IV secolo, parla sempre e solo del pensiero dei pitagorici, facendo vedere così di non sapere nessuna cosa di preciso sul pensiero del fondatore della setta). Si è pensato altresì che la scuola abbia cominciato a occuparsi di filosofia solo parecchio tempo dopo la morte del suo maestro. Ai giorni nostri però si torna a pensare che la maggior parte delle teorie del pitagorismo discenda da Pitagora stesso. Infatti, Pitagora, insieme ai suoi seguaci, non si occupò solamente dello studio generale della matematica, ma altresì di altre discipline, come l’astronomia.
In quest’ambito, grazie ai suoi studi sui numeri, essi furono in grado di rendere comprensibile il moto dei corpi celesti e la struttura atomica dell’universo: sono stati i primi a introdurre la teoria sulla sfericità della Terra e degli astri in genere. Loro consideravano, infatti, la sfera come la più completa delle forme solide, poiché tutti i suoi punti hanno uguale distanza dal centro, ed era vista come una figura dell’armonia. L’ordine dell’universo era descritto come un’armonia di corpi contenuti da un’unica sfera che si muovono secondo un indicato schema numerico: poiché i pitagorici rappresentavano i corpi celesti reciprocamente separati da intervalli che corrispondevano alle lunghezze armoniche delle corde, essi consideravano che il movimento delle sfere producesse un suono, l’ "armonia delle sfere".
Ebbero pure fantasiose illuminazioni che li fanno anticipatori di Copernico. Il pitagorico Filolao abbandonò per primo l’idea che la Terra fosse il centro fisso del mondo, sostenuta invece da Pitagora, pensando che essa, come gli altri corpi, si muoveva attorno ad un fuoco centrale denominato Hestia, "focolare o altare dell’universo", che sistema e plasma la materia vicina, dando origine al mondo.
Egli ritenne inoltre che intorno al fuoco centrale si muovano, da occidente a oriente, dieci corpi celesti e che il cosmo fosse suddiviso in tre domini concentrici:
• L’Olimpo, dove si trovano le stelle fisse;
• Il Mondo, dove vi è Saturno, Giove, Mercurio, Marte, Venere, il Sole (grande lente che rastrella i raggi del fuoco centrale e li riflette) e la Luna;
• Il Cielo (che per i pitagorici è l’elemento soggetto a concepimento e a corruzione), nel quale risiedono la Terra e l’Antiterra, un decimo corpo che i pitagorici hanno introdotto per acquisire il numero perfetto 10; tale corpo è però impercettibile, dato che è sempre in opposizione alla Terra.
Un altro pitagorico, Ecfanto di Siracusa, è stato il primo ad ammettere la roteazione della Terra attorno al proprio asse, posto nella parte del fuoco centrale e dell’Antiterra.
Con Aristarco di Samo, la teoria pitagorica del movimento della Terra si convertì in una vera e propria teoria eliocentrica, poiché, in cambio del fuoco centrale, egli pose il Sole, precorrendo Copernico. La sua dottrina, nonostante tutto, fu sommersa dalla teoria geocentrica di tipo aristotelico – tolemaico.
Tra le pratiche per la depurazione del corpo e dell’anima i pitagorici prediligevano la musica che li portò a scoprire il rapporto numerico alla base dell’altezza dei suoni che, secondo la leggenda, Pitagora trovò riempiendo con dell’acqua un’anfora che percossa diffondeva una nota, in seguito togliendo una parte ben definita dell’acqua, si otteneva un’altra nota maggiore di un’ottava.
È probabile che proprio da tali esperienze musicali nascesse nei pitagorici l’attenzione per l’aritmetica, vista come una dottrina dei numeri interi che essi ritenevano non un’entità irreale, ma concreta; i numeri erano pensati come grandezze spaziali che hanno una stessa estensione e forma, ed erano rappresentati sul piano geometrico e nello spazio (il numero uno era il punto, il due la linea, il tre lo spazio, il quattro il solido).
Pitagora espresse per di più la rilevante dottrina della tetraktys. L’etimologia del termine indicherebbe "numero triangolare". Infatti, per i Pitagorici la tetraktys consisteva in una disposizione geometrica che esprimeva un numero, o un numero espresso da una posizione geometrica. Essa era rappresentata come un triangolo alla cui base erano quattro punti che diminuivano sino alla punta; l’ammontare di tutti i punti era dieci, il numero perfetto risultante dalla somma dei primi quattro numeri (1+2+3+4=10), che abbinati tra loro definivano le quattro specie di enti geometrici: il punto, la linea, la superficie, il solido. La tetraktys aveva un carattere religioso e i pitagorici prestavano giuramento su di essa. Era per di più l’esempio teorico della loro analisi dell’universo, vale a dire un mondo non governato dal caos delle forze tetre, ma da numeri, armonia, rapporti numerici.
Tale matematica pitagorica che fu chiamata un’"aritmogeometria" sostenne la concezione del numero visto come archè, vale a dire principio originario di qualunque cosa. Sino a quel momento, i filosofi naturalisti avevano fatto collimare la sostanza conferendogli delle qualità. Queste però, derivando dalla sensibilità, erano variabili e mettevano in discussione la peculiarità principale della sostanza: la sua invariabilità. I pitagorici ritenevano di superare tale difficoltà ponendo in evidenza che se è vero che i principi originari mutano sul piano qualitativo, essi, però serbano la quantità che è calcolabile e di conseguenza formulabili in numeri, vero ultimo fondamento del mondo reale.
Diceva Filolao: «Tutte le cose che si conoscono hanno numero; senza questo, nulla sarebbe possibile pensare, né conoscere». Pitagora cercò di scoprire i legami tra i suoni e l’ordine celato della natura. Pensò che intendendo la misura del suono avrebbe rivelato l’ordine autentico degli oscuri fenomeni invisibili. Il nostro pensatore era distante dalle antiche forme di superstizione, e per questo tentò di interpretare in modo razionale la sapienza arcaica. I primitivi pensavano i fenomeni sonori come il confine fra l’impercettibile mondo degli spiriti e il percettibile mondo della natura. Le differenze fra i singoli eventi auditivi erano considerate manifestazioni di forze tenebrose, segnali di un ordine oscuro.
Il pensatore crotonese per primo illuminò l’umanità sul significato immenso che la musica possiede, liberando il suono dalle credenze popolari magiche e dal puro sensoriale.
La grandezza dei seguaci di Pitagora fu di trasformare il pensiero mitico in luminosa razionalità, nel convertire le idee inestensibili in estensibili. Il suono, anima del tempo, si trasformò con Pitagora in galassia spaziale, i suoi fedeli iniziarono a misurarlo e a penetrarlo nei suoi più oscuri recessi, rivelando i fenomeni invisibili delle oscillazioni sonore e li classificarono dentro geometrie ordinate.
Il monocordo (kanon) servì all’avvio della ricerca pitagorica per contrassegnare con un numero le differenti tipologie intervallari, le differenze fra le altezze sonore e le proporzioni armoniche, fra le sonorità generatrici.
Crotone fu la patria delle prime esperienze musicali in senso alto. I rapporti armonici tra le vibrazioni diventarono una scienza. I rapporti aurei della musica, che determinarono l’impalcatura delle scale musicale per oltre duemila anni, furono diretta propagazione della mente del maestro crotonese. Magica divinazione pitagorica, le relazioni di consonanza perfetta prodotte dal pensiero del nostro pensatore sorsero nella serie degli ipertoni molti secoli dopo, quando gli strumenti d’analisi fisica delle sonorità acustiche, rivelarono archeologie profonde e microscopiche. Pitagora cercò il perenne nel fenomeno poco pronunciato.
Il suono è l’elemento più sottile della materia, rendere stimabile ed estensibile la sua risonanza poteva dar ragione della dichiarazione che il numero è il principio fondamentale delle cose. Immaginare la vibrazione nello spazio fu l’invenzione basilare del pensiero pitagorico. Il suono come fenomeno unicamente temporale si sottraeva al controllo razionale. Elaborare uno spazio della musica fu il primo passo verso le forme della musica occidentale.
Per ottenere la misurabilità del suono Pitagora ideò uno strumento molto semplice: il Kanon, in tale maniera chiamato dai greci poiché riproduceva la regola o la ragione intima della materia visibile. Il Kanon o monocordo era costituito da una piccola cassetta rettangolare sormontata da una corda e da un sottostante ponticello mobile che doveva servire a suddividere in porzioni misurabili le parti ondeggianti della corda. Il primo suono che Pitagora ricavò dal monocordo fu ottenuto dividendo la corda in due parti uguali. Pizzicando una delle due parti acquisite dal frazionamento della corda, il pensatore crotonese riuscì ad ottenere un suono simile a quello della corda intera con la differenza di una risonanza più acuta e pungente. Chiamò tale relazione armonia poiché all’interno del rapporto sonoro vi era in uguale misura motivi di concordanza e di contrasto. La ricerca proseguì verso intervalli sempre più piccoli fino alle differenze inudibili. Il monocordo divenne corrispondente al logos, ragione, senso recondito dell’esistente.
Nella concezione pitagorica la musica costituì l’armonia invisibile del mondo e i rapporti fra i suoni e l’evoluzione delle sfere celesti, l’energia dell’anima universale e l’ordine interiore di qualunque singolo soggetto, favilla sulla terra dell’anima universale. L’ascolto degli spazi era nella pratica quotidiana dei pitagorici, una mappa utile a raggiungere la pienezza della salute psichica e fisica.
L’ordine e la misura fra i suoni ricalcano l’ordine cosmico (musica mundana), l’ordine dei sentimenti degli uomini (musica humana), l’ordine della sublime creazione artistica (musica istrumentalis).
 L’articolo riassume 10 filoni di ricerca, basati sullo sviluppo di semplici metodi e modelli, ai quali l’autore ha lavorato negli anni, finalizzati al miglioramento dei processi di project management, problem solving and decision making.
L’articolo riassume 10 filoni di ricerca, basati sullo sviluppo di semplici metodi e modelli, ai quali l’autore ha lavorato negli anni, finalizzati al miglioramento dei processi di project management, problem solving and decision making. 
 Nei giorni scorsi la stampa si è innamorata di un conteggio fatto in Inghilterra, secondo il quale entro il 2013 la ricerca scientifica cinese avrà superato quella statunitense. Quel che si intende dire, in realtà, è che il NUMERO di articoli scientifici pubblicati dai cinesi dovrebbe superare quello degli americani entro quella data. Senza nulla togliere all’impetuosa crescita cinese e al suo immenso potenziale residuo, anche intellettuale, tra le due cose passa una differenza enorme. Agli effetti della vera produzione scientifica, infatti… Paolo Magrassi
Nei giorni scorsi la stampa si è innamorata di un conteggio fatto in Inghilterra, secondo il quale entro il 2013 la ricerca scientifica cinese avrà superato quella statunitense. Quel che si intende dire, in realtà, è che il NUMERO di articoli scientifici pubblicati dai cinesi dovrebbe superare quello degli americani entro quella data. Senza nulla togliere all’impetuosa crescita cinese e al suo immenso potenziale residuo, anche intellettuale, tra le due cose passa una differenza enorme. Agli effetti della vera produzione scientifica, infatti… Paolo Magrassi  Si dice che una funzione è ‘effettivamente computabile’ se i suoi valori possono essere trovati sulla base di un qualche procedimento meccanico. Sebbene sia abbastanza semplice catturare intuitivamente questa idea è tuttavia desiderabile avere una definizione matematica un po’ più rigorosa di questo concetto.
Si dice che una funzione è ‘effettivamente computabile’ se i suoi valori possono essere trovati sulla base di un qualche procedimento meccanico. Sebbene sia abbastanza semplice catturare intuitivamente questa idea è tuttavia desiderabile avere una definizione matematica un po’ più rigorosa di questo concetto. 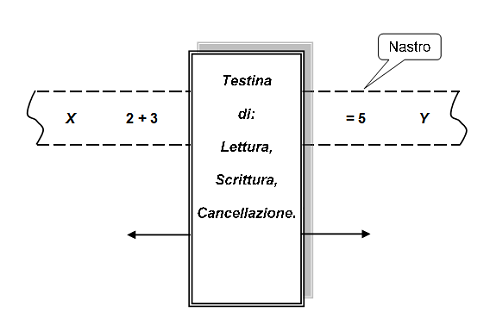
 In questo articolo viene illustrato un algoritmo per il calcolo approssimato di pi greco, con il quale, partendo da un poligono regolare si considera la successione di poligoni regolari dello stesso tipo, ognuno dei quali presenta un numero doppio di lati rispetto al precedente approssimando sempre di più il loro perimetro alle circonferenze dei due cerchi concentrici, uno inscritto nel poligono e l’altro circoscritto al poligono. I poligoni di partenza presi in considerazione sono il triangolo equilatero, il quadrato, il pentagono e l’esagono regolari.
In questo articolo viene illustrato un algoritmo per il calcolo approssimato di pi greco, con il quale, partendo da un poligono regolare si considera la successione di poligoni regolari dello stesso tipo, ognuno dei quali presenta un numero doppio di lati rispetto al precedente approssimando sempre di più il loro perimetro alle circonferenze dei due cerchi concentrici, uno inscritto nel poligono e l’altro circoscritto al poligono. I poligoni di partenza presi in considerazione sono il triangolo equilatero, il quadrato, il pentagono e l’esagono regolari.  Il 4 ottobre 1957 venne lanciato il primo satellite artificiale intorno alla terra, ebbe inizio l’era spaziale e l’opinione pubblica cominciò a conoscere dai mass media i concetti fondamentali della navigazione spaziale ed i termini ad essa relativi, come velocità di fuga, orbita terrestre, satellite geostazionario, ecc. Quanti però conoscono realmente il significato fisico e matematico che si nasconde dietro tali termini?
Il 4 ottobre 1957 venne lanciato il primo satellite artificiale intorno alla terra, ebbe inizio l’era spaziale e l’opinione pubblica cominciò a conoscere dai mass media i concetti fondamentali della navigazione spaziale ed i termini ad essa relativi, come velocità di fuga, orbita terrestre, satellite geostazionario, ecc. Quanti però conoscono realmente il significato fisico e matematico che si nasconde dietro tali termini?  Disponibile gratuitamente il libro di Manara e Lucchini sul pensiero matematico: una raccolta antologica di brani che hanno fatto la storia della matematica e che oggi possono essere di particolare importanza per un insegnamento che tenga presente l’evoluzione di questa scienza. 1. La nascita del matematico: Platone, Euclide, Archimede. 2. Nuovi strumenti per la matematica: Pisano, Cardano, Tartaglia, Bombelli. 3. La nascita della matematica moderna: Galilei, Cartesio, Fermat, Pascal, Newton, Leibnitz. 4. Momenti della matematica moderna: Saccheri, Eulero, Laplace, Fourier, Lobacesvkij, Boole, Cantor, Frege, Klein, Poincaré, Hilbert, Hadamard, Enriques. Il libro è stato pubblicato nel 1976 da U. Mursia Editore. Attualmente è liberamente scaricabile in formato pdf dal sito della Biblioteca matematica dell’UNIMI.
Disponibile gratuitamente il libro di Manara e Lucchini sul pensiero matematico: una raccolta antologica di brani che hanno fatto la storia della matematica e che oggi possono essere di particolare importanza per un insegnamento che tenga presente l’evoluzione di questa scienza. 1. La nascita del matematico: Platone, Euclide, Archimede. 2. Nuovi strumenti per la matematica: Pisano, Cardano, Tartaglia, Bombelli. 3. La nascita della matematica moderna: Galilei, Cartesio, Fermat, Pascal, Newton, Leibnitz. 4. Momenti della matematica moderna: Saccheri, Eulero, Laplace, Fourier, Lobacesvkij, Boole, Cantor, Frege, Klein, Poincaré, Hilbert, Hadamard, Enriques. Il libro è stato pubblicato nel 1976 da U. Mursia Editore. Attualmente è liberamente scaricabile in formato pdf dal sito della Biblioteca matematica dell’UNIMI.  In queste articolo, vengono mostrate alcune applicazioni del software di geometria dinamica Geogebra che permettono simulazioni di ottica geometrica e ondulatoria. Geogebra è un programma gratuito scaricabile da www.geogebra.org. Questo software nelle ultime versioni si è dotato della funzione di animazione delle slider che consente di simulare l’evoluzione temporale di processi fisici.
In queste articolo, vengono mostrate alcune applicazioni del software di geometria dinamica Geogebra che permettono simulazioni di ottica geometrica e ondulatoria. Geogebra è un programma gratuito scaricabile da www.geogebra.org. Questo software nelle ultime versioni si è dotato della funzione di animazione delle slider che consente di simulare l’evoluzione temporale di processi fisici.  Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.
Il cubo di Coppo è una variante del Sudoku inventata da Eugenio Coppo. Le regole sono abbastanza semplici e sono all’interno del file stampabile con il primo cubo che pubblichiamo. Una nuova sfida che sicuramente divertirà chi ama i rompicapo.  "Management significa fare le cose per bene, Leadership significa fare le cose giuste… Ho sempre sottolineato che l’organizzazione non ha nulla a che fare con il potere, ma con la responsabilità" . Peter Drucker (1909-2005).
"Management significa fare le cose per bene, Leadership significa fare le cose giuste… Ho sempre sottolineato che l’organizzazione non ha nulla a che fare con il potere, ma con la responsabilità" . Peter Drucker (1909-2005).  C’è una grande differenza se il capo e il suo potere sono legittimati solo da coloro che lo hanno nominato o vengono invece accettati e riconosciuti, anche dai collaboratori, dai dipendenti, da coloro che vivono nell’ambiente in cui opera. Chi ottiene questo riconoscimento oltre che un manager è anche un leader. Il Leader indica la meta e trasmette a ogni livello dell’organizzazione l’importanza, il valore di ciò che si sta facendo, crea entusiasmo e orgoglio, per cui ciascuno mette a frutto la sua intelligenza e prodiga le sue migliori energie. Il leader non ha paura di scegliere le persone più creative, dotate di autonomia di giudizio perché sa come guidarle. Lo stato maggiore delle grandi imprese di successo è sempre formato da manager di prim’ordine, che il leader tiene costantemente informati e con cui si consulta per le decisioni importanti in un clima di rispetto e di armonia. E’ una costruzione corale di cui lui è il direttore d’orchestra, ma a cui ciascuno contribuisce con la propria abilità. L’impresa diventa allora una comunità a cui tutti sono orgogliosi di appartenere, perché vivono il suo successo come proprio….. Si può imparare a diventare leader? E’ difficile, però si può fare imparando a lavorare in equipe, cioè raccogliendo intorno a se i propri collaboratori , dando loro tutte le informazioni necessarie, discutendo coralmente i problemi e assegnando a ciascuno i suoi compiti e la volta successiva, verificando insieme i risultati… (Cfr. F. Alberoni, C.Sera 20 Sett 2010).
C’è una grande differenza se il capo e il suo potere sono legittimati solo da coloro che lo hanno nominato o vengono invece accettati e riconosciuti, anche dai collaboratori, dai dipendenti, da coloro che vivono nell’ambiente in cui opera. Chi ottiene questo riconoscimento oltre che un manager è anche un leader. Il Leader indica la meta e trasmette a ogni livello dell’organizzazione l’importanza, il valore di ciò che si sta facendo, crea entusiasmo e orgoglio, per cui ciascuno mette a frutto la sua intelligenza e prodiga le sue migliori energie. Il leader non ha paura di scegliere le persone più creative, dotate di autonomia di giudizio perché sa come guidarle. Lo stato maggiore delle grandi imprese di successo è sempre formato da manager di prim’ordine, che il leader tiene costantemente informati e con cui si consulta per le decisioni importanti in un clima di rispetto e di armonia. E’ una costruzione corale di cui lui è il direttore d’orchestra, ma a cui ciascuno contribuisce con la propria abilità. L’impresa diventa allora una comunità a cui tutti sono orgogliosi di appartenere, perché vivono il suo successo come proprio….. Si può imparare a diventare leader? E’ difficile, però si può fare imparando a lavorare in equipe, cioè raccogliendo intorno a se i propri collaboratori , dando loro tutte le informazioni necessarie, discutendo coralmente i problemi e assegnando a ciascuno i suoi compiti e la volta successiva, verificando insieme i risultati… (Cfr. F. Alberoni, C.Sera 20 Sett 2010).  Peter Drucker (Nato in Austria e laureato in diritto internazionale) ha scritto 39 libri e una quantità indefinita di articoli e saggi sul management; i suoi lavori sono eccezionali per la vastità degli argomenti trattati e ammirevoli per la chiarezza espositiva. Le sue prime opere hanno dato un contributo significativo per stabilire ciò che costituisce la pratica del management; i suoi lavori più recenti affrontano la complessità dell’epoca post-industriale descritta, dagli anni 80 in poi, con tutte le sue problematiche gestionali. Per dare una idea del suo pensiero su come affrontare i problemi delle organizzazioni, la via qui seguita è basata su alcuni brani tratti da vari scritti; il lettore interessato potrà approfondire:
Peter Drucker (Nato in Austria e laureato in diritto internazionale) ha scritto 39 libri e una quantità indefinita di articoli e saggi sul management; i suoi lavori sono eccezionali per la vastità degli argomenti trattati e ammirevoli per la chiarezza espositiva. Le sue prime opere hanno dato un contributo significativo per stabilire ciò che costituisce la pratica del management; i suoi lavori più recenti affrontano la complessità dell’epoca post-industriale descritta, dagli anni 80 in poi, con tutte le sue problematiche gestionali. Per dare una idea del suo pensiero su come affrontare i problemi delle organizzazioni, la via qui seguita è basata su alcuni brani tratti da vari scritti; il lettore interessato potrà approfondire:  "Stiamo cominciando a renderci conto che il management stesso è l’istituzione che sta al centro (metafora dell’amministratore delegato come direttore d’orchestra) della nostra società attuale, e che non c’è molta differenza fra la gestione di un business, di una diocesi, di un ospedale, di una università, di un laboratorio di ricerca, di un sindacato, o di una agenzia governativa ….". Economia, politica e management: nuove tendenze nello sviluppo.
"Stiamo cominciando a renderci conto che il management stesso è l’istituzione che sta al centro (metafora dell’amministratore delegato come direttore d’orchestra) della nostra società attuale, e che non c’è molta differenza fra la gestione di un business, di una diocesi, di un ospedale, di una università, di un laboratorio di ricerca, di un sindacato, o di una agenzia governativa ….". Economia, politica e management: nuove tendenze nello sviluppo.  "Sono stato il primo a rendersi conto che il business deve ricercare il proprio fine al di fuori di se stesso, cioè creando e soddisfacendo il cliente. Sono stato il primo a riconoscere il ruolo centrale del processo decisionale; il primo a mettere in rilievo che la struttura segue la strategia e infine il primo a capire, o se non altro il primo a dichiarare, che il management deve essere un ‘Management By Objectives’ che sappia autocontrollarsi". Markers of Management.
"Sono stato il primo a rendersi conto che il business deve ricercare il proprio fine al di fuori di se stesso, cioè creando e soddisfacendo il cliente. Sono stato il primo a riconoscere il ruolo centrale del processo decisionale; il primo a mettere in rilievo che la struttura segue la strategia e infine il primo a capire, o se non altro il primo a dichiarare, che il management deve essere un ‘Management By Objectives’ che sappia autocontrollarsi". Markers of Management.  2) Strettamente collegato al primo è il secondo peccato mortale: ‘attribuire a un nuovo prodotto non il suo prezzo effettivo, ma quello che il mercato riesce a sopportare’. Anche questo errore crea ampi spazi alla concorrenza. E’ una politica sbagliata anche se il prodotto è protetto da un brevetto esclusivo, perché se ha l’incentivo a farlo, non c’è concorrente che non riesca a trovare il modo per aggirare anche il brevetto più blindato …
2) Strettamente collegato al primo è il secondo peccato mortale: ‘attribuire a un nuovo prodotto non il suo prezzo effettivo, ma quello che il mercato riesce a sopportare’. Anche questo errore crea ampi spazi alla concorrenza. E’ una politica sbagliata anche se il prodotto è protetto da un brevetto esclusivo, perché se ha l’incentivo a farlo, non c’è concorrente che non riesca a trovare il modo per aggirare anche il brevetto più blindato …  5) L’ultimo dei peccati mortali è: ‘correre dietro ai problemi e trascurare le opportunità’ … Anche dedicando tutte le proprie energie al ‘problem solving’ , il massimo che si può ottenere è di contenere i danni. Solo le opportunità producono risultati e crescita. E le opportunità sono difficili da trattare e richiedono attenzione tanto quanto i problemi più spinosi. Quindi prima di tutto bisogna metter giù una lista delle opportunità che l’azienda potrebbe trovarsi di fronte …. Solo a questo punto si deve pensare alla lista dei problemi e preoccuparsi di trovare le persone giuste per risolverli".
5) L’ultimo dei peccati mortali è: ‘correre dietro ai problemi e trascurare le opportunità’ … Anche dedicando tutte le proprie energie al ‘problem solving’ , il massimo che si può ottenere è di contenere i danni. Solo le opportunità producono risultati e crescita. E le opportunità sono difficili da trattare e richiedono attenzione tanto quanto i problemi più spinosi. Quindi prima di tutto bisogna metter giù una lista delle opportunità che l’azienda potrebbe trovarsi di fronte …. Solo a questo punto si deve pensare alla lista dei problemi e preoccuparsi di trovare le persone giuste per risolverli".  Nel 1685, Isaac Newton intraprese lo studio del moto di un corpo attraverso un mezzo non viscoso e incompressibile. Scrive nei Principia mathematica philosophiae naturalis: «se in un mezzo rarefatto, composto di particelle uguali disposte liberamente ad uguale distanza l’una dall’altra, si muovono una palla e un cilindro con uguale diametro e con uguale velocità nella direzione nell’asse del cilindro, allora la resistenza della palla sarà la metà di quella del cilindro». Le pagine seguenti inquadrano il problema del profilo aerodinamico, giungendo alla costruzione del modello proposto da Newton e ne descrivono alcune proprietà elementari.
Nel 1685, Isaac Newton intraprese lo studio del moto di un corpo attraverso un mezzo non viscoso e incompressibile. Scrive nei Principia mathematica philosophiae naturalis: «se in un mezzo rarefatto, composto di particelle uguali disposte liberamente ad uguale distanza l’una dall’altra, si muovono una palla e un cilindro con uguale diametro e con uguale velocità nella direzione nell’asse del cilindro, allora la resistenza della palla sarà la metà di quella del cilindro». Le pagine seguenti inquadrano il problema del profilo aerodinamico, giungendo alla costruzione del modello proposto da Newton e ne descrivono alcune proprietà elementari. 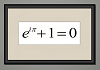 Diciamo spesso che la matematica è bella. Ma pochi ci credono più dell’artista inglese Justin Mullins, che incornicia formule come fossero quadri e ce le fa percepire come solitamente si fruiscono le opere d’arte figurativa. Il suo pezzo più convincente è per me Beauty, riprodotto qui (courtesy Justin Mullins): un quadro che ferma, con perentoria efficacia fotografica, l’identità di Eulero $e^(ipi)+1=0$ per la nostra incondizionata e imperitura ammirazione.
Diciamo spesso che la matematica è bella. Ma pochi ci credono più dell’artista inglese Justin Mullins, che incornicia formule come fossero quadri e ce le fa percepire come solitamente si fruiscono le opere d’arte figurativa. Il suo pezzo più convincente è per me Beauty, riprodotto qui (courtesy Justin Mullins): un quadro che ferma, con perentoria efficacia fotografica, l’identità di Eulero $e^(ipi)+1=0$ per la nostra incondizionata e imperitura ammirazione.  Essendo arrivato alla conclusione che la così detta "partial analysis" non poteva fornire basi sufficientemente ampie per comprendere la struttura e il funzionamento dei sistemi economici, nel 1931 mi sono impegnato a formulare una teoria generale dell’equilibrio economico che fosse utilizzabile praticamente. Nel 1932 ho ricevuto dei fondi di ricerca per l’approntamento della prima tabella input-output dell’economia americana (anni 1919 e 1929). Ho iniziato ad utilizzare le calcolatrici meccaniche nel 1935 e nel 1943 Mark1 (il primo grande calcolatore elettromeccanico)…
Essendo arrivato alla conclusione che la così detta "partial analysis" non poteva fornire basi sufficientemente ampie per comprendere la struttura e il funzionamento dei sistemi economici, nel 1931 mi sono impegnato a formulare una teoria generale dell’equilibrio economico che fosse utilizzabile praticamente. Nel 1932 ho ricevuto dei fondi di ricerca per l’approntamento della prima tabella input-output dell’economia americana (anni 1919 e 1929). Ho iniziato ad utilizzare le calcolatrici meccaniche nel 1935 e nel 1943 Mark1 (il primo grande calcolatore elettromeccanico)…  L’analisi input-output è divenuta oggi uno strumento essenziale per la programmazione economica. Leontief costruisce una matrice, o tabella a doppia entrata (vedi un caso semplificato in figura), che riassume tutte le transazioni di beni o di servizi avvenute nel sistema in un certo periodo, e fornisce quindi una immagine analitica di quel sistema (in genere un’economia nazionale, ma può anche essere una regione o un distretto) in un certo momento e ad un certo grado di sviluppo tecnologico. Questa immagine è caratterizzata dalle relazioni di scambio fra settore e settore, che variano al variare della produzione di ogni singolo settore: lo studio di queste variazioni consente di fare previsioni molto accurate sugli effetti della introduzione di nuove tecnologiche, della fondazione di nuove industrie, ed in genere della strategia economica che si vuole applicare.
L’analisi input-output è divenuta oggi uno strumento essenziale per la programmazione economica. Leontief costruisce una matrice, o tabella a doppia entrata (vedi un caso semplificato in figura), che riassume tutte le transazioni di beni o di servizi avvenute nel sistema in un certo periodo, e fornisce quindi una immagine analitica di quel sistema (in genere un’economia nazionale, ma può anche essere una regione o un distretto) in un certo momento e ad un certo grado di sviluppo tecnologico. Questa immagine è caratterizzata dalle relazioni di scambio fra settore e settore, che variano al variare della produzione di ogni singolo settore: lo studio di queste variazioni consente di fare previsioni molto accurate sugli effetti della introduzione di nuove tecnologiche, della fondazione di nuove industrie, ed in genere della strategia economica che si vuole applicare.  TORINO, 11 MARZO 2011 LINGOTTO, VIA NIZZA 230, 1° PIANO Le scuole della provincia di Torino si sfidano in vista delle Olimpiadi nazionali a squadre (pomeriggio, rampa del Lingotto) Gara per il pubblico a squadre (pomeriggio, corte della Ristorazione) Dal mattino, conferenze e mostre
TORINO, 11 MARZO 2011 LINGOTTO, VIA NIZZA 230, 1° PIANO Le scuole della provincia di Torino si sfidano in vista delle Olimpiadi nazionali a squadre (pomeriggio, rampa del Lingotto) Gara per il pubblico a squadre (pomeriggio, corte della Ristorazione) Dal mattino, conferenze e mostre  Tra gli appassionati di matematica ricreativa sono ben noti gli articoli di Martin Gardner sulla matematica ricreativa. Tra le creazioni rese celebri da Gardner vi sono i cosiddetti “polimini”, figure inventate dal matematico inglese Solomon Golomb che si costruiscono unendo dei quadrati lungo uno dei lati. In questo articolo, intendo trattare una serie di figure costruite in maniera simile ai polimini, ma che seguono altre regole e danno origine a configurazioni molto diverse. L’ideatore di queste figure è mio padre, scomparso da due anni, che le aveva chiamate “PUZZLE” e ne aveva costruite molte, usando diversi materiali.
Tra gli appassionati di matematica ricreativa sono ben noti gli articoli di Martin Gardner sulla matematica ricreativa. Tra le creazioni rese celebri da Gardner vi sono i cosiddetti “polimini”, figure inventate dal matematico inglese Solomon Golomb che si costruiscono unendo dei quadrati lungo uno dei lati. In questo articolo, intendo trattare una serie di figure costruite in maniera simile ai polimini, ma che seguono altre regole e danno origine a configurazioni molto diverse. L’ideatore di queste figure è mio padre, scomparso da due anni, che le aveva chiamate “PUZZLE” e ne aveva costruite molte, usando diversi materiali.  Secchi vince il gadget di Aprile del torneo di scacchi.
Secchi vince il gadget di Aprile del torneo di scacchi.  A che serve la Divina Commedia? E l’Eneide? La Gioconda? La musica? A nulla, ovviamente. Eppure anche un bruto sarebbe disposto a convenire che vale la pena di salvarle, semplicemente in virtù della loro bellezza. Esse dispensano gioia, in modo per certi versi non dissimile da un goal di Maradona o dall’assaggio di un cannolo siciliano fatto a regola d’arte: lo si vede anche guardando le risonanze magnetiche funzionali del cervello umano che mostrano l’attivarsi dei centri del piacere.
A che serve la Divina Commedia? E l’Eneide? La Gioconda? La musica? A nulla, ovviamente. Eppure anche un bruto sarebbe disposto a convenire che vale la pena di salvarle, semplicemente in virtù della loro bellezza. Esse dispensano gioia, in modo per certi versi non dissimile da un goal di Maradona o dall’assaggio di un cannolo siciliano fatto a regola d’arte: lo si vede anche guardando le risonanze magnetiche funzionali del cervello umano che mostrano l’attivarsi dei centri del piacere.  Un fantastico viaggio tra le grandi teorie fisiche del XX secolo: la meccanica quantistica, la relatività ristretta e generale e infine la fisica nucleare. Carlos Fiolshais, già autore del libro "Fisica per tutti: e buon divertimento" riesce ancora una volta a spalancare le porte della scienza moderna a tutti con un libro, mostrandoci un mondo estremamente affascinante in poche pagine.
Un fantastico viaggio tra le grandi teorie fisiche del XX secolo: la meccanica quantistica, la relatività ristretta e generale e infine la fisica nucleare. Carlos Fiolshais, già autore del libro "Fisica per tutti: e buon divertimento" riesce ancora una volta a spalancare le porte della scienza moderna a tutti con un libro, mostrandoci un mondo estremamente affascinante in poche pagine.  "… non ha senso parlare della probabilità di un evento se non in relazione all’insieme di conoscenze di cui una persona dispone. … La probabilità soggettiva è quindi un aiuto per dare un’attendibile misura di ciò che non si può misurare oggettivamente" Bruno De Finetti (1906 – 1985), Filosofia della Probabilità.
"… non ha senso parlare della probabilità di un evento se non in relazione all’insieme di conoscenze di cui una persona dispone. … La probabilità soggettiva è quindi un aiuto per dare un’attendibile misura di ciò che non si può misurare oggettivamente" Bruno De Finetti (1906 – 1985), Filosofia della Probabilità. 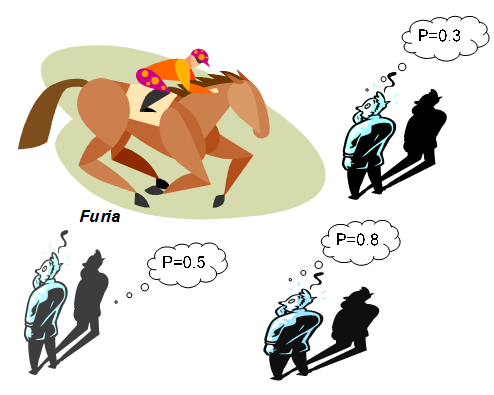
 Una semplice ed interessante esperienza didattica per toccare con mano la p otenza del calcolo matematica. In questo articolo si fa vedere come, partendo da otto piccole fote del satellite Io di Giove si può calcolare la massa di Giove utilizzando la matematica che si studia al liceo.
Una semplice ed interessante esperienza didattica per toccare con mano la p otenza del calcolo matematica. In questo articolo si fa vedere come, partendo da otto piccole fote del satellite Io di Giove si può calcolare la massa di Giove utilizzando la matematica che si studia al liceo.  "… si potrebbe quindi congetturare che questi assiomi e regole d’inferenza siano sufficienti a decidere ogni questione matematica che possa essere formalmente espressa in questi sistemi (Principia Mathematica di Russell, teoria dei sistemi nell’assiomatizzazione di Zermelo o Von Neumann). Verrà mostrato … che non è così, che al contrario esistono nei due sistemi menzionati problemi relativamente semplici della teoria dei numeri che non possono essere decisi sulla base degli assiomi"
"… si potrebbe quindi congetturare che questi assiomi e regole d’inferenza siano sufficienti a decidere ogni questione matematica che possa essere formalmente espressa in questi sistemi (Principia Mathematica di Russell, teoria dei sistemi nell’assiomatizzazione di Zermelo o Von Neumann). Verrà mostrato … che non è così, che al contrario esistono nei due sistemi menzionati problemi relativamente semplici della teoria dei numeri che non possono essere decisi sulla base degli assiomi" 
 Con il presente scritto non si vuole assolutamente mancare di rispetto ad alcuno in un caso di incredibile crudeltà familiare, ma il delitto di Avetrana ci offre l’occasione di parlare di un nuovo concetto della teoria dei giochi, permettendo di sviluppare una soluzione innovativa anche per il ben noto Dilemma del Prigioniero proposto negli anni Cinquanta da Albert Tucker.
Con il presente scritto non si vuole assolutamente mancare di rispetto ad alcuno in un caso di incredibile crudeltà familiare, ma il delitto di Avetrana ci offre l’occasione di parlare di un nuovo concetto della teoria dei giochi, permettendo di sviluppare una soluzione innovativa anche per il ben noto Dilemma del Prigioniero proposto negli anni Cinquanta da Albert Tucker.  Un personaggio importante nella storia della matematica è la governante di casa Riemann, che si abbandonò a una pulizia troppo approfondita nell’appartamento dello studioso dopo la morte di questi avvenuta a soli trentanove anni il 20 luglio 1866. Sette anni prima, Riemann aveva congetturato che per conoscere la distribuzione dei numeri primi occorresse esaminare gli zeri della funzione Zeta introdotta da Eulero
Un personaggio importante nella storia della matematica è la governante di casa Riemann, che si abbandonò a una pulizia troppo approfondita nell’appartamento dello studioso dopo la morte di questi avvenuta a soli trentanove anni il 20 luglio 1866. Sette anni prima, Riemann aveva congetturato che per conoscere la distribuzione dei numeri primi occorresse esaminare gli zeri della funzione Zeta introdotta da Eulero 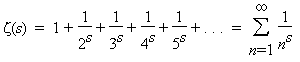
 “Ich bin ein Singularitarian” è il titolo di un capitolo centrale del libro e allo stesso tempo l’affermazione che meglio riassume il messaggio dell’autore. Ray Kurzweil possiede una visione ottimistica e positivista del futuro, derivante probabilmente dalla sua intensa attività in diversi campi di ricerca tecnologica. E’ infatti il fondatore di una società per la ricerca e lo sviluppo di software di riconoscimento vocale, oltre che attivo pensatore e scrittore divulgativo.
“Ich bin ein Singularitarian” è il titolo di un capitolo centrale del libro e allo stesso tempo l’affermazione che meglio riassume il messaggio dell’autore. Ray Kurzweil possiede una visione ottimistica e positivista del futuro, derivante probabilmente dalla sua intensa attività in diversi campi di ricerca tecnologica. E’ infatti il fondatore di una società per la ricerca e lo sviluppo di software di riconoscimento vocale, oltre che attivo pensatore e scrittore divulgativo.  "Ho lottato contro l’idea fissa che esisteva nel mio Paese. Che l’Italia fosse condannata a essere povera per mancanza di fonti energetiche". Enrico Mattei (1906, 1962).
"Ho lottato contro l’idea fissa che esisteva nel mio Paese. Che l’Italia fosse condannata a essere povera per mancanza di fonti energetiche". Enrico Mattei (1906, 1962).  Per mettere in orbita un veicolo spaziale occorre un lanciatore, detto anche vettore, composto da una struttura aerodinamica paragonabile alla fusoliera di un aereo, un sistema di propulsione, un sistema di guida ed il carico di strumentazione. Tutti i moderni razzi sono costruiti in modo che la loro struttura sia integrata con i serbatoi dei propellenti: lo stesso cilindro d’acciaio, o d’alluminio, che contiene i propellenti è anche la struttura attraverso la quale i motori del razzo trasmettono la spinta.
Per mettere in orbita un veicolo spaziale occorre un lanciatore, detto anche vettore, composto da una struttura aerodinamica paragonabile alla fusoliera di un aereo, un sistema di propulsione, un sistema di guida ed il carico di strumentazione. Tutti i moderni razzi sono costruiti in modo che la loro struttura sia integrata con i serbatoi dei propellenti: lo stesso cilindro d’acciaio, o d’alluminio, che contiene i propellenti è anche la struttura attraverso la quale i motori del razzo trasmettono la spinta.  Non lasciatevi ingannare dalla copertina: ”Il matematico in giallo” di Carlo Toffalori,edito da Guanda, non è l’alter ego matematico della signora Fletcher. Infatti, come precisa il sottotitolo “Una lettura scientifica dei romanzi polizieschi”, si tratta di un godibile saggio in cui l’autore si propone di illustrare la relazione tra Matematica e letteratura gialla, che si rivelerà più profonda e interessante di quanto si possa pensare.
Non lasciatevi ingannare dalla copertina: ”Il matematico in giallo” di Carlo Toffalori,edito da Guanda, non è l’alter ego matematico della signora Fletcher. Infatti, come precisa il sottotitolo “Una lettura scientifica dei romanzi polizieschi”, si tratta di un godibile saggio in cui l’autore si propone di illustrare la relazione tra Matematica e letteratura gialla, che si rivelerà più profonda e interessante di quanto si possa pensare.  E chi può dirlo? Miss Italia del ….? L’attrice che, negli ultimi tempi, è contesa da numerose trasmissioni televisive? La ragazza conosciuta la scorsa estate? O forse proprio quella che ti ha colpito … al punto che hai deciso di dividere la tua vita con lei? O quella che .. ? Ci sono anche forme di bellezza ben più astratte …
E chi può dirlo? Miss Italia del ….? L’attrice che, negli ultimi tempi, è contesa da numerose trasmissioni televisive? La ragazza conosciuta la scorsa estate? O forse proprio quella che ti ha colpito … al punto che hai deciso di dividere la tua vita con lei? O quella che .. ? Ci sono anche forme di bellezza ben più astratte …  Simulazione dell’esame ECDL modulo 6: PowerPoint
Simulazione dell’esame ECDL modulo 6: PowerPoint 

 Desideroso di approfondire alcune cose che avevo letto da Odifreddi circa la fortuna di Euclide nella storia, nonché di riprendere, con evidente piglio senile, certi temi che mi furono cari ai tempi della laurea (allora, oltre alla tesi, si compilavano due “tesine” supplementari, e una delle mie era sulle geometrie non euclidee), un paio di anni fa mi sono procurato le uniche due traduzioni italiane di Euclide che, a quanto ne so, siano state realizzate nel secondo dopoguerra: Attilio Frajese e Lamberto Maccioni (a cura di), Gli Elementi di Euclide, UTET, Torino 1970; Fabio Acerbi (a cura di), Euclide. Tutte le opere – Testo greco a fronte, Bompiani, Milano 2007.
Desideroso di approfondire alcune cose che avevo letto da Odifreddi circa la fortuna di Euclide nella storia, nonché di riprendere, con evidente piglio senile, certi temi che mi furono cari ai tempi della laurea (allora, oltre alla tesi, si compilavano due “tesine” supplementari, e una delle mie era sulle geometrie non euclidee), un paio di anni fa mi sono procurato le uniche due traduzioni italiane di Euclide che, a quanto ne so, siano state realizzate nel secondo dopoguerra: Attilio Frajese e Lamberto Maccioni (a cura di), Gli Elementi di Euclide, UTET, Torino 1970; Fabio Acerbi (a cura di), Euclide. Tutte le opere – Testo greco a fronte, Bompiani, Milano 2007.  E’ importantissimo che i vertici delle organizzazioni siano orientati alla qualità. In assenza di manifestazioni di interesse sincere da parte del top management, ai livelli più bassi accadrà ben poco. Per incamminarsi in maniera rivoluzionaria sulla strada del miglioramento occorre che il miglioramento diventi un dovere, una parte del lavoro quotidiano, scritto nel mansionario di ognuno. Joseph Juran (1904-2008).
E’ importantissimo che i vertici delle organizzazioni siano orientati alla qualità. In assenza di manifestazioni di interesse sincere da parte del top management, ai livelli più bassi accadrà ben poco. Per incamminarsi in maniera rivoluzionaria sulla strada del miglioramento occorre che il miglioramento diventi un dovere, una parte del lavoro quotidiano, scritto nel mansionario di ognuno. Joseph Juran (1904-2008). 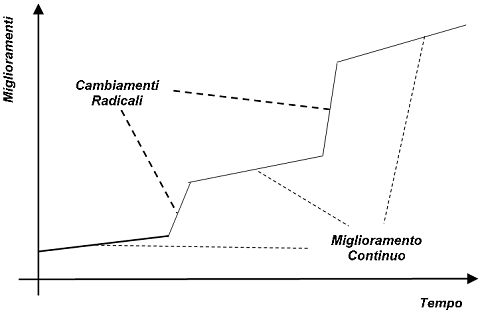
 Workshop internazionale 10-17 aprile 2011, presso ITIS "E.Mattei" di Urbino. Participants will gain knowledge and skills related to: – the theory of prime numbers and the many applications in mathematics, – history of mathematics of the ‘500 and ‘600 – interactions between mathematics and art / literature – specific skills These knowledge and skills can be discharged into the educational and cultural training of participants enriching both who come from specifical areas of mathematics and the ones who belong to sectors artistic / literary / philosophical.
Workshop internazionale 10-17 aprile 2011, presso ITIS "E.Mattei" di Urbino. Participants will gain knowledge and skills related to: – the theory of prime numbers and the many applications in mathematics, – history of mathematics of the ‘500 and ‘600 – interactions between mathematics and art / literature – specific skills These knowledge and skills can be discharged into the educational and cultural training of participants enriching both who come from specifical areas of mathematics and the ones who belong to sectors artistic / literary / philosophical.  I sistemi real-time sono quei sistemi informatici atti a reagire ad eventi esterni entro precisi vincoli temporali. Essi, a differenza degli altri sistemi informatici, non devono limitarsi ad eseguire correttamente le loro funzioni, ma devono anche completarle entro chiari limiti temporali. Il termine real-time (tempo reale) può indurre facilmente a ritenere che tali sistemi siano più veloci degli altri, ma in realtà non è così; infatti, i vincoli temporali a cui essi sono sottoposti possono essere anche intervalli di tempo della durata di molti minuti.
I sistemi real-time sono quei sistemi informatici atti a reagire ad eventi esterni entro precisi vincoli temporali. Essi, a differenza degli altri sistemi informatici, non devono limitarsi ad eseguire correttamente le loro funzioni, ma devono anche completarle entro chiari limiti temporali. Il termine real-time (tempo reale) può indurre facilmente a ritenere che tali sistemi siano più veloci degli altri, ma in realtà non è così; infatti, i vincoli temporali a cui essi sono sottoposti possono essere anche intervalli di tempo della durata di molti minuti.