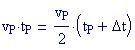|
Scacchi
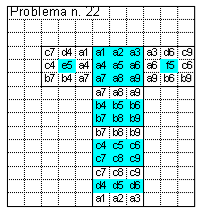
Quante sono le possibili partite di scacchi in cui due giocatori rimangono con un re e un cavallo ciascuno, senza che nessuno dei due pezzi sia immediatamente minacciato?
In altre parole, in quanti modi si possono posizionare su una scacchiera un re bianco e un re nero, un cavallo bianco e un cavallo nero in modo che nessuno dei pezzi sia minacciato da quelli dell’avversario?
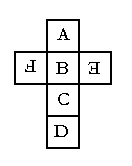
Per chi non conosce il gioco degli scacchi, nella figura sono rappresentate con una croce rossa le caselle minacciate dal re, e con una croce blu le caselle minacciate dal cavallo.
soluzione
|
soluzione
Non è semplice esaminare tutte le posizioni possibili senza far uso di un programma e di un computer. Qualcuno ci è riuscito.
La risposta è 8.282.676.
La soluzione di Cavia (Castelvetro MO)
motivazione: incomunicabile (*)
(*) Per prima cosa ho acquistato una scacchiera magnetica per poter aggredire il problema durante il mio viaggio quotidiano in corriera. Mi è bastato il primo viaggio di andata al lavoro per riconoscere che doveva trattarsi di un numero molto grande, forse dello stesso ordine di grandezza di quello del primo problema sugli euro. A convincermi di ciò è stata la seguente considerazione: mettendo il re bianco in A8 e il cavallo bianco in B8, il re nero, sull’ottava traversa, non può stare nella colonna C e, ovviamente, nemmeno in quelle già occupate; messo in D8 lascia al cavallo nero C8, E8, F8, G8, H8 e … un sacco di altre caselle! Ho pensato allora che avrei dovuto imparare qualcosa di più del gioco degli scacchi per carpire qualche segreto invisibile ai profani. Dopo la lettura di un libro di Fischer per principianti sono passato a Karpov, ma era molto pesante. Molto meglio Capablanca, limpido ed essenziale. Alekhine e Lasker mi hanno spaventato, anche se non come Rubinstein, Tarrasch e Tal. Di Kasparov ho letto d’un fiato “Sfida senza fine”, ma non si parlava quasi per niente di scacchi! Steinitz mi ha chiarito qualche dubbio, ma è stato Petrosjan a farmi schiantare! Sono allora ritornato a Capablanca e in una sua frase ho trovato il segreto della risposta: “.. per i primi dieci anni di attività scacchistica non ho mai letto un solo libro di scacchi …”. Ho così ripreso con me in corriera la scacchierina magnetica e lasciato a casa i libri. Posizionando sistematicamente i primi tre pezzi e contando rapidamente il numero di posizioni del quarto e sfruttando tutte le possibili simmetrie sono arrivato a contare una media di circa 200000 posizioni accettabili ogni viaggio. Rinunciando alla piadina al bar e rimanendo in ufficio con una merenda portata da casa ho continuato a contare posizioni su posizioni anche durante l’intervallo del mezzogiorno, procedendo instancabilmente e implacabilmente fino alla ripresa del lavoro. Risalito in corriera ricominciavo a contare sotto lo sguardo timoroso e sbigottito di una vecchia signora che andava a trovare ogni giorno il nipotino malato. Solo un saluto e via a contare. Questa notte ho completato il calcolo! Ero sicuro che avrei potuto farcela. In fondo il numero di possibilità non poteva superare 64x63x62x61=15249024. Dedico questo risultato al mio nuovo idolo: Capablanca!
F15 EAGLE (S. Giorgio Legnano)
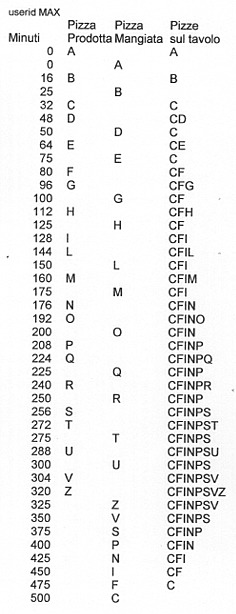
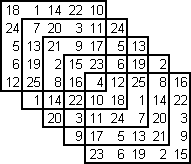
In ciascuna casella della scacchiera (v. tabella allegata) è indicato il numero di disposizioni del Re nero e dei Cavalli bianco e nero che soddisfano le condizioni richieste quando il Re bianco è posizionato in quella casella della scacchiera.
Il risultato è stato determinato sviluppando completamente le posizioni degli altri pezzi quando il Re bianco si trova nelle caselle di coordinate: a1, a2, a3, a4, b2, b3, b4, c3, c4, d4.
Successivamente, per simmetria, sono state completate tutte le altre caselle.
| 8 |
153861 |
141030 |
139168 |
139538 |
139538 |
139168 |
141030 |
153861 |
| 7 |
141030 |
124298 |
120480 |
121042 |
121042 |
120480 |
124298 |
141030 |
| 6 |
139168 |
120480 |
116832 |
117480 |
117480 |
116832 |
120480 |
139168 |
| 5 |
139538 |
121042 |
117480 |
118202 |
118202 |
117480 |
121042 |
139538 |
| 4 |
139538 |
121042 |
117480 |
118202 |
118202 |
117480 |
121042 |
139538 |
| 3 |
139168 |
120480 |
116832 |
117480 |
117480 |
116832 |
120480 |
139168 |
| 2 |
141030 |
124298 |
120480 |
121042 |
121042 |
120480 |
124298 |
141030 |
| 1 |
153861 |
141030 |
139168 |
139538 |
139538 |
139168 |
141030 |
153861 |
|
a |
b |
c |
d |
e |
f |
g |
h |
|
|
|
|
|
|
|
|
|
| parziali |
1147194 |
1013700 |
987920 |
992524 |
992524 |
987920 |
1013700 |
1147194 |
|
|
|
|
|
|
|
|
|
| totale |
8282676 |
|
|
|
|
|
|
|
Robiwood (Borgaro TO)
| A1 |
153861 |
B1 |
141030 |
C1 |
139168 |
D1 |
139538 |
E1 |
139538 |
F1 |
139168 |
G1 |
141030 |
H1 |
153861 |
| A2 |
141030 |
B2 |
124298 |
C2 |
120480 |
D2 |
121042 |
E2 |
121042 |
F2 |
120480 |
G2 |
124298 |
H2 |
141030 |
| A3 |
139168 |
B3 |
120480 |
C3 |
116832 |
D3 |
117480 |
E3 |
117480 |
F3 |
116832 |
G3 |
120480 |
H3 |
139168 |
| A4 |
139538 |
B4 |
121042 |
C4 |
117480 |
D4 |
118202 |
E4 |
118202 |
F4 |
117480 |
G4 |
121042 |
H4 |
139538 |
| A5 |
139538 |
B5 |
121042 |
C5 |
117480 |
D5 |
118202 |
E5 |
118202 |
F5 |
117480 |
G5 |
121042 |
H5 |
139538 |
| A6 |
139168 |
B6 |
120480 |
C6 |
116832 |
D6 |
117480 |
E6 |
117480 |
F6 |
116832 |
G6 |
120480 |
H6 |
139168 |
| A7 |
141030 |
B7 |
124298 |
C7 |
120480 |
D7 |
121042 |
E7 |
121042 |
F7 |
120480 |
G7 |
124298 |
H7 |
141030 |
| A8 |
153861 |
B8 |
141030 |
C8 |
139168 |
D8 |
139538 |
E8 |
139538 |
F8 |
139168 |
G8 |
141030 |
H8 |
153861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Totale: |
|
8282676 |
La soluzione di X (Caltagirone CT)
Motivazione: Riferiamo la scacchiera ad un sistema di riferimento con origine nell’angolo in basso a sinistra. Le caselle possono essere individuate dalle coordinate (x,y) con
x e y appartenenti all’insieme [1 2 3 4 5 6 7 8]
Il numero di modi possibili in cui possono essere posizionati i pezzi sulla scacchiera non considerando le sovrapposizioni (uno o più pezzi possono condividere la stessa casella) e la minaccia di un pezzo da parte di uno di quelli dell’avversario sono:
Ntot=(8*8)^4=(2^3*2^3)^4=(2^6)^4=2^24=16777216
pari al numero di disposizioni con ripetizione di classe k=4 di n=64 elementi.
Da questo numero bisogna sottrarre il numero di volte che 2 o più pezzi risultano sovrapposti. In effetti si può determinare il numero di modi possibili in cui possono essere posizionati i pezzi sulla scacchiera escudendo le sovrapposizioni come il numero di disposizioni di classe k=4 (il numero di pezzi) di n=64 elementi (le caselle) cioè
N1=D(64,4)=64*63*62*61=15249024
Il numero cercato deve essere inferiore a questo in quanto bisogna ancora sottrarre i casi in cui un pezzo è minacciato da un pezzo dell’avversario. Per la sua determinazione ho realizato un semplice programma in Matlab che riporto di seguito.
Ho indicato con Ntot il numero totale di modi in cui uno o più pezzi possono condividere la stessa casella e possono essere minacciati da parte di un pezzo dell’avversario, con N1 il numero di modi possibili in cui i pezzi possono essere posizionati sulla scacchiera escudendo le sovrapposizioni e con N2 il numero soluzione del quesito. In tal modo confronterò risultati numerici con quelli teorici.
Sia inoltre
xrb=coordinata x del re bianco
yrb=coordinata y del re bianco
xrn=coordinata x del re nero
yrn=coordinata y del re nero
xcb=coordinata x del cavallo bianco
ycb=coordinata y del cavallo bianco
xcn=coordinata x del cavallo nero
ycn=coordinata y del cavallo nero
La condizione pezzo_minaccia_pezzo=1 significa che c’è la minaccia pezzo_minaccia_pezzo=0 il contrario. Le condizioni considerate sono state:
r_minaccia_r un re (qualsiasi) minaccia l’altro re
rb_minaccia_cn il re bianco minaccia il cavallo nero
rn_minaccia_cb il re nero minaccia il cavallo bianco
cb_minaccia_rn il cavallo bianco minaccia il re nero
cn_minaccia_rb il cavallo nero minaccia il re bianco
c_minaccia_c un cavallo (qualsiasi) minaccia l’altro cavallo
quando non c’è nessun pezzo minacciato incremento il contatore N2.
*******************************************************************************
Ntot=0;
N1=0;
N2=0;
for xrb=1:8
for yrb=1:8
for xrn=1:8
for yrn=1:8
for xcb=1:8
for ycb=1:8
for xcn=1:8
for ycn=1:8
Ntot=Ntot+1;
if ((xrb==xrn) & (yrb==yrn))…
| ((xrb==xcn) & (yrb==ycn))…
| ((xrb==xcb) & (yrb==ycb))…
| ((xcb==xrn) & (ycb==yrn))…
| ((xcb==xcn) & (ycb==ycn))…
| ((xrn==xcn) & (yrn==ycn)) sovrapposizione=1;
% se è verificata questa condizione almeno due pezzi condividono la stessa casella
% quindi non bisogna procedere
else
N1=N1+1;
% i due re non possono trovarsi in caselle adiacenti
if (abs(xrb-xrn)<=1) & (abs(yrb-yrn)<=1)
r_minaccia_r=1;
else
r_minaccia_r=0;
end
% se il re bianco si trova in una casella adiacente a quella del cavallo nero lo minaccia
if (abs(xrb-xcn)<=1) & (abs(yrb-ycn)<=1)
rb_minaccia_cn=1;
else
rb_minaccia_cn=0;
end
% se il re nero si trova in una casella adiacente a quella del cavallo bianco lo minaccia
if (abs(xrn-xcb)<=1) & (abs(yrn-ycb)<=1)
rn_minaccia_cb=1;
else
rn_minaccia_cb=0;
end
% condizione di minaccia del cavallo bianco sul re nero: un cavallo minaccia un pezzo quando si trova
% una casella più a destra (o sinista) e due caselle più in alto (o basso), oppure quando si trova
% due caselle più a destra (o sinista) e una casella più in alto (o basso). Quindi il valore assoluto della
% differenza delle x deve essere 1 oppure 2 e contemporaneamente il valore assoluto della
% differenza delle y deve essere rispettivamante 2 oppure 1. Pertanto il prodotto deve essere 2
if abs(xcb-xrn)*abs(ycb-yrn)==2
cb_minaccia_rn=1;
else
cb_minaccia_rn=0;
end
% condizione di minaccia del cavallo nero sul re bianco
if abs(xcn-xrb)*abs(ycn-yrb)==2
cn_minaccia_rb=1;
else
cn_minaccia_rb=0;
end
% condizione di minaccia del cavallo bianco sul cavallo nero e viceversa
if abs(xcb-xcn)*abs(ycb-ycn)==2
c_minaccia_c=1;
else
c_minaccia_c=0;
end
% verifica se c’è qualche pezzo minacciato
pezzo_minacciato=r_minaccia_r+…
rb_minaccia_cn+rn_minaccia_cb+…
cb_minaccia_rn+cn_minaccia_rb+…
c_minaccia_c;
% se non c’è nessun pezzo minacciato la disposizione dei pezzi va bene: si può incrementare il contatore
if pezzo_minacciato==0
N2=N2+1;
end
end
end
end
end
end
end
end
end
end
disp([‘Ntot=’, num2str(Ntot)])
disp([‘N1=’, num2str(N1)])
disp([‘N2=’, num2str(N2)])
La soluzione di Roberto (Roma)
Per il calcolo è stato necessario scrivere un programma
in " qbasic " che riporto in allegato.
Le caselle della scacchiera sono state individuate con
un numero di due cifre dove la prima cifra indica la
riga e la seconda la colonna ( da 11 a 88).
RB = posizione del re bianco
CB = posizione del cavallo bianco
RN = posizione del re nero
CN = posizione del cavallo nero
RB1 = casella minacciata dal re bianco
CB1 = casella minacciata dal cavallo bianco
RN1 = casella minacciata dal re nero
CN1 = casella minacciata dal cavallo nero
RB, CB, RN, CN sono sempre diversi tra loro
Per abbreviare i tempi di esecuzione del programma
si sono sfruttate le simmetrie della scacchiera del ciclo
più esterno, quello del re bianco.
E’ bastato calcolare i totali parziali di solo 10 caselle
del re bianco al variare di CN, RN, CB da 11 e 88.
Casella ——> Tot
11 ———— 153.861
22 ———— 124.298
33 ———— 116.832
44 ———— 118.202 ——— T1 = 513.193 da moltiplicare per 4
12 ———— 141.030
13 ———— 139.168
14 ———— 139.538
23 ———— 120.480
24 ———— 121.042
34 ———— 117.480 ——— T2 = 778.738 da moltiplicare per 8
Risultato finale TOT = 513.193 * 4 + 778.738 * 8 = 8.282.676
10 FOR IR = 1 TO 8
20 DATA – 11, – 10, – 9, – 1, 1, 9, 10, 11
30 READ HR(IR)
40 NEXT IR
50 FOR IC = 1 TO 8
60 DATA – 21,- 19, – 12, – 8, 8, 12 , 19, 21
70 READ HC(IC)
80 NEXT IC
90 DATA 11, 12, 13, 14, 22, 23, 24, 33, 34, 44
100 FOR Y =1 TO 10
110 READ RB
120 TP = 0
130 FOR CB = 11 TO 88
140 IF CB MOD 10 = 9 OR CB MOD 10 = 0 THEN 600
150 IF CB = RB THEN 600
160 FOR RN = 1 TO 88
170 IF RN MOD 10 = 9 OR CB MOD 10 = 0 THEN 500
180 IF RN = CB OR RN = RB THEN 500
190 FOR CN = 11 TO 88
200 IF CN MOD 10 = 9 OR CN MOD 10 = 0 THEN 400
210 IF CN = RN OR CN = CB OR CN = RB THEN 400
220 FOR I = 1 TO 8
230 RB1 = RB + HR( I )
240 CB1 = CB + HR( I)
250 IF RN = RB1 OR RN = CB1 OR CN = RB1 OR CN = CB1 THEN 400
260 RN1 = RN + HN ( I )
270 CN1 = CN + HN ( I )
280 IF RB = RN1 OR RB = CN1 OR CB = RN1 OR CB = CN1 THEN 400
290 NEXT I
300 TP = TP +1
400 NEXT CN
500 NEXT RN
600 NEXT CB
610 PRINT " RB = "; RB; TP
620 HY = 8
630 IF RB MOD 11 = 0 THEN HY = 4
640 TOT = TOT + TP * HY
700 NEXT Y
710 PRINT "TOT = "; TOT
800 END
Cialo (Buggiano PT) Un programma in C++
#include<iostream.h>
const N=12; //Dimensioni scacchiera +4
const M=8; //Dimensioni Scacchiera
int S[N][N];
void inizializza(int S[N][N]) {
for (int i=0;i<N;i++)
for (int j=0;j<N;j++)
S[i][j]=5;
for (int i=(N-M)/2;i<(N+M)/2;i++)
for (int j=(N-M)/2;j<(N+M)/2;j++)
S[i][j]=0;
}
void mettiReB(int S[N][N],int i,int j) {
for (int k=i-1;k<i+2;k++)
for (int m=j-1;m<j+2;m++)
if (S[k][m]<5) S[k][m]=4;
S[i][j]=5;
}
void mettiCavB(int S[N][N],int i, int j) {
if (S[i+2][j-1]<4) S[i+2][j-1]=3;
if (S[i+2][j+1]<4) S[i+2][j+1]=3;
if (S[i-2][j-1]<4) S[i-2][j-1]=3;
if (S[i-2][j+1]<4) S[i-2][j+1]=3;
if (S[i+1][j-2]<4) S[i+1][j-2]=3;
if (S[i+1][j+2]<4) S[i+1][j+2]=3;
if (S[i-1][j-2]<4) S[i-1][j-2]=3;
if (S[i-1][j+2]<4) S[i-1][j+2]=3;
if (S[i][j]==0) S[i][j]=5;
}
void mettiCavN(int S[N][N],int i, int j) {
S[i][j]=5;
}
void togliminacciaReN(int S[N][N]) { //Attenzione
for (int i=(N-M)/2;i<(N+M)/2;i++)
for (int j=(N-M)/2;j<(N+M)/2;j++)
if (S[i][j]==2) S[i][j]=0;
}
void minacciaCavN(int S[N][N],int i, int j) {
if (S[i+2][j-1]<1) S[i+2][j-1]=1;
if (S[i+2][j+1]<1) S[i+2][j+1]=1;
if (S[i-2][j-1]<1) S[i-2][j-1]=1;
if (S[i-2][j+1]<1) S[i-2][j+1]=1;
if (S[i+1][j-2]<1) S[i+1][j-2]=1;
if (S[i+1][j+2]<1) S[i+1][j+2]=1;
if (S[i-1][j-2]<1) S[i-1][j-2]=1;
if (S[i-1][j+2]<1) S[i-1][j+2]=1;
}
void minacciaReN(int s[N][N],int k,int m) {
for (int i=k-1;i<k+2;i++)
for (int j=m-1;j<m+2;j++)
if (S[i][j]<2) s[i][j]=2;
}
int conta_libere(int S[N][N]) {
int cont=0;
for (int i=(N-M)/2;i<(N+M)/2;i++)
for (int j=(N-M)/2;j<(N+M)/2;j++)
if (S[i][j]==0 || S[i][j]==1) cont++;
return cont;
}
void togliCavN(int S[N][N], int i, int j) {
S[i][j]=0;
}
void togliCavB(int S[N][N], int k, int m) {
if (S[k][m]==5) S[k][m]=0;
for (int i=(N-M)/2;i<(N+M)/2;i++)
for (int j=(N-M)/2;j<(N+M)/2;j++)
if (S[i][j]==3) S[i][j]=0;
}
void stampa(int S[N][N]) {
for (int i=(N-M)/2;i<(N+M)/2;i++)
for (int j=(N-M)/2;j<(N+M)/2;j++) {
cout << S[i][j];
if (j==(N+M)/2-1) cout << ‘\n’;
}
cout << ‘\n’;
}
main() {
int partite=0;
inizializza(S);
for (int i=(N-M)/2;i<(N+M)/2;i++)
for (int j=(N-M)/2;j<(N+M)/2;j++) {
mettiReB(S,i,j);
for (int k=(N-M)/2;k<(N+M)/2;k++)
for (int m=(N-M)/2;m<(N+M)/2;m++) {
if (S[k][m]==5) continue;
mettiCavB(S,k,m);
minacciaCavN(S,i,j);
for (int p=(N-M)/2;p<(N+M)/2;p++)
for (int q=(N-M)/2;q<(N+M)/2;q++) {
if (S[p][q]>=1) continue;
mettiCavN(S,p,q);
minacciaReN(S,k,m);
partite=partite+conta_libere(S);
cout << partite << ‘\n’;
togliminacciaReN(S);
togliCavN(S,p,q);
minacciaCavN(S,i,j);
}
togliCavB(S,k,m);
}
inizializza(S); //equivale a togliere il ReB
}
cout << partite;
}
Matrix (Teramo)
Ho buttato giu’ questo codice molto velocemente. E’ possibile fare meglio, con tempo, sia in termini di efficienza sia di leggibilità del codice.
Le caselle della scacchiera sono individuate da due coordinate. La casella all’angolo superiore sinistro ha coordinate (1;1) mentre quelle della casella all’angolo inferiore destro sono (8;8).
Il programma inizia attribuendo una posizione al cavallo bianco CB, individuata dalle sue coordinate (xcb;ycb). Utilizzando dei cicli for-next si esauriscono le coordinate possibili (nell’ordine CB-RB-CN-RN).
Le coordinate attaccate dai vari pezzi sono individuate costruendo gli array cb,rb,cn,cn di dimensioni ognuno 12×12 (dimensioni scelte per evitare coordinate di attacco negative). I valori assegnati alle variabili di tali array hanno il seguente significato:
0 casella libera da pezzi e da attacchi
1 casella attaccata
5 casella occupata dal Cavallo Bianco (CB)
6 casella occupata dal Re Bianco (RB)
7 casella occupata dal Cavallo Nero (CN)
8 casella occupata dal Re Nero (RN)
Infine, si controlla se la disposizione dei pezzi e’ ‘ammissibile’, e cioe’ se nessun pezzo attacca gli altri pezzi o occupa la posizione di qualche altro pezzo.
Nella variabile ‘sit’ si accumula il numero di disposizioni analizzate e nella variabile ‘amm’ si accumula il numero di disposizioni ammissibili.
E’ sufficiente analizzare i casi in cui il cavallo bianco occupa il quarto superiore sinistro della scacchiera (o uno qualsiasi degli altri tre). Per simmetria, le disposizioni ammissibili totali si ottengono moltiplicando la variabile ‘amm’ per 4.
——————————————————————————–
‘ dimensionamento array
DIM cb(12, 12), rb(12, 12), cn(12, 12), rn(12, 12)
sit = 0: ‘ NUMERO DI DISPOSIZIONI ANALIZZATE
amm = 0: ‘ NUMERO DI DISPOSIZIONI AMMISSIBILI
FOR xcb = 1 TO 4: ‘ coordinate CAVALLO BIANCO CB
FOR ycb = 1 TO 4
FOR i = 3 TO 10: FOR j = 3 TO 10: cb(i, j) = 0: NEXT j: NEXT i
‘ posizione di CB
cb(xcb + 2, ycb + 2) = 5
‘ posizioni attaccate da CB
cb(xcb + 4, ycb + 1) = 1
cb(xcb + 3, ycb – 0) = 1
cb(xcb + 1, ycb – 0) = 1
cb(xcb – 0, ycb + 1) = 1
cb(xcb – 0, ycb + 3) = 1
cb(xcb + 1, ycb + 4) = 1
cb(xcb + 3, ycb + 4) = 1
cb(xcb + 4, ycb + 3) = 1
FOR xrb = 1 TO 8: ‘ coordinate RE BIANCO RB
FOR yrb = 1 TO 8
FOR i = 3 TO 10: FOR j = 3 TO 10: rb(i, j) = 0: NEXT j: NEXT i
‘ posizione di RB
rb(xrb + 2, yrb + 2) = 6
‘ RB non deve occulare la posizione di CB
IF xrb = xcb AND yrb = ycb THEN sit = sit + 1: GOTO bypass3
‘ posizioni attaccate da RB
rb(xrb + 3, yrb + 2) = 1
rb(xrb + 3, yrb + 1) = 1
rb(xrb + 2, yrb + 1) = 1
rb(xrb + 1, yrb + 1) = 1
rb(xrb + 1, yrb + 2) = 1
rb(xrb + 1, yrb + 3) = 1
rb(xrb + 2, yrb + 3) = 1
rb(xrb + 3, yrb + 3) = 1
FOR xcn = 1 TO 8: ‘ coordinate CAVALLO NERO CN
FOR ycn = 1 TO 8
FOR i = 3 TO 10: FOR j = 3 TO 10: cn(i, j) = 0: NEXT j: NEXT i
‘ posizione di CN
cn(xcn + 2, ycn + 2) = 7
‘ verifica posizione di CN
IF xcn = xcb AND ycn = ycb THEN sit = sit + 1: GOTO bypass2
IF xcn = xrb AND ycn = yrb THEN sit = sit + 1: GOTO bypass2
‘ CB attacca CN
IF cb(xcn + 2, ycn + 2) = 1 THEN sit = sit + 1: GOTO bypass2
‘ RB attacca CN
IF rb(xcn + 2, ycn + 2) = 1 THEN sit = sit + 1: GOTO bypass2
‘ posizioni attaccate da CN
cn(xcn + 4, ycn + 1) = 1
cn(xcn + 3, ycn – 0) = 1
cn(xcn + 1, ycn – 0) = 1
cn(xcn – 0, ycn + 1) = 1
cn(xcn – 0, ycn + 3) = 1
cn(xcn + 1, ycn + 4) = 1
cn(xcn + 3, ycn + 4) = 1
cn(xcn + 4, ycn + 3) = 1
‘ CN attacca RB
IF cn(xrb + 2, yrb + 2) = 1 THEN sit = sit + 1: GOTO bypass1
FOR xrn = 1 TO 8: ‘ coordinate RE NERO RN
FOR yrn = 1 TO 8
FOR i = 3 TO 10: FOR j = 3 TO 10: rn(i, j) = 0: NEXT j: NEXT i
‘ posizione di RN
rn(xrn + 2, yrn + 2) = 8
sit = sit + 1
‘ verifica posizione di RN
IF xrn = xcn AND yrn = ycn THEN GOTO bypass1
IF xrn = xcb AND yrn = ycb THEN GOTO bypass1
IF xrn = xrb AND yrn = yrb THEN GOTO bypass1
‘ CB attacca RN
IF cb(xrn + 2, yrn + 2) = 1 THEN GOTO bypass1
‘ RB attacca RN
IF rb(xrn + 2, yrn + 2) = 1 THEN GOTO bypass1
‘ posizioni attaccate da RN
rn(xrn + 3, yrn + 2) = 1
rn(xrn + 3, yrn + 1) = 1
rn(xrn + 2, yrn + 1) = 1
rn(xrn + 1, yrn + 1) = 1
rn(xrn + 1, yrn + 2) = 1
rn(xrn + 1, yrn + 3) = 1
rn(xrn + 2, yrn + 3) = 1
rn(xrn + 3, yrn + 3) = 1
‘ RN attacca CB
IF rn(xcb + 2, ycb + 2) = 1 THEN GOTO bypass1
‘ LA SITUAZIONE ANALIZZATA HA SUPERATO TUTTE LE CONDIZIONI *******
amm = amm + 1: ‘ la posizione e’ ammissibile
bypass1:
NEXT yrn
NEXT xrn
bypass2:
NEXT ycn
NEXT xcn
bypass3:
NEXT yrb
NEXT xrb
NEXT ycb
NEXT xcb
PRINT "disposizioni ammissibili : ";amm* 4
STOP
END
Molti altri programmi mi sono pervenuti in diversi linguaggi. Ho pubblicato solo i primi che mi sono arrivati.
 MatematiCup è la prima gara completamente on-line riservata a studenti delle scuole medie. La competizione è organizzata da Matematicamente.it in collaborazione con il DIDA-Lab dell'Università del Salento, Kataweb.it e Repubblica.it, con il patrocinio della Mathesis (Associazione nazionale degli insegnanti di matematica) e del Ministero della Pubblica Istruzione. L'edizione dello scorso anno ha visto il coinvolgimento di 5000 studenti, organizzati in più di 200 squadre, appartenenti a 128 differenti istituti scolastici. Tutti gli alunni, si sono trovati l'8 maggio alle ore 9 contemporaneamente davanti ai monitor per sfidarsi a colpi di operazioni e ragionamenti logici. Dopo tre ore di click sulla tastiera, disegni e calcoli sul quaderno, discussioni animate e sana collaborazione, la squadra migliore è risultata "L’esercito di Franca", guidata dalla professoressa Franca Panelli, della scuola Beato Arnaldo da Limena di Limena, provincia di Padova. Nella classifica generale delle migliori scuole, la prima classificata è stata la Leonardo da Vinci di Cavallino, provincia di Lecce.
MatematiCup è la prima gara completamente on-line riservata a studenti delle scuole medie. La competizione è organizzata da Matematicamente.it in collaborazione con il DIDA-Lab dell'Università del Salento, Kataweb.it e Repubblica.it, con il patrocinio della Mathesis (Associazione nazionale degli insegnanti di matematica) e del Ministero della Pubblica Istruzione. L'edizione dello scorso anno ha visto il coinvolgimento di 5000 studenti, organizzati in più di 200 squadre, appartenenti a 128 differenti istituti scolastici. Tutti gli alunni, si sono trovati l'8 maggio alle ore 9 contemporaneamente davanti ai monitor per sfidarsi a colpi di operazioni e ragionamenti logici. Dopo tre ore di click sulla tastiera, disegni e calcoli sul quaderno, discussioni animate e sana collaborazione, la squadra migliore è risultata "L’esercito di Franca", guidata dalla professoressa Franca Panelli, della scuola Beato Arnaldo da Limena di Limena, provincia di Padova. Nella classifica generale delle migliori scuole, la prima classificata è stata la Leonardo da Vinci di Cavallino, provincia di Lecce. 



 Qual è la formula più bella? I risultati del sondaggio tra i visitatori di questo sito al 31 agosto 2007. Al primo posto al formula di Eulero, al secondo il frattale di Mandelbrot e al terzo il teorema di Pitagora. Tra le ultime l'equivalenza tra massa ed energia di Einstein: E=mc2.
Qual è la formula più bella? I risultati del sondaggio tra i visitatori di questo sito al 31 agosto 2007. Al primo posto al formula di Eulero, al secondo il frattale di Mandelbrot e al terzo il teorema di Pitagora. Tra le ultime l'equivalenza tra massa ed energia di Einstein: E=mc2.









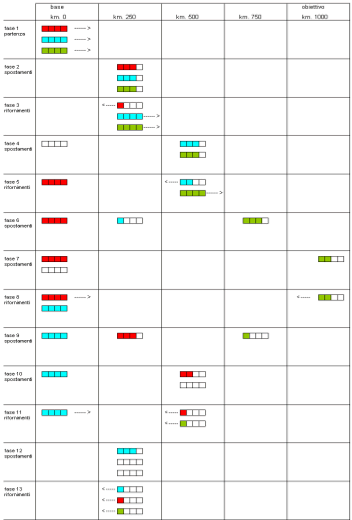
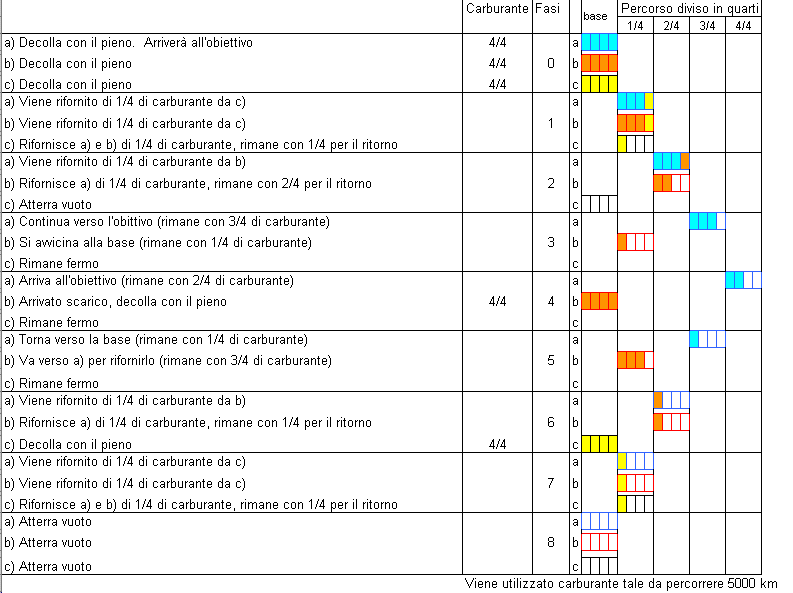 Ucando (Gallarate) 3 aerei
Ucando (Gallarate) 3 aerei 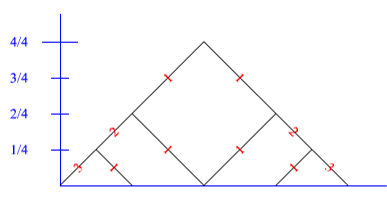
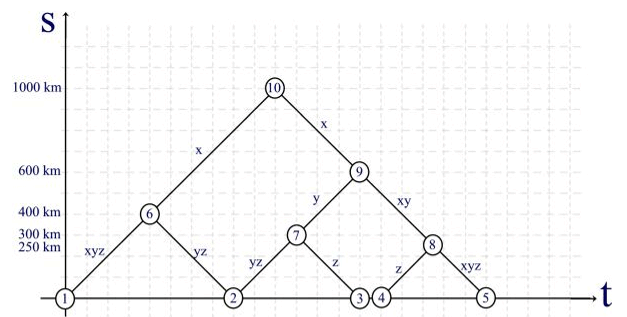
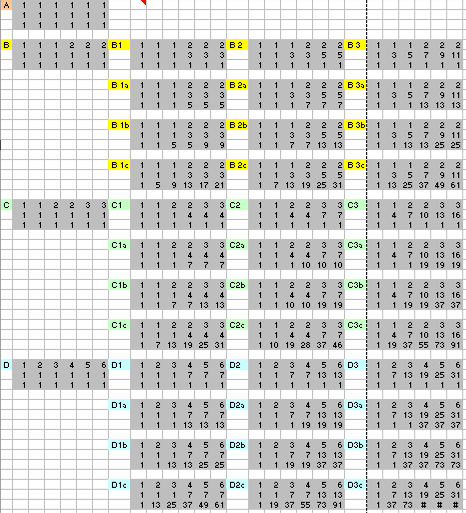


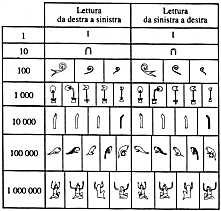
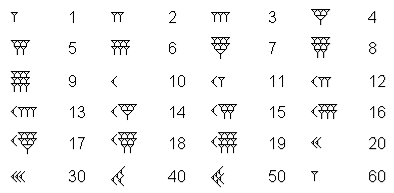




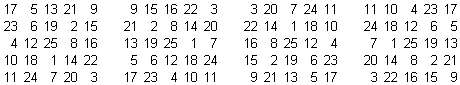

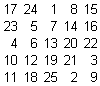
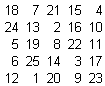

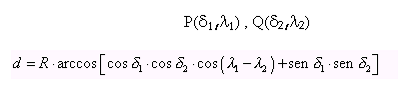
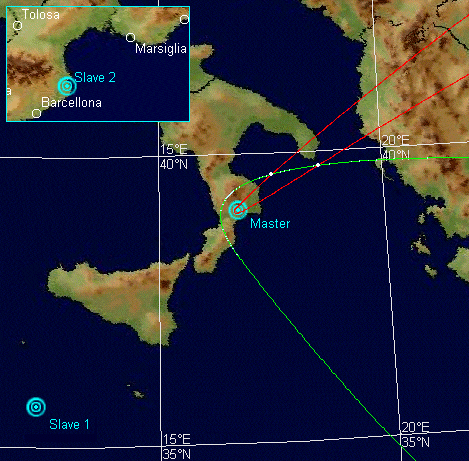
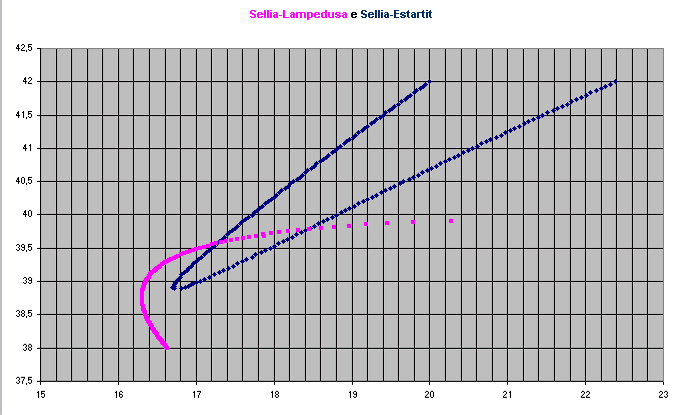
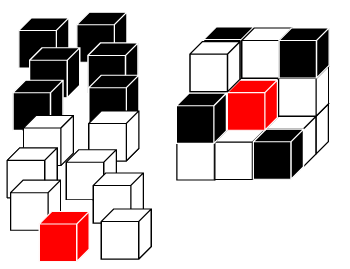

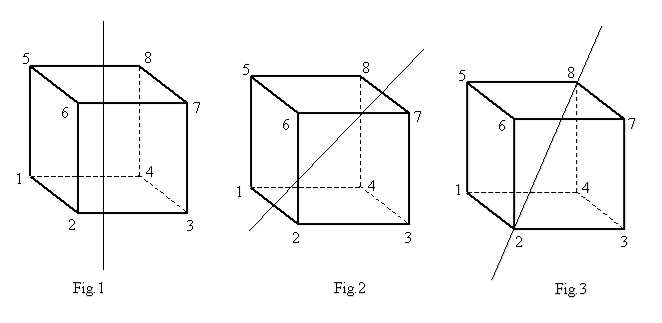


 Per rappresentare la Terra e orientarsi sulla sua superficie si usano le linee dei meridiani e dei paralleli. Sulle prime si misura la latitudine, sulle seconde la longitudine.
Per rappresentare la Terra e orientarsi sulla sua superficie si usano le linee dei meridiani e dei paralleli. Sulle prime si misura la latitudine, sulle seconde la longitudine.

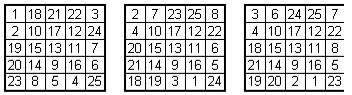
 Nel riquadro centrale devono essere inseriti tutti i numeri interi da 1 a 52 con un'unica condizione da rispettare: ogni numero inserito in una colonna non può essere la somma di altri due numeri della stessa colonna.
Nel riquadro centrale devono essere inseriti tutti i numeri interi da 1 a 52 con un'unica condizione da rispettare: ogni numero inserito in una colonna non può essere la somma di altri due numeri della stessa colonna.