Scarica il file in formato XLS
Autore: Antonio Bernardo
Confronto capitalizzazione semplice-composta
Scarica il file in formato XLS
Lettera per la richiesta di materiali per il laboratorio di scrittura
|
Lettera per la richiesta di materiali per il laboratorio di scrittura
Il laboratorio di scrittura "Il Drago" deve realizzare un giornalino scolastico e ha bisogno di richiedere alcuni materiali al dirigente scolastico. E’ d’obbligo impostare una bella lettera con Word. Il testo da scrivere sia il seguente:
Il sottoscritto, responsabile del Laboratorio di Scrittura "Il Drago", fa presente che per realizzare il Giornalino Scolastico necessita dei seguenti materiali: 5 risme di fogli A4 10 pennarelli neri 5 confezioni di matite colorate 20 penne nere 5 penne rosse 5 confezioni di floppy disk 3,5 pollici 10 CD-Rom 5 cartucce colore per stampante Epson Stylus C60 Le attività saranno svolte nel laboratorio di informatica secondo il seguente calendario: martedì 11/03 dalle 15:00 alle 18:00 giovedì 13/03 dalle 15:00 alle 18:00 martedì 18/03 dalle 15:00 alle 18:00 giovedì 20/03 dalle 15:00 alle 18:00 martedì 22/04 dalle 15:00 alle 18:00 giovedì 24/04 dalle 15:00 alle 18:00 In attesa di riscontro si porgono distinti saluti.
Apri Microsoft Word. Imposta una carta da lettera intestata. Allineato a sinistra inserisci il logo del Laboratorio di scrittura: Inserisci / Immagine / Da file… cerca il file del logo.
Dopo aver inserito il logo vai a capo, scrivi l’intestazione del laboratorio, seleziona il testo per formattarlo.
Come font del carattere puoi scegliere il Tahoma, colore verde scuro, grassetto, dimensione 12.
Vai a capo con il tasto "Invio", imposta il margine sinistro a 10 cm. spostando il rettangolino del righello, il font a Times New Romans, il colore nero, elimina il grassetto, scrivi il destinatario.
Riporta il rettangolino del righello a 0, lascia un rigo bianco, scrivi la data, lascia un rigo bianco, scrivi l’oggetto in grassetto, lascia un altro rigo bianco, scrivi la prima parte della lettera.
Imposta un tabulatore a 8 cm. facendo clic con il mouse sul righello dov’è il numero 8. Dopo aver scritto Descrizione spostati con il tasto tab
Seleziona il rigo Descrizione – Quantità e imposta il carattere Grassetto e Sottolineato. Continua a scrivere il testo della lettera. Poi inserisci una tabella di 3 colonne , 7 righe , con opzione Adatta al contenuto .
Riempi le celle della tabella muovendoti con i l tasto Tab
|
Creare un quiz con PowerPoint
|
Quiz con PowerPoint
Ecco come creare un simpatico gioco con PowerPoint. Scegli il tema del quiz. Per questo esempio si è scelto il tema "Conosci le città d’Italia?". Effettua una ricerca su Internet per procurarti immagini e suoni. Una cartina d’Italia, una gif animata di un cronometro, un certo numero di immagini significative di città italiane e un po’ di musica. Per esempio sul motore di ricerca Google (www.google.it ) seleziona Immagini e cerca le varie immagini
Alcuni siti dove cercare una gif animata: http://www.sempregrafica.com/gif/ Puoi scaricare da qui i file che ti occorrono (cartella compressa 436 KB) Apri PowerPoint. Per la prima diapositiva scegli un layout Titolo e contenuto
Come titolo scrivi: Conosci le città d’Italia? Fai clic sull’icona dell’immagine per inserire l’immagine dell’Italia, selezionandola dalla cartella dove hai salvato le immagini.
La prima diapositiva è pronta.
Rimane da fissare l’effetto di transizione alla diapositiva successiva: dalla barra dei menu selezionare in sequenza Presentazione / Transizione diapositiva… Impostare l’avanzamento di diapositiva sia con un clic del mouse sia automaticamente dopo 00.05 secondi, applicare l’effetto solo alla diapositiva attuale.
Fare clic sul pulsante nuova diapositiva . Per la seconda diapositiva scegli il layout Titolo, testo e contenuto :
Come titolo scrivi Hai 15 secondi per rispondere . A sinistra del titolo inserisci la gif animata del cronometro. A destra clicca sull’icona dell’immagine e inserisci l’immagine di una città. Nell’elenco puntato a sinistra inserisci i nomi di alcune città, tra le quale deve ovviamente esserci il nome della città raffigurata. In basso a destra aggiungi una casella di testo dove scriverai: hai totalizzato finora 0 punti .
Imposta la transizione diapositiva in questo modo: togli la spunta da Con un clic del mouse , metti la spunta su Automaticamente dopo e fissa come tempo 00.15.
Inserisci una nuova diapositiva con layout diapositiva titolo . Come titolo scrivi Tempo scaduto , come sottotitolo Ricomincia il gioco . Per impostare lo sfondo della diapositiva, fai clic con il tasto destro del mouse sulla diapositiva. Dal menu contestuale seleziona Sfondo … , fai clic sulla lista dei colori e scegli Effetti di riempimento .
Nella sezione Colori scegli due colori , nella sezione Sfumatura scegli dal titolo , quindi scegli due colori adatti, clicca su OK e su Applica . Imposta un colore opportuno per la scritta Tempo scaduto.
Imposta la transizione diapositiva in questo modo: togli la spunta da Con un clic del mouse e anche da Automaticamente dopo . In questo modo la transizione alla diapositiva successiva può avvenire solo con un collegamento ipertestuale. Utilizzando i bottoni in basso a sinistra attiva la Visualizzazione sequenza diapositive . Seleziona le diapositive 2 e 3. Copia e incolla le due diapositive tante volte quante sono le domande che si vogliono fare.
A questo punto è il caso di cominciare a salvare il lavoro in una cartella opportuna. In seguito ricorda di salvare di tanto in tanto il file. Modifica le immagini, inserendo quelle delle altre città e modifica la scritta hai totalizzato 0 punti, aumentando ogni volta di un punto. Inserisci una nuova diapositiva con layout diapositiva titolo. Scrivi come titolo Bravo hai completato il gioco , come sottotitolo hai totalizzato 7 punti , se le domande sono sette. Inserisci una nuova diapositiva con layout diapositiva titolo. Scrivi come titolo Fine del gioco , come sottotitolo ricomincia . Ora le diapositive ci sono tutte, bisogna fissare i collegamenti ipertestuali. Seleziona il nome della prima città e premi il bottone del Collegamento ipertestuale , nella finestra che si apre seleziona Inserisci nel documento .
Se il nome della città è corretto collega con la diapositiva 4, come nella figura di sopra. Se il nome della città è errato collega con l’ultima diapositiva, come nella figura di sotto.
Nella diapositiva Tempo scaduto, collega la parola Ricomincia il gioco con la prima diapositiva. Verifica che nella sezione avanzamento diapositiva sia tolta la spunta sia a Con un click del mouse sia a Automaticamente dopo i n modo che dalla diapositiva si possa uscire solo dal collegamento ipertestuale. Collega allo stesso modo tutte le diapositive con le domande: se la risposta è esatta attiva il collegamento con la domanda seguente, se la risposta è errata attiva il collegamento con l’ultima diapositiva di fine gioco. Nell’ultima diapositiva, collega la risposta corretta con la diapositiva "Bravo hai completato il gioco …"
Infine collega la scritta "Ricomincia" con la prima diapositiva.
La presentazione può essere salvata con estensione .ppt, se deve essere ancora modificata, con estensione .pps se deve essere solo eseguita e non si vuole diffondere la costruzione del file: dalla barra dei menu seleziona File / Salva con nome , nella finestra che appare scegli come Tipo file : Presentazione di PowerPoint .
Le due icone hanno aspetto differente
La presentazione può anche essere esportata su un CD-Rom per poterla eseguire anche su computer sprovvisti di PowerPoint. Dalla barra dei menu seleziona File / Presentazione portatile : si avvierà un percorso guidato per esportare ciò che serve.
La procedura è stata descritta per la versione XP di PowerPoint, per le versioni precedenti i passaggi sono del tutto analoghi. Per rendere veramente multimediale la presentazione non resta che inserire un po’ di musica, il tic tic dell’orologio, l’applauso e qualche altro suono. Se non ne hai scaricali da qui .
Scarica il quiz già pronto in PowerPoint (.ppt 435 KB) Scarica il quiz in formato presentazione (.pps 435 KB)
Bernardo |
Creare un sommario con Word
|
Creare un sommario per un documento di Word In un documento lungo e articolato può essere utile per chi scrive e soprattutto per chi legge creare automaticamente un indice che rinvii direttamente al paragrafo desiderato. Questa funzione si ottiene generando un sommario. Apri il documento già scritto e posizionati nel punto in cui vuoi inserire il sommario, di solito all’inizio del documento dopo la eventuale copertina.
Dopo aver scritto INDICE inserisci un’interruzione di pagina: dalla barra dei menu seleziona Inserisci / Interruzione / Di pagina . In questo modo l’indice farà parte di una pagina a sé.
Ripercorri il testo, seleziona il titolo del paragrafo e assegnagli lo stile Titolo 1 .
Se il testo contiene un sottoparagrafo usa lo stile Titolo 2 .
Continuare in questo modo per tutto il documento.
Posizionarsi all’inizio del documento nel punto in cui deve essere inserito il sommario. Dalla barra dei menu selezionare Inserisci / Riferimento / Indici e sommario .
Dalla finestra Indici e sommario , scegli la scheda Sommario. Scegli tra le varie opzioni, in particolare il numero di livelli per i titoli e spunta la casella Usa collegamenti ipertestuali .
Premi OK e il sommario è pronto. Se vuoi puoi modificare la formattazione del testo, usando gli usuali metodi di formattazione.
Soffermandosi un attimo con il puntatore del mouse sull’indice comparirà il messaggio CTRL + clic per aprire il collegamento, in altre parole premendo il tasto Ctrl e facendo clic con il tasto sinistro del mouse ci si sposta automaticamente nel punto indicato.
Può essere utile informare il lettore di questa possibilità scrivendo il messaggio nell’indice. Se si modifica il testo, l’aggiornamento dell’indice si ottiene attivando la barra degli strumenti Struttura da Visualizza / Barre degli strumenti / Struttura e premendo il pulsante Aggiorna sommario .
Può essere utile agevolare il lettore inserendo nel testo dei rimandi all’indice, in modo che finito di leggere un paragrafo possa ritornare all’indice e sceglierne un altro. Inserisci un segnalibro nella parola INDICE: seleziona la parola, dalla barra dei menu seleziona Inserisci / Segnalibro…
Scrivi nella finestra che si apre il nome da assegnare al segnalibro, in questo caso può essere indice .
Dopo aver aggiunto il segnalibro, spostati alla fine di ogni capitolo (puoi utilizzare i link ipertestuali) e allineato a destra scrivi la parola da utilizzare per il rimando all’indice, può essere indice o torna all’indice . Seleziona la parola e premi il pulsante Inserisci collegamento ipertestuale .
Nella finestra che si apre seleziona la voce Inserisci nel documento , cerca tra i segnalibri indice . Il collegamento può essere fatto anche con Inizio documento che compare automaticamente: questa possibilità non è comoda se il documento non comincia con l’indice.
Premi il pulsante OK e la parola apparirà sottolineata in blu. Utilizza il nuovo collegamento ipertestuale per tornare all’indice, spostarti alla fine di un altro capitolo e inserire un nuovo rimando all’indice.
Bernardo |
Creare etichette con Word
|
Stampare le etichette con Word 2002 |
Nel lavoro d’ufficio, ma anche in casa, può capitare di dover inviare lettere, inviti, auguri a un gran numero di persone. E’ utile acquistare delle etichette adesive sulle quali stampare gli indirizzi da un elenco. Vediamo come ottenere un buon risultato con Word 2002.
La funzione che si utilizza viene detta stampa unione . Si crea il documento principale che contiene il foglio con le etichette e un file con gli indirizzi, quindi si uniscono i due file.
Apri un documento vuoto con Word 2002. Dalla Barra dei menu seleziona Strumenti / Lettere e indirizzi / Creazione guidata stampa unione .
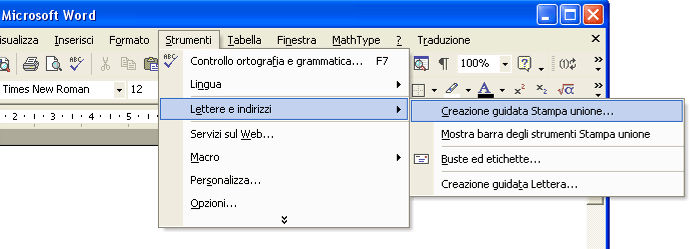
A destra comparirà una sezione per la creazione guidata.
Passo 1 . Spunta l’opzione Etichette e vai al passaggio successivo.
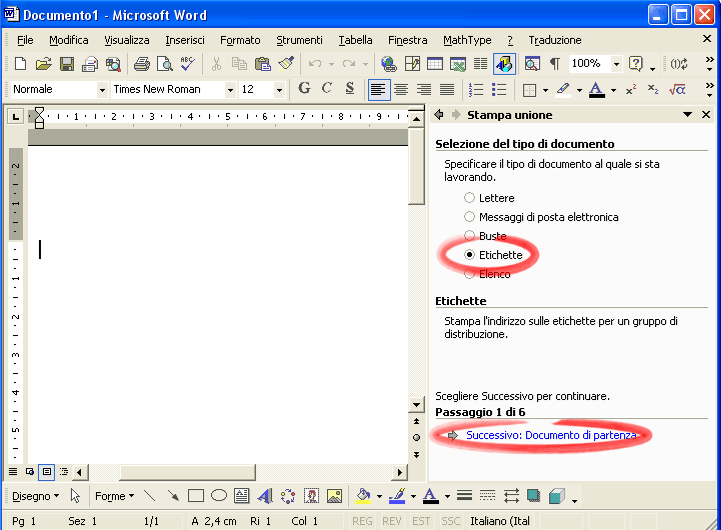
Passo 2 . Scegli Cambia il layout del document o e fai clic su Opzioni etichette per impostare il tipo di etichette.
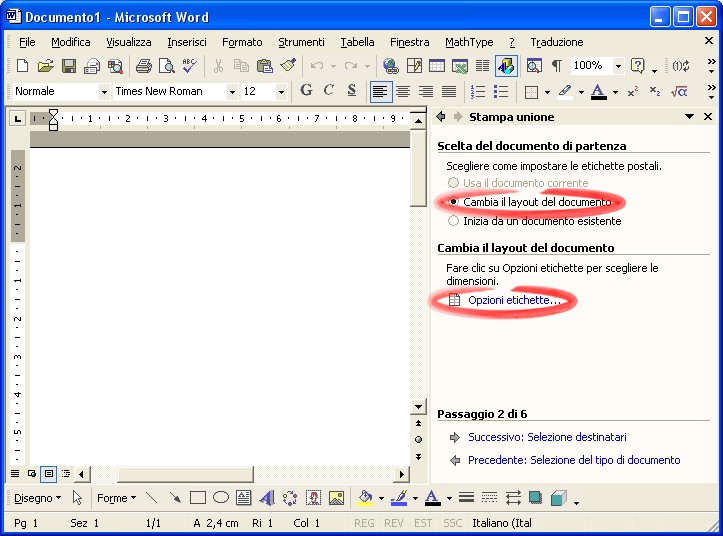
Nella finestra che appare occorre impostare il tipo di etichette che si stanno usando. Imposta il tipo di stampante (Ad aghi o Laser ed a getto d’inchiostro ), scegli il tipo di Etichette dall’omonima lista. Word è predisposto per un gran numero di etichette adesive diffuse in commercio. Se le etichette che hai acquistato non compaiono in elenco scegli Altre/Personalizza .
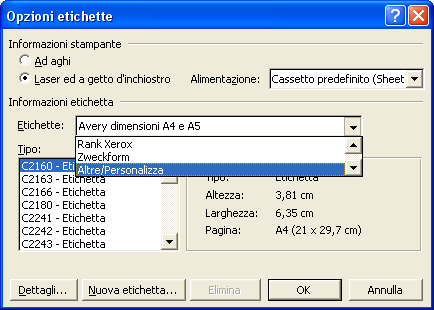
Scegli dall’elenco Tipo il tipo di etichetta. Il bottone Dettagli… ti permette di controllare se il tipo di etichette scelto corrisponde a quello che devi usare. Se non trovi l’etichetta giusta puoi costruirne un tipo nuovo premendo il bottone Nuova etichetta…
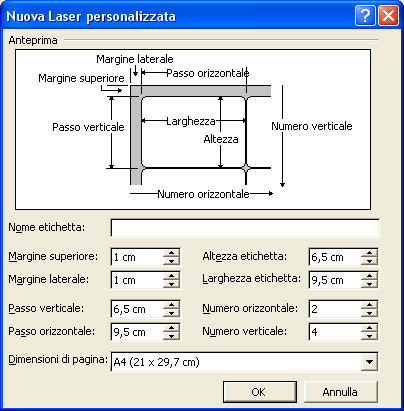
Premere il bottone OK . Il foglio viene impostato in forma di tabella.
Se vuoi visualizzare i bordi della tabella e vedere se corrispondono alle etichette in uso seleziona dalla Barra dei menu la voce Tabella / Proprietà tabella… Dalla finestra che si apre clicca sul bottone Bordi e sfondo… Dalla finestra Bordi e sfondo scegli Tutti , quindi scegli lo Stile , il Colore e lo Spessore : può essere utile scegliere lo stile punteggiato, un colore grigio chiaro e uno spessore piccolo.
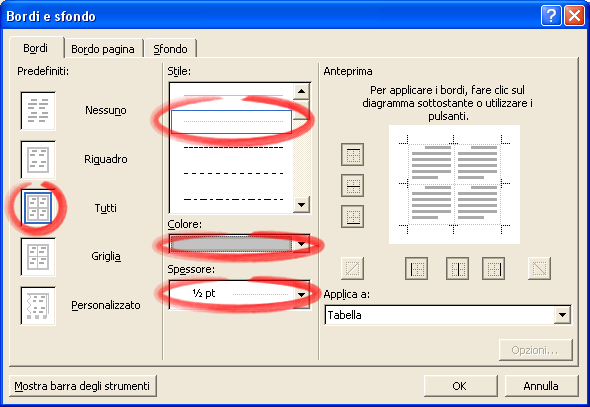
Potrai così vedere il foglio suddiviso nelle varie etichette:
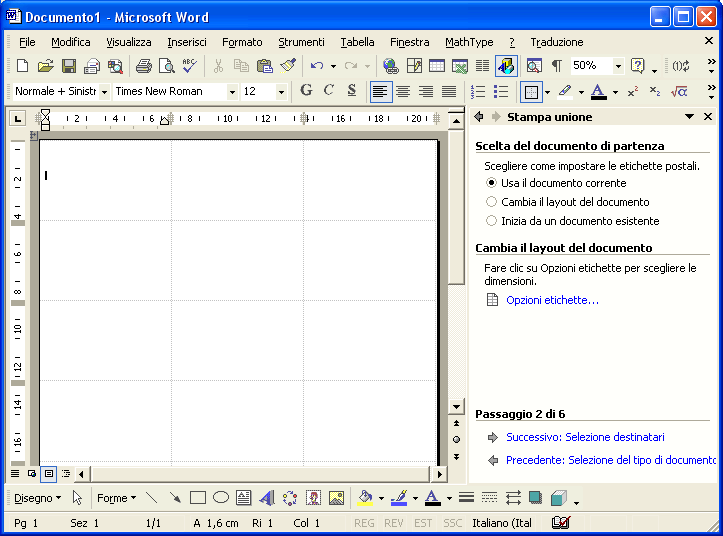
Passo 3 . Fai clic sul passo successivo: Selezione destinatari .
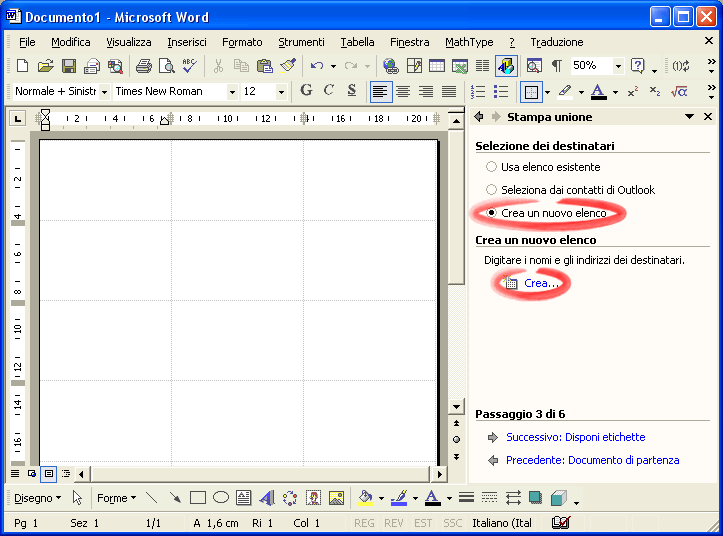
Se il file degli indirizzi è già stato creato spunta la voce Usa elenco esistente , quindi dalla voce Sfoglia cerca il file che contiene gli indirizzi. Se il file con gli indirizzi non esiste devi crearlo: spunta la voce Crea un nuovo elenco e fai clic su Crea . Si apre la finestra Nuovo elenco indirizzi nella quale si inseriscono le voci che interessano. Alla fine di ogni indirizzo premi il bottone Nuova voce .
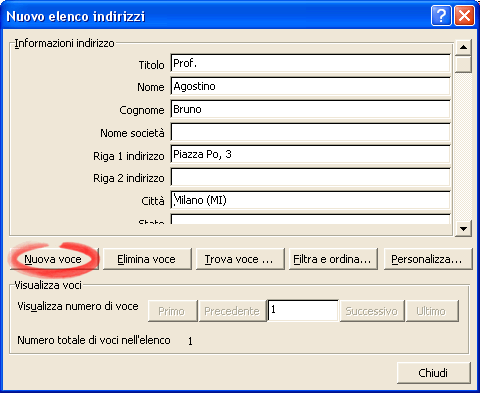
Quando hai inserito tutti gli indirizzi premi il tasto Chiudi . A questo punto ti viene chiesto il nome del file degli indirizzi e dove salvarlo. Il file ha estensione .mdb, estensione tipica dei data base, e viene salvato per default nella cartella Origini dati utente; questa cartella può chiaramente essere cambiata.
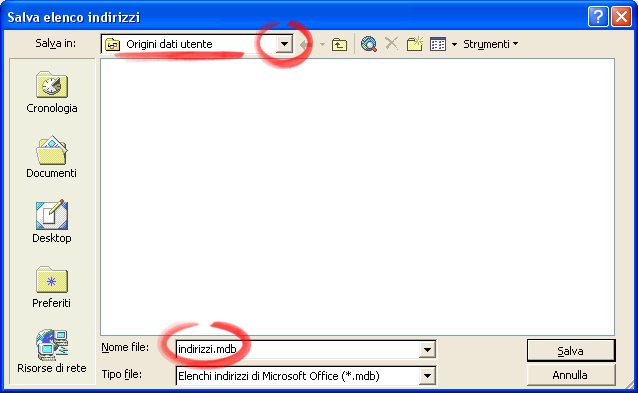
Si apre la finestra Destinatari Stampa unione dalla quale è possibile apportare delle modifiche al database e indicare quali indirizzi devono essere stampati, spuntando la relativa riga Quindi premere OK.
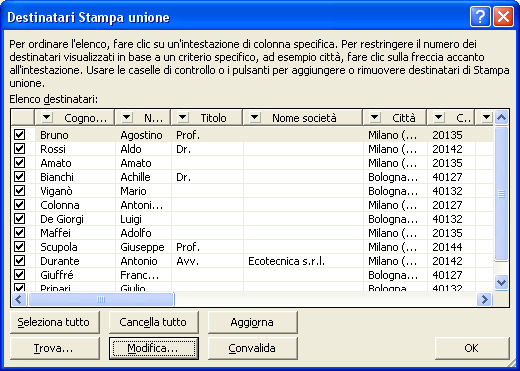
Fai clic su Successivo: Disponi etichette
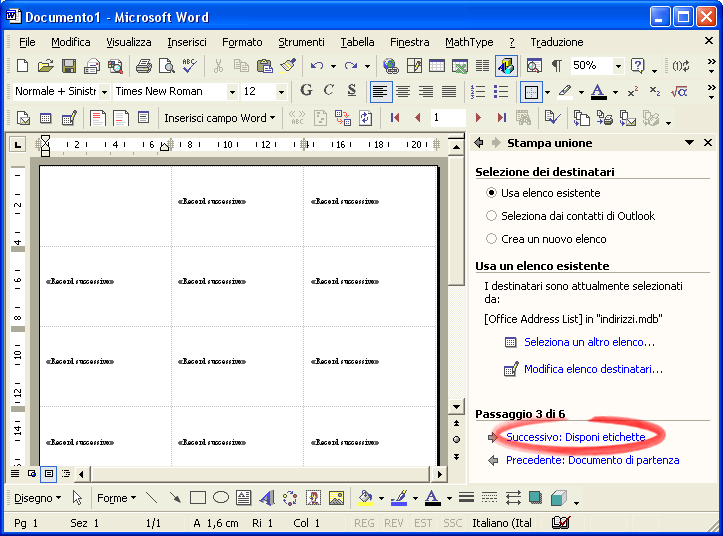
Passo 4. Fai clic su Blocco di indirizzi…
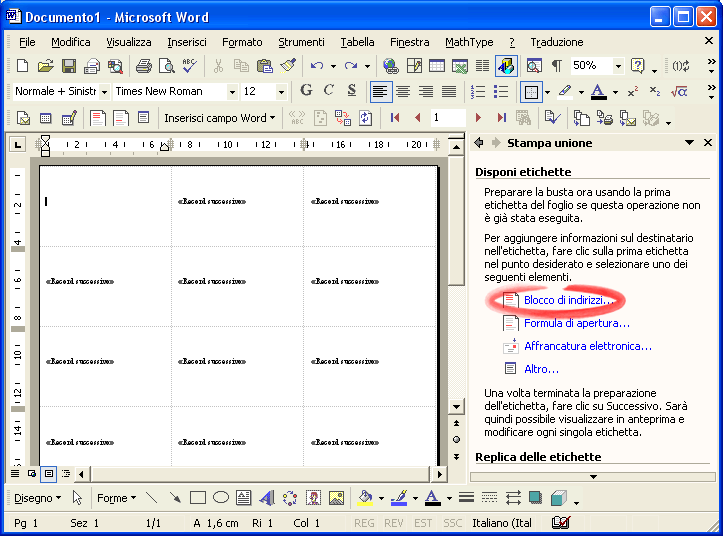
Scegli il modo in cui vuoi che venga scritto l’indirizzo: nel riquadro Anteprima puoi vedere come verrà scritto.
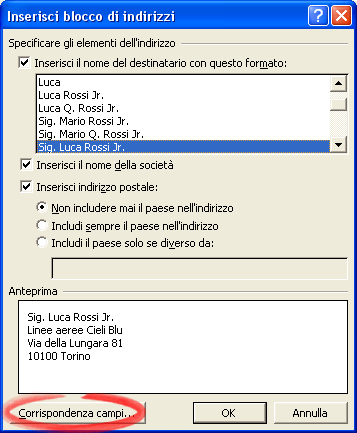
Prima di premere OK, premi il bottone Corrispondenza Campi . Sicuramente c’è da correggere almeno il campo Indirizzo 1 .
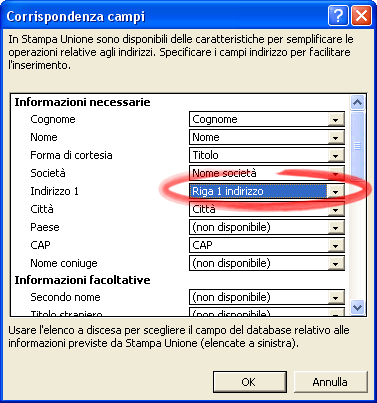
Premi OK su entrambi le finestre. Riapparirà il foglio con le etichette. Nella prima comparirà ««AddressBlock»» . Premi il tasto Aggiorna tutte le etichette .
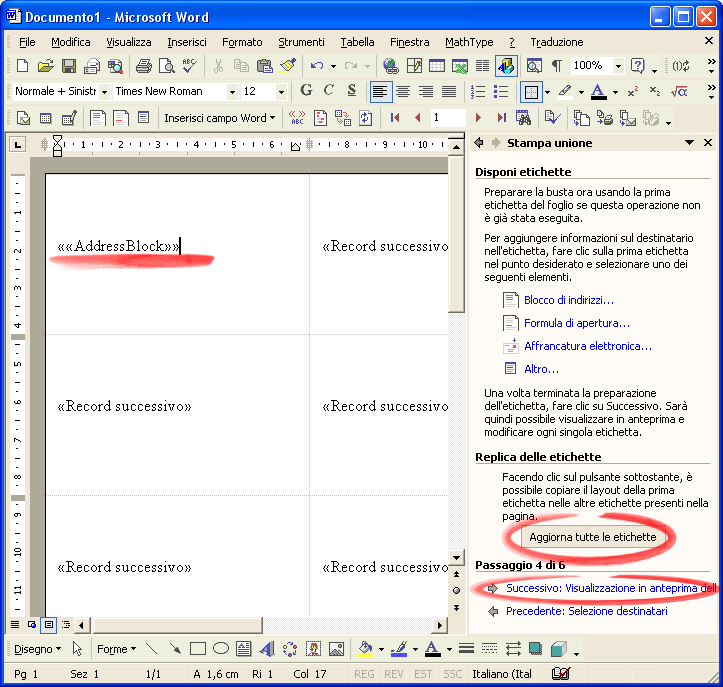
Passo 5. Infine fai clic su Successivo: Visualizzazione in anteprima delle etichette . Il risultato è il seguente
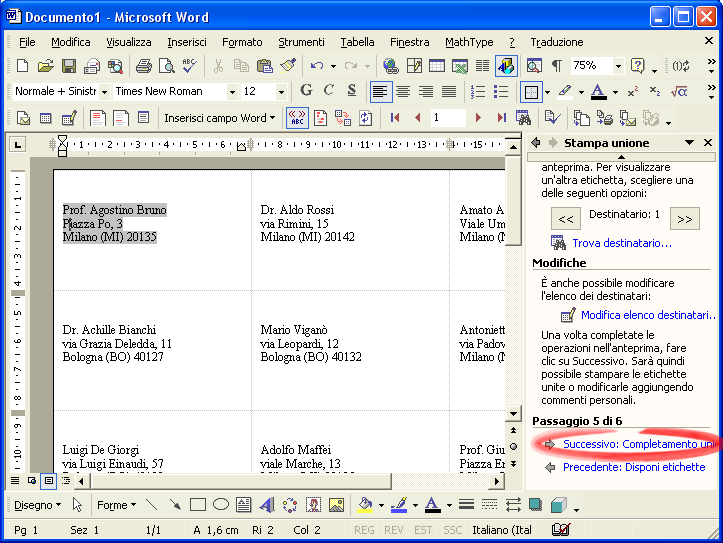
Fai clic su Successivo: Completamento unione .
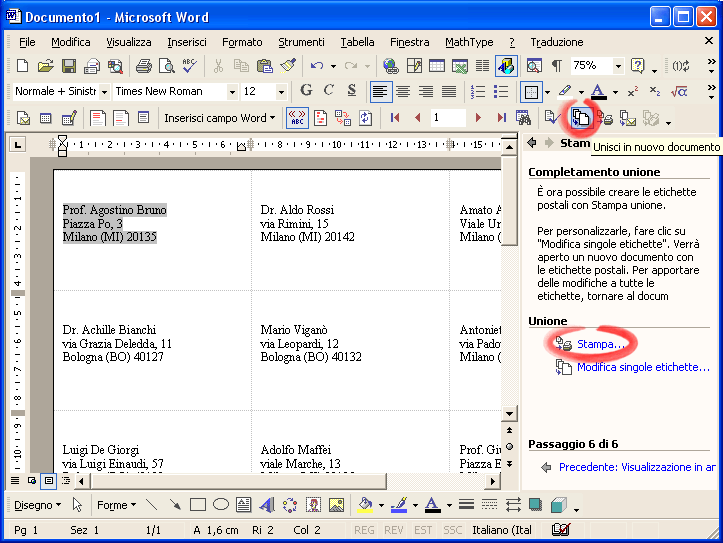
Fai clic su Stampa… per stampare le etichette, o sul bottone Unisci in nuovo documento per salvare il file ottenuto in modo da riutilizzarlo.
Quando sei diventato esperto puoi fare a meno della procedura guidata. Dalla voce di menu Strumenti seleziona Lettere e indirizzi / Mostra barra degli strumenti unione. Compare una barra degli strumenti che ti permette di percorrere tutta la sequenza appena vista, facendo clic sui vari bottoni da sinistra verso destra.

 Impostazioni documento principale
Impostazioni documento principale
 Apri origine dei dati
Apri origine dei dati
 Seleziona i destinatari della stampa unione
Seleziona i destinatari della stampa unione
 Inserisci blocco di indirizzi
Inserisci blocco di indirizzi
 Visualizza i dati uniti
Visualizza i dati uniti
 Verifica la corrispondenza dei campi
Verifica la corrispondenza dei campi
 Unisci in un nuovo documento
Unisci in un nuovo documento
 Unisci alla stampante
Unisci alla stampante
Antonio Bernardo
Creare un curriculum con Word
|
Creare un curriculum con Word Word possiede diversi tipi già impostati di curriculum. Dalla barra dei menu seleziona File , Nuovo , in Word XP Modelli generali . Scegli la scheda Altri documenti , quindi scegli il tipo di curriculum.
Vediamo però un altro esempio di curriculum, partendo da un documento vuoto. Scrivi Curriculum vitae di Nome COGNOME , scegli come tipo di carattere Thaoma 12 e Thaoma 20
Posizionati sul rigo seguente e dalla barra dei menu seleziona Tabella / Inserisci / Tabella
Imposta una tabella con 2 colonne e 6 righe, tante righe quante sono le sezioni del tuo curriculum. Porta a 3 cm il delimitatore tra le due celle, trascinandolo con il mouse.
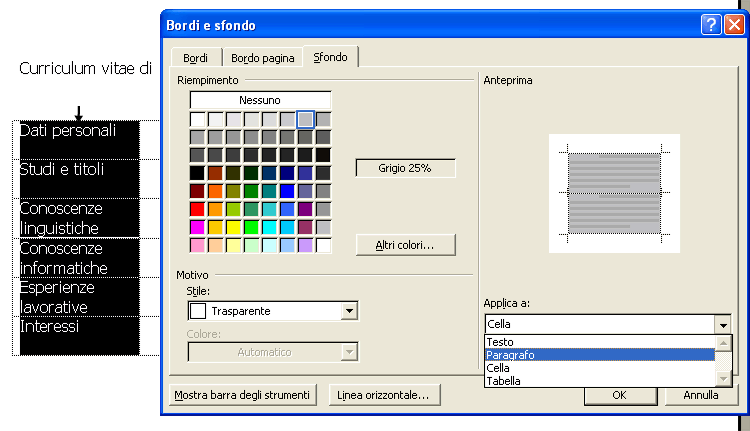
Per rendere più eleganti i bordi della tabella, posiziona il cursore all’interno della tabella e fai clic con il tasto destro del mouse. Dal menu contestuale scegli Bordi e sfondo …
Dalla finestra Bordi e sfondo scegli Predefiniti: Tutti Stile: punteggiato Colore: grigio chiaro
Nella colonna sinistra scrivi il titolo delle sezioni, uno per cella.
E’ giunto il momento di cominciare a salvare il documento. Dalla barra dei menu seleziona in sequenza File / Salva con nome . Scegli la cartella e dai un nome opportuno al file. Consiglio di chiamarlo curriculum030608.doc per tenere traccia anche della data annomesegiorno in cui è stato creato il curricumulum. In seguito, man mano che si aggiunge una parte significativa di testo salvare premendo semplicemente il pulsante salva Seleziona la prima colonna e dalla barra dei menu seleziona in sequenza Formato / Bordi e sfondo.. .
Scegli la scheda Sfondo e imposta i seguenti parametri Riempimento: Grigio 25% Applica a: Paragrafo A questo punto compilare la colonna di destra con i propri dati. Per una serie di titoli o esperienze suddivisi per anni impostare i margini del righello come in figura.
Scarica l’esempio (word 29 KB)
Bernardo
|
I premi per MatematiCup

| Piazzamento | Premi |
| 1a squadra classificata | Coppa+medaglie+libri |
| 2a squadra classificata | Coppa+medaglie+libri |
| 3a squadra classificata | Coppa+medaglie+libri |
| 1a squadra femminile | Coppa+medaglie+libri |
| 1a scuola classificata | Targa+libri |
| Ulteriori riconoscimenti, non cumulabili con i precedenti, saranno assegnati a | |
| migliore gruppo di prima classe | Coppa |
| migliore gruppo classe seconda | Coppa |
| migliore gruppo classe terza | Coppa |
| migliore squadra in aritmetica e algebra | Coppa |
| migliore squadra in geometria | Coppa |
| migliore squadra in logica | Coppa |
| migliore squadra in statistica e probabilità | Coppa |
| migliore squadra negli allenamenti | Coppa + medaglie |
Tutte le scuole delle squadre premiate riceveranno un abbonamento semestrale gratuito al servizio di filtro Internet a protezione dei minori fornito da KBIT srl.
Su richiesta del docente saranno rilasciati attestati per ogni studente iscritto.
Come si partecipa
Le modalità di partecipazione è la seguente:

Ogni scuola secondaria di primo grado può iscrivere una o più squadre; ogni squadra comprende da 12 (min.) a 30 (max.) alunni ciascuna e un allenatore-insegnate.
La squadra è suddivisa in tre gruppi, un gruppo di classe prima, uno di seconda e uno di terza; ognuno dei tre gruppi deve avere un struttura organizzata con compiti specifici: un capitano che organizza il lavoro del gruppo, un operatore al computer che è responsabile dell’inserimento delle risposte e i collaboratori che concorrono, assieme al capitano e all’operatore al computer, alla risoluzione dei quesiti.
I tre gruppi sono coordinati e allenati da un professore che fa da docente referente per la squadra.
Lle scuole che partecipano con più squadre sono sollecitate a formare anche squadre di sole ragazze: è previsto, infatti, un riconoscimento per la migliore squadra tutta femminile.
Oni squadra deve avere a disposizione un’aula, o un laboratorio, che nel giorno della gara sarà riservato esclusivamente alla competizione; è opportuno che ogni squadra abbia a disposizione tre computer connessi contemporaneamente a Internet, uno per ogni gruppo, è comunque possibile partecipare anche con un solo computer connesso a Internet per squadra.
L’iscrizione può essere effettuata esclusivamente dal docente referente (l’allenatore della squadra) e avviene esclusivamente compilando un apposito modulo on-line; non sono previste spese di partecipazione né per la scuola né per gli studenti. Al momento dell’iscrizione il docente referente e il dirigente scolastico ricevono un gruppo di 5 password, una per modificare i dati di iscrizione, una per gli allenamenti e una per ogni gruppo classe. La password per gli allenamenti può essere comunicata a ogni studente della squadra, in modo che ciascuno possa allenarsi anche da casa, con i propri amici e la propria famiglia. Le password per la gara siano custodite dal docente-allenatore e restino segrete fino al giorno della gara.
L’allenatore aiuta gli alunni nelle fasi di organizzazione, iscrizione e allenamento della squadra.
Gli allenamenti possono essere fatti in qualsiasi momento sia a scuola sia fuori dalla scuola. I quesiti sono analoghi a quelli della gara e i punteggi sono calcolati allo stesso modo.
La gara si svolge in un’unica sessione dalle 9.00 alle 12.30 del giorno 7 maggio 2008. Dalle 9.00 alle 9.30 i concorrenti prendono posto suddivisi in tre gruppi, ciascuno davanti al proprio computer di gara e ciascuno con il proprio ruolo (capitano, operatore, risolutore). L’operatore inserisce il nome della squadra e la password di gara del proprio gruppo. A partire dalle 9.30 tutte le squadre iscritte avranno accesso ai quesiti. Su ciascun computer compaiono soltanto i quiz che devono essere risolti dal gruppo che lavora con quel computer.
Il docente allenatore durante la gara partecipa rimuovendo eventuali problemi di connessione o di malfunzionamento dei computer. Il docente è responsabile della valenza didattica dell’iniziativa, sia nei confronti dei propri studenti sia nei confronti degli organizzatori della gara e scoraggerà eventuali comportamenti antisportivi dei propri allievi. Durante la gara, l’allenatore può connettersi su un altro computer non utilizzato per la gara per visualizzare in tempo reale la classifica generale e incoraggiare la propria squadra ad ottenere la prestazione massima.
Ogni studente durante lo svolgimento della gara collabora con il proprio gruppo per cercare di risolvere correttamente nel minor tempo possibile il maggior numero di quiz. Può utilizzare, calcolatrici, software, libri e quant’altro ritiene necessario; non può comunicare né a voce, né al telefono, né in chat, né per e-mail con persone che non fanno parte della propria squadra, non può chiedere aiuto al proprio allenatore per la risoluzione degli esercizi.
Genitori, parenti, amici e conoscenti possono connettersi via Internet alla pagina dei punteggi che sarà aggiornata in tempo reale e assistere allo svolgimento della gara.
La valutazione dei quesiti è effettuata sia in base al livello di difficoltà del quesito sia in base al tempo impiegato per risolverlo. Per ciascun quiz viene indicato il livello di difficoltà, da 1 a 5, espresso graficamente in stelline. Da quando il quiz viene aperto ci sono 2 minuti di tempo per leggerlo con attenzione e discuterlo con i compagni di squadra, in questo lasso di tempo il computer non accetta risposte. Ciò obbliga gli studenti a leggere con cura il testo e di discutere con i compagni prima di rispondere. Dopo i 2 minuti di lettura e condivisione del quiz, parte un cronometro che si ferma quando l’addetto al computer inserisce e conferma la risposta in maniera definitiva. Il tempo di risoluzione dell’esercizio e quindi il punteggio ottenuto non dipende dalla velocità di connessione del computer (chi ha una connessione ISDN non è svantaggiato rispetto a chi ha una connessione ADSL) ma esclusivamente dal tempo intercorso tra quando il computer della squadra ha ricevuto il quesito e quando l’operatore ha premuto il bottone di conferma della soluzione. Il punteggio per ciascun quiz parte dal livello di difficoltà del quesito (numero di stelline) e diminuisce con il trascorrere del tempo fino alla conferma della risposta. Il punteggio della squadra è dato dalla somma dei punteggi dei quiz risolti da ogni gruppo. La classifica viene elaborata contemporaneamente alla prova e può essere visualizzata in qualsiasi momento della gara. Per evitare distrazioni è preferibile che la classifica sia visualizzata soltanto dall’allenatore e su un altro computer.
La proclamazione dei vincitori avviene alcuni giorni dopo lo svolgimento della gara. Per tutte le squadre che si qualificano ai primi posti, la giuria accerta che l’iscrizione e lo svolgimento della gara sia stata conforme alle regole.
Il gruppo di lavoro
Gruppo promotore: Antonio Bernardo (Matematicamente.it), Mario Bochicchio (DIDA-Lab), Massimo Mazzitelli (Kataweb), Domenico Lenzi (Mathesis)
Comitato tecnico scientifico: Antonio Bernardo, Mario Bochicchio, Domenico Lenzi, Andrea La Forgia (Mathesis nazionale), Laura Todisco (matematicamente.it).
Redattori dei quesiti: Antonio Bernardo, Laura Todisco, Domenico Lenzi.
Revisori dei quesiti: Luca Barletta, Antonio Bernardo, Flavio Cimolin, Luca Lussardi, Luciano Sarra, Laura Todisco, Paolo Giovanni Zanin
Illustratore: Squaz (Pasquale Todisco)
Direzione sviluppo software: Federico Zanchetta (Kataweb)
Il gruppo di lavoro è in fase di costituzione ed è aperto a docenti che volessero farne parte. Scrivere a [email protected]
Lettera agli studenti
Caro studente,
probabilmente conosci già la storiella dello scienziato che vuole misurare quanto è intelligente uno scimpanzé. Lo scienziato ha appeso al soffitto una banana e sul pavimento ha messo alcune scatole: si aspetta che lo scimpanzé userà le scatole per formare una scala e raggiungere la banana. La scimmia, da parte sua, osserva stupita il comportamento dello scienziato: perché appendere al soffitto una banana quando è già pronta per essere mangiata? Tuttavia aspetta paziente e quando lo scienziato passa proprio sotto la banana, fa un salto, gli sale sulle spalle e prende al volo la banana.
Molte volte noi insegnanti disponiamo una serie di formulette che dovrebbero aiutarti a risolvere un problema ma i problemi reali non sempre hanno soluzioni previste in anticipo. Quasi sempre occorre invenzione, intelligenza pronta, coraggio e spirito di iniziativa per spiccare un salto quando c'è bisogno e prendere al volo la soluzione del problema.
La gara che stai per affrontare non è un test su quanta matematica conosci ma è un gioco, una sfida con altri tuoi coetanei, un gioco di squadra. Per vincere devi risolvere il maggior numero di quiz nel più breve tempo possibile. Per ottenere un buon risultato devi allenarti, seguire i consigli del tuo allenatore e soprattutto imparare a collaborare con i tuoi compagni di squadra. Come dice un grande maestro, George Polya, risolvere problemi è un'arte pratica, come il nuotare o lo sciare o il suonare il piano: se desideri imparare a nuotare, devi gettarti in acqua e se desideri diventare un risolutore di problemi, devi risolvere problemi.
Allora trova la tua squadra e il tuo allenatore, ci sono tanti ragazzi che sono pronti per la sfida.
Lettera ai docenti e caratteristiche didattiche della gara
Caro collega,
tantissimi documenti ed esperienze ci confermano che l’insegnamento della matematica è efficace quando è accompagnato da una sfida tra l’allievo e un quesito ben formulato che lo attrae. L’allievo ha la sensazione che sia facile, alla sua portata, che lo risolverà in un lampo e senza accorgersene si addentra nei meandri del pensiero, del ragionamento, del calcolo, della rappresentazione grafica … e scoprirà di aver fatto matematica.
Già 4000 anni fa, come risulta dal Papiro di Rhind, in Egitto la matematica si insegnava per problemi. Problemi dalla formulazione semplice, che fanno riferimento a oggetti della vita comune, che attraggono e incuriosiscono. Uno di questi recita "Ci sono sette case, in ogni casa ci sono sette gatti, ogni gatto mangia sette topi, ogni topo mangia sette spighe, ogni spiga produce sette hekath di grano, quanti sono in tutto?" Chi non ha mai sentito questo indovinello? Magari raccontato con personaggi diversi. Tenendo conto che il papiro su cui è trascritto è stato ritrovato soltanto 150 anni fa, si può ritenere che questo problema ha attraversato quattro millenni, duranti i quali l’umanità lo ha tramandato oralmente o lo ha riscoperto più volte. Il metodo di insegnamento che il problema si porta dietro ha superato la diversità delle culture, dei mezzi di comunicazione, degli strumenti di scrittura, del simbolismo matematico e proprio per questo rimane un punto di riferimento per chi vuole insegnare la matematica.
Per citare un altro caso storico, ricordo il libretto di Alcuino di York, ora tradotto anche in italiano, Problemi per rendere acuta la mente dei giovani, Edizioni ETS. Alcuino di York era un monaco inglese che nel 781 venne chiamato alla corte di Carlomagno per istruire i giovani nobili. In quel periodo raccolse una serie di problemi divertenti e stimolanti la cui origine si perde nella notte dei tempi. Uno di questi recita: "Un uomo doveva trasportare aldilà di un fiume un lupo, una capra e un cavolo e non poté trovare altra barca se non una che era in grado di portare soltanto due di essi. Gli era stato ordinato però di trasportare tutte queste cose di là senza alcun danno. Chi è in grado dica in che modo poté trasferirli indenni". Chissà quante volte ti hanno proposto o hai proposto questo quesito. L’espressione "salvare capra e cavoli" deriva sicuramente da questo antichissimo quesito, ormai sedimentato nella nostra cultura e tramandato di generazione in generazione. Il monaco Alcuino aveva visto in questo metodo ‘popolare’ di insegnare la via per introdurre i giovani allo studio della matematica.
Un ultimo caso storico che voglio ricordare è la gara di matematica a squadre del 1223 a Pisa, alla presenza dell’imperatore Federico II di Svevia. Uno dei quesiti della gara era il seguente: "Un tale chiude una coppia di conigli tra quattro mura. Quante coppie potranno essere generate in un anno, supponendo che ogni mese ognuna delle coppie genera una nuova coppia che comincia a procreare dal secondo mese di vita?". La gara fu vinta da Fibonacci, il quale rispose in maniera così rapida che molti pensarono a un imbroglio. Da questo quesito sono venuti fuori i famosi numeri di Fibonacci che occupano un posto di rilievo nella matematica.
In un momento in cui tutti lamentiamo uno scarso interesse dei giovani verso la matematica questi significativi momenti storici ci indicano la soluzione: ripercorrere le vie di questi grandi maestri del passato e recuperare la tradizione delle dispute matematiche per fare apprezzare ai giovani di oggi il piacere del pensare corretto. Quale migliore occasione allora per unire la tradizione delle sfide di matematica con l’innovazione tecnologica di Internet.
Obiettivo primario di MatematiCup è quello di recuperare l’interesse dei giovani nei confronti della matematica e di rafforzare le competenze matematiche che rispondono alle esigenze di vita dei ragazzi in quanto persone che esercitano nella società un ruolo costruttivo, basato sulla riflessione.
La gara on line “MatematiCup” si propone inoltre di sperimentare modalità di partecipazione in rete alle gara di matematica: da un lato per risolvere i problemi logistici di spostamento dei ragazzi, che è il problema principale delle gare in presenza, dall’altra per diffondere l’uso delle nuove tecnologie e in particolare le modalità collaborative e partecipative di Internet.
MatematiCup si caratterizza per
L’apprendimento collaborativo mediato da Internet. L’insegnamento oggi non può più restare confinato all’interazione tra studenti e docenti nelle aule scolastiche. Gli strumenti tecnologici permettono una interazione tra gruppi di persone che può rendere l’insegnamento un’esperienza più ampia. Inoltre, l’uso di Internet se guidato da un lato dagli insegnanti della classe e dall’altro da organizzazioni scientifico-culturali (università, associazioni di insegnanti, testate giornalistiche qualificate) permette di rendere l’apprendimento attraverso Internet non un apprendimento accidentale e casuale ma guidato e finalizzato.
L’iscrizione aperta. L’iscrizione alla gara è completamente gratuita e permette a ciascuna scuola di iscrivere un qualsiasi numero di studenti. Questo rende MatematiCup un’esperienza libera di impressioni negative sulla lucrosità delle azioni culturali e soprattutto permette alle scuole e ai docenti di coinvolgere non solo gli studenti riconosciuti bravi in matematica ma tutti quelli che hanno piacere a confrontarsi e a sforzarsi di incontrare questa disciplina. La finalità non è quella di selezionare gli studenti già bravi ma diffondere il piacere di fare matematica.
Il gruppo classe. La gara “MatematiCup” si propone come un’esperienza di confronto e di gruppo, in quanto è esplicitamente richiesto che i ragazzi si confrontino prima di rispondere alle domande. Inoltre l’aver messo insieme in un’unica squadra studenti di prima, seconda e terza classe permette di realizzare una forma di apprendimento collaborativo tra pari (studenti delle classi superiori verso studenti delle classi inferiori) che difficilmente si riesce a realizzare nella usuale attività didattica. E’ noto invece che questo tipo di apprendimento è particolarmente efficace.
I quesiti oggetto della gara. MatematiCup si caratterizza per l’accento che mette sulle applicazioni della matematica nella vita quotidiana. Ogni quesito infatti viene inserito in un contesto reale, che può andare dall’ambito personale e strettamente vicino all’esperienza di vita dei ragazzi di 12-14 anni ad ambiti tecnico-scientifici. Più precisamente, gli ambiti sono: personale, familiare, scolastico, sportivo, lavorativo, economico e tecnico-scientifico. I quesiti sono stati suddivisi sia per classi scolastiche (I classe, II classe, II classe) sia per temi (numeri e relazioni, forme e misure, dati e previsioni, logica e teoria elementare degli insiemi). L’orientamento è stato quello di seguire l’impostazione dei quesiti dell’indagine internazionale OCSE-PISA.
La valutazione dei quesiti. Le risposte ai quesiti sono sempre numeri intere o lettere in modo da consentire la valutazione automatica delle risposte. La possibilità di vedere in tempo reale la classifica complessiva della gara e le singole classifiche per categorie rende la competizione particolarmente interattiva e partecipativa.
Attività integrative, laboratoriali, interdisciplinari. MatematiCup può colmare una lacuna di contenuti per le attività di laboratorio, attività integrative e interdisciplinari. Per queste attività, infatti, l’insegnante non ha molte proposte che provengano dai libri di testo o da altri materiali a sua disposizione. Inoltre l’informatica (e Internet) non è proposta come esperienza fine a se stessa ma come strumento di mediazione di contenuti disciplinari.
L’attenzione alla scuola di livello inferiore. Attualmente l’uso delle tecnologie e le esperienze formative con tecnologie avanzate sembra riguardare esclusivamente la scuola superiore di secondo grado. Tutte le scuole superiori di secondo grado sono ormai dotate di diversi laboratori di informatica, connessioni a Internet e altro, la scuola secondaria di primo grado è rimasta spesso fuori dai grossi finanziamenti per l’adeguamento tecnologico delle scuole. La cura dei laboratori e le connessioni a Internet sono spesso lasciate a pochi volontari. Questa gara può servire per tenere aggiornati e funzionanti i laboratori e le connessioni a Internet, spingere a cercare di colmare il gap tecnologico con le scuole superiori.
L’attenzione alle problematiche di genere. Senza entrare in problematiche complesse legate alle disparità di genere, MatematicCup si propone di contribuire a spingere le ragazze a confrontarsi con la matematica e a superare l’idea sociale di fondo per la quale le ragazze sono poco inclini agli studi scientifici.
La possibilità di non spostare i ragazzi. Dal punto di vista logistico MatematiCup permette di evitare complessità logistiche e burocratiche legate allo spostamento dei ragazzi minorenni. Solitamente le gare di matematica vengo svolte in maniera selettiva all’interno della stessa scuola, i ragazzi ‘migliori’ partecipano alle selezioni a livello provinciale, poi regionale, infine nazionale. Ciò comporta un’organizzazione complessa per spostare gli alunni e rende comunque l’esperienza della gara un’esperienza di pochi.
L’orientamento. La gara condotta con una modalità libera e aperta a tutti permette agli studenti di orientarsi nella scelta della scuola di secondo grado in base alla propria passione e/o capacità per la matematica.
Ti invitiamo a mettere la maglia di allenatore e formare la squadra vincente della tua scuola.
Terzo incontro Matematicamente
 A Roma tra il 20 e il 21 ottobre 2007 si è tenuto il terzo incontro della comunity di Matematicamente.it. Hanno partecipato da tutta Italia e di tutte le fasce d'età undici tra i membri più attivi.
A Roma tra il 20 e il 21 ottobre 2007 si è tenuto il terzo incontro della comunity di Matematicamente.it. Hanno partecipato da tutta Italia e di tutte le fasce d'età undici tra i membri più attivi.
-Paola, vulcanica promotrice e organizzatrice del Meeting – Roma 2007
-Il giovane cicerone Steven, attento selezionatore delle bellezze (artistiche sic!) romane
-Antonio-Admin a sorpresa ha superato montagne e fiumi per raggiungere il meeting
-Luca, presente a tutti i raduni
-Cheguevilla, arrivato a cavallo del suo 'mulo'
-Fireball, che finalmente abbiamo conosciuto
-Kroldar, possibile organizzatore del prossimo meeting
-Giacomo e Vessa, che si sono appassionati al Colosseo
-Thomas, da bravo fisico si è cimentato con successo con il sistema idraulico del BB che ha ospitato il gruppo
-Eredir, matricola di questi incontri, che speriamo di rivedere e di risentire
-Camillo, che ha battuto tutti in quanto a vitalità e desiderio di restare ragazzo (essendo l'autore di queste descrizioni compare per ultimo)
I meeting precedenti erano stati tenuti a Milano e Firenze. Quest'anno la scelta è andata su Roma. Anche i matematici hanno bisogno di vedere un po' di storia: il Colosseo, l'Altare della Patria, qualche Chiesa lungo il tragitto, fori imperiali e Campidoglio.
Un po' di chiacchere qua e là e poi come al solito le migliori discussioni si fanno davanti a un piatto di spaghetti e qualche pezzo di torta. Abbiamo discusso sull'andamento del forum attuale, politica amministrativa, gestione e creazione di nuove sezioni, gestione di utenti problematici. Infine Admin ha propagandato un po' di sviluppi futuri: il progetto Matematicamente.it non finisce mica qui! Siamo ancora all'inizio. A qualcuno non è dispiaciuto cogliere l'occasione per un po' di discussioni tecniche, modelli interessanti di cui si stanno occupando professionalmente alcuni di noi. Qualche consiglio poi dei 'più vecchi' per dare qualche dritta ai più giovani sul futuro universitario che li attende.

La didattica della matematica nella scuola elementare – Corso on line
 Riceviamo e pubblichiamo. ALTRASCUOLA organizza un corso sulla didattica della matematica nella scuola elementare. Il corso propone agli insegnanti una traccia didattica per guidare alla costruzione dei concetti delle operazioni legandoli a situazioni problematiche. Il corso dura cinque settimane e prevede la lettura di materiali, la realizzazione di esercitazione e la partecipazione al forum e alla chat di classe. Data inizio:12 novembre 2007 – Durata: 5 settimane – Termine iscrizioni: 9 novembre 2007.
Riceviamo e pubblichiamo. ALTRASCUOLA organizza un corso sulla didattica della matematica nella scuola elementare. Il corso propone agli insegnanti una traccia didattica per guidare alla costruzione dei concetti delle operazioni legandoli a situazioni problematiche. Il corso dura cinque settimane e prevede la lettura di materiali, la realizzazione di esercitazione e la partecipazione al forum e alla chat di classe. Data inizio:12 novembre 2007 – Durata: 5 settimane – Termine iscrizioni: 9 novembre 2007.
http://corsi.altrascuola.it/modules.php?name=Sections&sop=viewarticle&artid=204
Riceviamo e pubblichiamo la seguente notizia
Corso: La didattica della matematica nella scuola elementare
Obiettivi: Il corso propone agli insegnanti una traccia didattica per guidare alla costruzione dei concetti delle operazioni legandoli a situazioni problemiche. Il percorso si avvale di due modelli di rappresentazioni grafiche. Si propone fare esperienze di manipolazione con gli oggetti che costruiscano situazioni additive e moltiplicative. Da queste si passa alla loro rappresentazione grafica con i due modelli grafici. Attraverso passaggi graduati si costruiscono i concetti delle operazioni. I modelli grafici evidenziano: il ruolo logico delle parole-problema, permettendo la costruzione di situazioni problemiche senza l'uso dei numeri. Inoltre essi evidenziano le relazioni quantitative tra i numeri stessi. Il passaggio dal grafico alle operazioni con i relativi simboli avviene in modo graduale, in modo da poter essere adattato alle esigenze della singola classe. Il corso dura cinque settimane e prevede la lettura di materiali, la
realizzazione di esercitazione e la partecipazione al forum e alla chat di classe. Giorni e orari per le chat verranno comunicati dal tutor.
Data inizio:12 novembre 2007
Durata: 5 settimane
Costo: 144 €
Data termine iscrizioni: 9 novembre 2007
Per poter partecipare al corso bisogna avere a disposizione un PC con accesso ad Internet, la disponibilità ad effettuare le esercitazioni, a contribuire alle discussioni e a partecipare alle sezioni di chat.
Link alla scheda del corso:
http://corsi.altrascuola.it/modules.php?name=Sections&sop=viewarticle&artid=204
Per informazioni: [email protected]
Limiti notevoli
In questi appunti di analisi matematica per l’università si dà un tabella dei limiti notevoli
2007 – liceo scientifico – scuole italiane all’estero – calendario australe
 Il tema di matematica svolto per l’esame di stato per il liceo scientifico nelle scuole italiane all’estero, secondo il calendario australe.
Il tema di matematica svolto per l’esame di stato per il liceo scientifico nelle scuole italiane all’estero, secondo il calendario australe.
51. Editoriale
Scacchi su matematicamente: sfida un amico
 Abbiamo attivato il gioco degli scacchi, da giocare in coppia con amici (… e perché no, anche con nemici). Per giocare occorre registrasi al sito ed avere nome utente e password. Nella sezione dedicata agli scacchi cercate in "Nuova partita" qualcuno da sfidare o accettate la sfida di qualcuno che vuole giocare. Giocare è piuttosto semplice … correggo muovere i pezzi è piuttosto facile, vincere è tutt'altra cosa.
Abbiamo attivato il gioco degli scacchi, da giocare in coppia con amici (… e perché no, anche con nemici). Per giocare occorre registrasi al sito ed avere nome utente e password. Nella sezione dedicata agli scacchi cercate in "Nuova partita" qualcuno da sfidare o accettate la sfida di qualcuno che vuole giocare. Giocare è piuttosto semplice … correggo muovere i pezzi è piuttosto facile, vincere è tutt'altra cosa.
52. Metallica 3: Io buffo e i quadri alla parete
 Ho fatto le scale quattro a quattro, la campanella della prima ora era già suonata da un pezzo e non si vedeva più nessuno in giro. Sono sbarcato sul pianerottolo tutto sudato e col fiatone. Alzo gli occhi e chi vedo? Vedo lei che mi viene incontro lungo il corridoio, facendo il solito sorriso di quando scopre una cosa buffa. Accidenti a quell’imbranata di mia sorella che ha sbagliato a mettere la sveglia!
Ho fatto le scale quattro a quattro, la campanella della prima ora era già suonata da un pezzo e non si vedeva più nessuno in giro. Sono sbarcato sul pianerottolo tutto sudato e col fiatone. Alzo gli occhi e chi vedo? Vedo lei che mi viene incontro lungo il corridoio, facendo il solito sorriso di quando scopre una cosa buffa. Accidenti a quell’imbranata di mia sorella che ha sbagliato a mettere la sveglia!
Questo è il terzo di sei racconti dedicati al calcolo combinatorio. I racconti possono essere utilizzati dagli studenti che vogliono imparare la base di questo tipo di calcolo o da insegnanti che vogliono provare qualche idea diversa per insegnarlo.
53. Il teorema dei quattro colori e la teoria dei grafi
 In questo articolo dopo aver introdotto il Teorema dei quattro colori si spiega come esso possa essere formulato in termini di teoria dei grafi. Si raccontano poi i vari contributi che hanno portato alla dimostrazione definitiva del teorema, sottolineando come la dimostrazione finale sia stata possibile grazie ai risultati parziali e alle dimostrazione errate di vari matematici.
In questo articolo dopo aver introdotto il Teorema dei quattro colori si spiega come esso possa essere formulato in termini di teoria dei grafi. Si raccontano poi i vari contributi che hanno portato alla dimostrazione definitiva del teorema, sottolineando come la dimostrazione finale sia stata possibile grazie ai risultati parziali e alle dimostrazione errate di vari matematici.
Crucinumero: Quincentocinquantacinque
54. Metodi infinitesimali nell’antichità. Prima parte
 L’infinito negli antichi e il metodo di esaustione. Sebbene il calcolo infintesimale abbia ufficialmente inizio nel XVII secolo per opere indipendenti di Newton e Leibniz, anche nell’antichità si trovano metodi che possono essere definiti di natura infinitesimale
L’infinito negli antichi e il metodo di esaustione. Sebbene il calcolo infintesimale abbia ufficialmente inizio nel XVII secolo per opere indipendenti di Newton e Leibniz, anche nell’antichità si trovano metodi che possono essere definiti di natura infinitesimale
Sudoku 004 – Livello molto facile
sudoku molto facile per solutori principianti
Regolamento
/
/C/o/m/p/e/t/i/z/i/o/n/e/ /n/a/z/i/o/n/a/l/e/ /d/i/ /m/a/t/e/m/a/t/i/c/a/ /a/ /s/q/u/a/d/r/e/ /s/u/ /I/n/t/e/r/n/e/t//p/e/r/ /s/c/u/o/l/e/ /s/e/c/o/n/d/a/r/i/e/ /d/i/ /p/r/i/m/o/ /g/r/a/d/o///M/A/T/E/M/A/T/I/C/U/P///I/I/ /e/d/i/z/i/o/n/e/ /a/./s/./ /2/0/0/7///2/0/0/8///&/n/b/s/p/;////R/E/G/O/L/E/ /E/ /M/O/D/A/L/I/T/&/A/g/r/a/v/e/;/ /D/I/ /S/V/O/L/G/I/M/E/N/T/O/ /D/E/L/L/A/ /G/A/R/A/////&/b/u/l/l/;/&/n/b/s/p/;//O/g/n/i/ /s/c/u/o/l/a// /s/e/c/o/n/d/a/r/i/a/ /d/i/ /p/r/i/m/o/ /g/r/a/d/o/ /p/u/&/o/g/r/a/v/e/;/ /i/s/c/r/i/v/e/r/e/ /u/n/a/ /o/ /p/i/&/u/g/r/a/v/e/;/ /s/q/u/a/d/r/e/,/ /c/i/a/s/c/u/n/a/ /s/u/d/d/i/v/i/s/a/ /i/n/ /t/r/e/ /g/r/u/p/p/i/,/ /u/n/ /g/r/u/p/p/o/ /d/i/ /c/l/a/s/s/e/ /p/r/i/m/a/,/ /u/n/o/ /d/i/ /s/e/c/o/n/d/a/ /e/ /u/n/o/ /d/i/ /t/e/r/z/a/,/ /c/o/m/p/l/e/s/s/i/v/a/m/e/n/t/e/ /d/a/ /u/n/ /m/i/n/i/m/o/ /d/i/ /1/2/ /a/ /u/n/ /m/a/s/s/i/m/o/ /d/i/ /3/0/ /a/l/u/n/n/i/./ /I/ /t/r/e/ /g/r/u/p/p/i/ /s/o/n/o/ /c/o/o/r/d/i/n/a/t/i/ /e/ /a/l/l/e/n/a/t/i/ /d/a/ /u/n/ /p/r/o/f/e/s/s/o/r/e/ /c/h/e/ /f/a/ /d/a/ /d/o/c/e/n/t/e/ /r/e/f/e/r/e/n/t/e/ /p/e/r/ /l/a/ /s/q/u/a/d/r/a/./ /O/g/n/i/ /g/r/u/p/p/o/ /d/i/ /s/t/u/d/e/n/t/i/ /a/v/r/&/a/g/r/a/v/e/;/ /u/n/ //c/a/p/i/t/a/n/o// /c/h/e/ /o/r/g/a/n/i/z/z/a/ /i/l/ /l/a/v/o/r/o/ /d/e/l/ /g/r/u/p/p/o/,/ /u/n/ //o/p/e/r/a/t/o/r/e// /a/l/ /c/o/m/p/u/t/e/r/ /c/h/e/ /&/e/g/r/a/v/e/;/ /r/e/s/p/o/n/s/a/b/i/l/e/ /d/e/l/l/&/#/3/9/;/i/n/s/e/r/i/m/e/n/t/o/ /d/e/l/l/e/ /r/i/s/p/o/s/t/e/ /a/t/t/r/a/v/e/r/s/o/ /i/l/ /c/o/m/p/u/t/e/r/,/ /i/ //c/o/l/l/a/b/o/r/a/t/o/r/i// /c/h/e/ /c/o/n/c/o/r/r/o/n/o/,/ /a/s/s/i/e/m/e/ /a/l/ //c/a/p/i/t/a/n/o// /e/ /a/l/l/&/#/3/9/;//o/p/e/r/a/t/o/r/e//,/ /a/l/l/a/ /r/i/s/o/l/u/z/i/o/n/e/ /d/e/i/ /q/u/i/z/./ /N/o/n/ /&/e/g/r/a/v/e/;/ /n/e/c/e/s/s/a/r/i/o/ /c/h/e/ /o/g/n/i/ /g/r/u/p/p/o/ /s/i/a/ /c/o/s/t/i/t/u/i/t/o/ /d/a/l/l/o/ /s/t/e/s/s/o/ /n/u/m/e/r/o/ /d/i/ /e/l/e/m/e/n/t/i/./ /E/&/#/3/9/;/ /a/u/s/p/i/c/a/b/i/l/e/ /c/h/e/ /l/e/ /s/c/u/o/l/e/ /c/h/e/ /i/n/t/e/n/d/o/n/o/ /p/a/r/t/e/c/i/p/a/r/e/ /c/o/n/ /p/i/&/u/g/r/a/v/e/;/ /s/q/u/a/d/r/e/ /f/o/r/m/i/n/o/ /a/n/c/h/e/ /u/n/a/ /s/q/u/a/d/r/a/ /d/i/ /s/o/l/e/ /r/a/g/a/z/z/e/:/ /&/e/g/r/a/v/e/;/ /p/r/e/v/i/s/t/o/ /u/n/ /r/i/c/o/n/o/s/c/i/m/e/n/t/o/ /p/e/r/ /l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /t/u/t/t/a/ /f/e/m/m/i/n/i/l/e/./ /E/&/#/3/9/;/ /o/p/p/o/r/t/u/n/o/ /c/h/e/ /u/n/a/ /s/q/u/a/d/r/a/ /a/b/b/i/a/ /a/ /d/i/s/p/o/s/i/z/i/o/n/e/ /u/n/&/#/3/9/;/a/u/l/a/,/ /o/ /u/n/ /l/a/b/o/r/a/t/o/r/i/o/,/ /r/i/s/e/r/v/a/t/o/ /e/s/c/l/u/s/i/v/a/m/e/n/t/e/ /a/l/l/a/ /c/o/m/p/e/t/i/z/i/o/n/e/./ /N/o/n/ /&/e/g/r/a/v/e/;/ /o/p/p/o/r/t/u/n/o/ /c/h/e/ /p/i/&/u/g/r/a/v/e/;/ /s/q/u/a/d/r/e/ /c/o/n/d/i/v/i/d/a/n/o/ /l/o/ /s/t/e/s/s/o/ /l/a/b/o/r/a/t/o/r/i/o/./ /O/g/n/i/ /s/q/u/a/d/r/a/ /d/o/v/r/e/b/b/e/ /a/v/e/r/e/ /a/ /d/i/s/p/o/s/i/z/i/o/n/e/ /t/r/e/ /c/o/m/p/u/t/e/r/ /c/o/n/n/e/s/s/i/ /c/o/n/t/e/m/p/o/r/a/n/e/a/m/e/n/t/e/ /a/ /I/n/t/e/r/n/e/t/,/ /u/n/o/ /p/e/r/ /o/g/n/i/ /g/r/u/p/p/o/./ /E/&/#/3/9/;/ /c/o/m/u/n/q/u/e/ /p/o/s/s/i/b/i/l/e/ /p/a/r/t/e/c/i/p/a/r/e/ /a/n/c/h/e/ /c/o/n/ /u/n/ /s/o/l/o/ /c/o/m/p/u/t/e/r/ /c/o/n/n/e/s/s/o/ /a/ /I/n/t/e/r/n/e/t/ /p/e/r/ /s/q/u/a/d/r/a/.////&/b/u/l/l/;/&/n/b/s/p/;//L/&/#/3/9/;/i/s/c/r/i/z/i/o/n/e/,// /c/o/m/p/l/e/t/a/m/e/n/t/e/ /g/r/a/t/u/i/t/a/,/ /p/u/&/o/g/r/a/v/e/;/ /e/s/s/e/r/e/ /e/f/f/e/t/t/u/a/t/a/ /e/s/c/l/u/s/i/v/a/m/e/n/t/e/ /d/a/l/ /d/o/c/e/n/t/e/ /r/e/f/e/r/e/n/t/e/,/ /l/&/#/3/9/;/a/l/l/e/n/a/t/o/r/e/ /d/e/l/l/a/ /s/q/u/a/d/r/a/,/ /e/ /a/v/v/i/e/n/e/ /e/s/c/l/u/s/i/v/a/m/e/n/t/e/ /c/o/m/p/i/l/a/n/d/o/ /i/l/ /m/o/d/u/l/o/ /p/r/e/s/e/n/t/e/ /n/e/l/ /s/i/t/o/ /d/e/l/l/a/ /g/a/r/a/ /(//w/w/w/./m/a/t/e/m/a/t/i/c/a/m/e/n/t/e/./i/t// /o/ //h/t/t/p/://///f/a/n/t/a/v/i/l/l/a/g/e/./r/e/p/u/b/b/l/i/c/a/./i/t///m/a/t/e/m/a/t/i/c/u/p//)/./ /A/l/ /m/o/m/e/n/t/o/ /d/e/l/l/&/#/3/9/;/i/s/c/r/i/z/i/o/n/e/ /i/l/ /d/o/c/e/n/t/e/ /r/i/c/e/v/e/r/&/a/g/r/a/v/e/;/ /p/r/e/s/s/o/ /i/l/ /s/u/o/ /i/n/d/i/r/i/z/z/o/ /e/-/m/a/i/l/ /l/a/ /p/a/s/s/w/o/r/d/ /p/e/r/ /g/l/i/ /a/l/l/e/n/a/m/e/n/t/i/ /e/ /l/e/ /p/a/s/s/w/o/r/d/ /p/e/r/ /l/a/ /g/a/r/a/./ /L/a/ /p/a/s/s/w/o/r/d/ /p/e/r/ /g/l/i/ /a/l/l/e/n/a/m/e/n/t/i/ /p/u/&/o/g/r/a/v/e/;/ /e/s/s/e/r/e/ /c/o/m/u/n/i/c/a/t/a/ /a/ /o/g/n/i/ /s/t/u/d/e/n/t/e/ /d/e/l/l/a/ /s/q/u/a/d/r/a/,/ /i/n/ /m/o/d/o/ /c/h/e/ /c/i/a/s/c/u/n/o/ /p/o/s/s/a/ /a/l/l/e/n/a/r/s/i/ /a/n/c/h/e/ /d/a/ /c/a/s/a/,/ /c/o/n/ /i/ /p/r/o/p/r/i/ /a/m/i/c/i/ /e/ /l/a/ /p/r/o/p/r/i/a/ /f/a/m/i/g/l/i/a/./ /L/e/ /p/a/s/s/w/o/r/d/ /p/e/r/ /l/a/ /g/a/r/a/ /r/e/s/t/e/r/a/n/n/o/ /c/u/s/t/o/d/i/t/e/ /d/a/l/ /d/o/c/e/n/t/e/-/a/l/l/e/n/a/t/o/r/e/ /e/ /r/e/s/t/e/r/a/n/n/o/ /s/e/g/r/e/t/e/ /f/i/n/o/ /a/l/ /g/i/o/r/n/o/ /d/e/l/l/a/ /g/a/r/a/.////&/b/u/l/l/;/&/n/b/s/p/;//I/ /q/u/i/z// /d/e/l/l/a/ /g/a/r/a/ /r/i/c/h/i/e/d/o/n/o/ /l/a/ /c/a/p/a/c/i/t/&/a/g/r/a/v/e/;/ /d/i/ /a/p/p/l/i/c/a/r/e/ /l/a/ /m/a/t/e/m/a/t/i/c/a/ /n/e/l/l/a/ /v/i/t/a/ /d/i/ /t/u/t/t/i/ /i/ /g/i/o/r/n/i/./ /I/ /c/o/n/t/e/s/t/i/ /d/e/i/ /q/u/i/z/ /r/i/g/u/a/r/d/a/n/o/ /i/ /s/e/g/u/e/n/t/i/ /a/m/b/i/t/i/:/ /p/e/r/s/o/n/a/l/e/,/ /f/a/m/i/l/i/a/r/e/,/ /s/c/o/l/a/s/t/i/c/o/,/ /s/p/o/r/t/,/ /l/a/v/o/r/o/,/ /e/c/o/n/o/m/i/a/,/ /p/u/b/b/l/i/c/o/-/s/o/c/i/a/l/e/,/ /s/c/i/e/n/z/a/ /e/ /t/e/c/n/o/l/o/g/i/a/./ /I/ /t/e/m/i/ /d/i/ /m/a/t/e/m/a/t/i/c/a/ /f/a/n/n/o/ /r/i/f/e/r/i/m/e/n/t/o/ /a/l/l/e/ /r/e/c/e/n/t/i/ /I/n/d/i/c/a/z/i/o/n/i/ /p/e/r/ /i/l/ /C/u/r/r/i/c/o/l/o/ /e/ /r/i/g/u/a/r/d/a/n/o/&/n/b/s/p/;/ /l/e/ /s/e/g/u/e/n/t/i/ /a/r/e/e/:/ /n/u/m/e/r/i/ /e/ /r/e/l/a/z/i/o/n/i/ /(/a/r/i/t/m/e/t/i/c/a/ /e/ /a/l/g/e/b/r/a/)/,/ /s/p/a/z/i/o/,/ /f/i/g/u/r/e/ /e/ /m/i/s/u/r/e/ /(/g/e/o/m/e/t/r/i/a/)/,/ /d/a/t/i/ /e/ /p/r/e/v/i/s/i/o/n/i/ /(/s/t/a/t/i/s/t/i/c/a/ /e/ /p/r/o/b/a/b/i/l/i/t/&/a/g/r/a/v/e/;/)/,/ /l/o/g/i/c/a/ /e/ /t/e/o/r/i/a/ /e/l/e/m/e/n/t/a/r/e/ /d/e/g/l/i/ /i/n/s/i/e/m/i/.////&/b/u/l/l/;/&/n/b/s/p/;//G/l/i/ /a/l/l/e/n/a/m/e/n/t/i// /p/o/s/s/o/n/o/ /e/s/s/e/r/e/ /f/a/t/t/i/ /i/n/ /q/u/a/l/s/i/a/s/i/ /m/o/m/e/n/t/o/ /s/i/a/ /a/ /s/c/u/o/l/a/ /s/i/a/ /f/u/o/r/i/ /d/a/l/l/a/ /s/c/u/o/l/a/./ /I/ /q/u/e/s/i/t/i/ /s/o/n/o/ /a/n/a/l/o/g/h/i/ /a/ /q/u/e/l/l/i/ /d/e/l/l/a/ /g/a/r/a/ /e/ /i/ /p/u/n/t/e/g/g/i/ /s/o/n/o/ /c/a/l/c/o/l/a/t/i/ /a/l/l/o/ /s/t/e/s/s/o/ /m/o/d/o/.////&/b/u/l/l/;/&/n/b/s/p/;//L/a/ /g/a/r/a// /s/i/ /s/v/o/l/g/e/ /i/n/ /u/n/&/#/3/9/;/u/n/i/c/a/ /s/e/s/s/i/o/n/e/ /d/a/l/l/e/ /9/./0/0/ /a/l/l/e/ /1/2/./3/0/ /d/e/l/ /g/i/o/r/n/o/ /7/ /m/a/g/g/i/o/ /2/0/0/8/./ /D/a/l/l/e/ /9/./0/0/ /a/l/l/e/ /9/./3/0/ /i/ /c/o/n/c/o/r/r/e/n/t/i/ /p/r/e/n/d/e/r/a/n/n/o/ /p/o/s/t/o/ /s/u/d/d/i/v/i/s/i/ /i/n/ /t/r/e/ /g/r/u/p/p/i/,/ /c/i/a/s/c/u/n/o/ /d/a/v/a/n/t/i/ /a/l/ /p/r/o/p/r/i/o/ /c/o/m/p/u/t/e/r/ /d/i/ /g/a/r/a/ /e/ /c/i/a/s/c/u/n/o/ /c/o/n/ /i/l/ /p/r/o/p/r/i/o/ /r/u/o/l/o/:/ /c/a/p/i/t/a/n/o/,/ /o/p/e/r/a/t/o/r/e/,/ /r/i/s/o/l/u/t/o/r/e/./ /L/o/ /s/t/u/d/e/n/t/e/ /a/d/d/e/t/t/o/ /a/l/ /c/o/m/p/u/t/e/r/ /i/n/s/e/r/i/r/&/a/g/r/a/v/e/;/ /l/a/ /p/a/s/s/w/o/r/d/ /d/i/ /g/a/r/a/ /d/e/l/ /p/r/o/p/r/i/o/ /g/r/u/p/p/o/./ /L/e/ /s/q/u/a/d/r/e/ /c/h/e/ /p/a/r/t/e/c/i/p/a/n/o/ /c/o/n/ /u/n/ /s/o/l/o/ /c/o/m/p/u/t/e/r/ /i/n/s/e/r/i/r/a/n/n/o/ /s/o/l/o/ /l/a/ /p/r/i/m/a/ /p/a/s/s/w/o/r/d/ /d/i/ /g/a/r/a/ /e/ /s/c/e/g/l/i/e/r/a/n/n/o/ /l/&/#/3/9/;/o/p/z/i/o/n/e/ /&/q/u/o/t/;/1/ /P/C/&/q/u/o/t/;/./ /A/ /p/a/r/t/i/r/e/ /d/a/l/l/e/ /9/./3/0/ /a/p/p/a/r/i/r/a/n/n/o/ /i/ /q/u/i/z/,/ /p/r/e/c/i/s/a/m/e/n/t/e/ /s/u/l/ /c/o/m/p/u/t/e/r/ /d/e/l/l/a/ /c/l/a/s/s/e/ /p/r/i/m/a/ /c/o/m/p/a/r/i/r/a/n/n/o/ /s/o/l/o/ /i/ /q/u/e/s/i/t/i/ /c/h/e/ /d/e/v/o/n/o/ /e/s/s/e/r/e/ /r/i/s/o/l/t/i/ /d/a/g/l/i/ /s/t/u/d/e/n/t/i/ /d/i/ /p/r/i/m/a/,/ /s/u/ /q/u/e/l/l/o/ /d/e/l/l/a/ /c/l/a/s/s/e/ /s/e/c/o/n/d/a/ /c/o/m/p/a/r/i/r/a/n/n/o/ /s/o/l/o/ /i/ /q/u/e/s/i/t/i/ /d/e/l/l/a/ /s/e/c/o/n/d/a/ /e/ /c/o/s/&/i/g/r/a/v/e/;/ /v/i/a/ /p/e/r/ /l/a/ /t/e/r/z/a/ /c/l/a/s/s/e/./ /L/a/ /s/q/u/a/d/r/a/ /c/h/e/ /p/a/r/t/e/c/i/p/a/ /c/o/n/ /u/n/ /s/o/l/o/ /c/o/m/p/u/t/e/r/ /a/v/r/&/a/g/r/a/v/e/;/ /s/u/l/l/o/ /s/t/e/s/s/o/ /c/o/m/p/u/t/e/r/ /i/ /q/u/e/s/i/t/i/ /d/i/ /I/,/ /I/I/,/ /I/I/I/ /c/l/a/s/s/e/./ /I/n/ /c/a/s/o/ /d/i/ /r/i/t/a/r/d/i/ /e/ /p/r/o/b/l/e/m/i/ /t/e/c/n/i/c/i/ /d/o/v/u/t/i/ /a/l/l/a/ /s/c/u/o/l/a/ /p/a/r/t/e/c/i/p/a/n/t/e/,/ /l/a/ /s/q/u/a/d/r/a/ /s/v/o/l/g/e/r/&/a/g/r/a/v/e/;/ /u/g/u/a/l/m/e/n/t/e/ /l/a/ /g/a/r/a/,/ /c/h/e/ /c/o/m/u/n/q/u/e/ /s/i/ /c/o/n/c/l/u/d/e/r/&/a/g/r/a/v/e/;/ /p/e/r/ /t/u/t/t/i/ /i/ /c/o/n/c/o/r/r/e/n/t/i/ /a/l/l/e/ /1/2/./3/0/./ /O/g/n/i/ /s/t/u/d/e/n/t/e/ /d/u/r/a/n/t/e/ /l/o/ /s/v/o/l/g/i/m/e/n/t/o/ /d/e/l/l/a/ /g/a/r/a/ /c/o/l/l/a/b/o/r/a/ /c/o/n/ /i/l/ /p/r/o/p/r/i/o/ /g/r/u/p/p/o/ /p/e/r/ /c/e/r/c/a/r/e/ /d/i/ /r/i/s/o/l/v/e/r/e/ /c/o/r/r/e/t/t/a/m/e/n/t/e/ /n/e/l/ /m/i/n/o/r/ /t/e/m/p/o/ /p/o/s/s/i/b/i/l/e/ /i/l/ /m/a/g/g/i/o/r/ /n/u/m/e/r/o/ /d/i/ /q/u/i/z/./ /P/u/&/o/g/r/a/v/e/;/ /u/t/i/l/i/z/z/a/r/e/,/ /c/a/l/c/o/l/a/t/r/i/c/i/,/ /s/o/f/t/w/a/r/e/,/ /l/i/b/r/i/ /e/ /q/u/a/n/t/&/#/3/9/;/a/l/t/r/o/ /r/i/t/i/e/n/e/ /n/e/c/e/s/s/a/r/i/o/;/ /n/o/n/ /p/u/&/o/g/r/a/v/e/;/ /c/o/m/u/n/i/c/a/r/e/ /n/&/e/a/c/u/t/e/;/ /a/ /v/o/c/e/,/ /n/&/e/a/c/u/t/e/;/ /a/l/ /t/e/l/e/f/o/n/o/,/ /n/&/e/a/c/u/t/e/;/ /i/n/ /c/h/a/t/,/ /n/&/e/a/c/u/t/e/;/ /p/e/r/ /e/-/m/a/i/l/ /c/o/n/ /p/e/r/s/o/n/e/ /c/h/e/ /n/o/n/ /f/a/n/n/o/ /p/a/r/t/e/ /d/e/l/l/a/ /p/r/o/p/r/i/a/ /s/q/u/a/d/r/a/,/ /n/o/n/ /p/u/&/o/g/r/a/v/e/;/ /c/h/i/e/d/e/r/e/ /a/i/u/t/o/ /a/l/ /p/r/o/p/r/i/o/ /a/l/l/e/n/a/t/o/r/e/ /p/e/r/ /l/a/ /r/i/s/o/l/u/z/i/o/n/e/ /d/e/g/l/i/ /e/s/e/r/c/i/z/i/.////&/b/u/l/l/;/&/n/b/s/p/;//L/a/ /v/a/l/u/t/a/z/i/o/n/e// /d/e/i/ /q/u/e/s/i/t/i/ /&/e/g/r/a/v/e/;/ /e/f/f/e/t/t/u/a/t/a/ /s/i/a/ /i/n/ /b/a/s/e/ /a/l/ /l/i/v/e/l/l/o/ /d/i/ /d/i/f/f/i/c/o/l/t/&/a/g/r/a/v/e/;/ /d/e/l/ /q/u/e/s/i/t/o/ /s/i/a/ /i/n/ /b/a/s/e/ /a/l/ /t/e/m/p/o/ /i/m/p/i/e/g/a/t/o/ /p/e/r/ /r/i/s/o/l/v/e/r/l/o/./ /P/e/r/ /c/i/a/s/c/u/n/ /q/u/i/z/ /v/i/e/n/e/ /i/n/d/i/c/a/t/o/ /i/l/ /l/i/v/e/l/l/o/ /d/i/ /d/i/f/f/i/c/o/l/t/&/a/g/r/a/v/e/;/,/ /d/a/ /1/ /a/ /5/,/ /e/s/p/r/e/s/s/o/ /g/r/a/f/i/c/a/m/e/n/t/e/ /i/n/ /s/t/e/l/l/i/n/e/./ /D/a/ /q/u/a/n/d/o/ /i/l/ /q/u/i/z/ /v/i/e/n/e/ /a/p/e/r/t/o/ /c/i/ /s/o/n/o/ /2/ /m/i/n/u/t/i/ /d/i/ /t/e/m/p/o/ /p/e/r/ /l/e/g/g/e/r/l/o/ /c/o/n/ /a/t/t/e/n/z/i/o/n/e/ /e/ /d/i/s/c/u/t/e/r/l/o/ /c/o/n/ /i/ /c/o/m/p/a/g/n/i/ /d/i/ /s/q/u/a/d/r/a/./ /D/u/r/a/n/t/e/ /q/u/e/s/t/o/ /t/e/m/p/o/ /i/l/ /c/o/m/p/u/t/e/r/ /n/o/n/ /a/c/c/e/t/t/e/r/&/a/g/r/a/v/e/;/ /l/a/ /r/i/s/p/o/s/t/a/,/ /p/e/r/t/a/n/t/o/ /&/e/g/r/a/v/e/;/ /i/n/u/t/i/l/e/ /r/i/s/p/o/n/d/e/r/e/ /a/ /u/n/ /q/u/i/z/ /i/n/ /t/u/t/t/a/ /f/r/e/t/t/a/ /s/e/n/z/a/ /a/v/e/r/ /l/e/t/t/o/ /e/ /d/i/s/c/u/s/s/o/ /c/o/n/ /i/ /c/o/m/p/a/g/n/i/ /d/i/ /g/r/u/p/p/o/./ /D/o/p/o/ /i/ /2/ /m/i/n/u/t/i/ /d/i/ /l/e/t/t/u/r/a/ /e/ /c/o/n/d/i/v/i/s/i/o/n/e/ /d/e/l/ /q/u/i/z/,/ /p/a/r/t/i/r/&/a/g/r/a/v/e/;/ /u/n/ /c/r/o/n/o/m/e/t/r/o/ /c/h/e/ /s/i/ /f/e/r/m/e/r/&/a/g/r/a/v/e/;/ /q/u/a/n/d/o/ /l/&/#/3/9/;/a/d/d/e/t/t/o/ /a/l/ /c/o/m/p/u/t/e/r/ /i/n/s/e/r/i/s/c/e/ /e/ /c/o/n/f/e/r/m/a/ /l/a/ /r/i/s/p/o/s/t/a/ /i/n/ /m/a/n/i/e/r/a/ /d/e/f/i/n/i/t/i/v/a/./ /I/l/ /t/e/m/p/o/ /d/i/ /r/i/s/o/l/u/z/i/o/n/e/ /d/e/l/l/&/#/3/9/;/e/s/e/r/c/i/z/i/o/ /e/ /q/u/i/n/d/i/ /i/l/ /p/u/n/t/e/g/g/i/o/ /o/t/t/e/n/u/t/o/ /n/o/n/ /d/i/p/e/n/d/e/ /d/a/l/l/a/ /v/e/l/o/c/i/t/&/a/g/r/a/v/e/;/ /d/i/ /c/o/n/n/e/s/s/i/o/n/e/ /d/e/l/ /c/o/m/p/u/t/e/r/ /d/i/ /g/a/r/a/ /m/a/ /e/s/c/l/u/s/i/v/a/m/e/n/t/e/ /d/a/l/ /t/e/m/p/o/ /i/n/t/e/r/c/o/r/s/o/ /t/r/a/ /q/u/a/n/d/o/ /i/l/ /c/o/m/p/u/t/e/r/ /h/a/ /r/i/c/e/v/u/t/o/ /i/l/ /q/u/e/s/i/t/o/ /e/ /q/u/a/n/d/o/ /&/e/g/r/a/v/e/;/ /s/t/a/t/o/ /p/r/e/m/u/t/o/ /i/l/ /b/o/t/t/o/n/e/ /d/i/ /c/o/n/f/e/r/m/a/ /d/e/l/l/a/ /s/o/l/u/z/i/o/n/e/./ /I/l/ /p/u/n/t/e/g/g/i/o/ /p/e/r/ /c/i/a/s/c/u/n/ /q/u/i/z/ /p/a/r/t/e/ /d/a/l/ /l/i/v/e/l/l/o/ /d/i/ /d/i/f/f/i/c/o/l/t/&/a/g/r/a/v/e/;/ /d/e/l/ /q/u/e/s/i/t/o/ /e/ /d/i/m/i/n/u/i/s/c/e/ /c/o/n/ /i/l/ /t/r/a/s/c/o/r/r/e/r/e/ /d/e/l/ /t/e/m/p/o/ /f/i/n/o/ /a/l/l/a/ /c/o/n/f/e/r/m/a/ /d/e/l/l/a/ /r/i/s/p/o/s/t/a/./ /I/l/ /p/u/n/t/e/g/g/i/o/ /d/e/l/l/a/ /s/q/u/a/d/r/a/ /s/a/r/&/a/g/r/a/v/e/;/ /d/a/t/o/ /d/a/l/l/a/ /s/o/m/m/a/ /d/e/i/ /p/u/n/t/e/g/g/i/ /d/e/i/ /q/u/i/z/ /r/i/s/o/l/t/i/ /d/a/ /o/g/n/i/ /g/r/u/p/p/o/./ /L/a/ /c/l/a/s/s/i/f/i/c/a/ /v/i/e/n/e/ /e/l/a/b/o/r/a/t/a/ /c/o/n/t/e/m/p/o/r/a/n/e/a/m/e/n/t/e/ /a/l/l/a/ /p/r/o/v/a/ /e/ /p/u/&/o/g/r/a/v/e/;/ /e/s/s/e/r/e/ /v/i/s/u/a/l/i/z/z/a/t/a/ /i/n/ /q/u/a/l/s/i/a/s/i/ /m/o/m/e/n/t/o/ /d/e/l/l/a/ /g/a/r/a/.////&/b/u/l/l/;/&/n/b/s/p/;//I/l/ /d/o/c/e/n/t/e/ /r/e/f/e/r/e/n/t/e// /&/e/g/r/a/v/e/;/ /r/e/s/p/o/n/s/a/b/i/l/e/ /d/e/l/l/a/ /v/a/l/e/n/z/a/ /d/i/d/a/t/t/i/c/a/ /d/e/l/l/&/#/3/9/;/i/n/i/z/i/a/t/i/v/a/,/ /s/i/a/ /n/e/i/ /c/o/n/f/r/o/n/t/i/ /d/e/i/ /p/r/o/p/r/i/ /s/t/u/d/e/n/t/i/ /s/i/a/ /n/e/i/ /c/o/n/f/r/o/n/t/i/ /d/e/g/l/i/ /o/r/g/a/n/i/z/z/a/t/o/r/i/ /d/e/l/l/a/ /g/a/r/a/ /e/ /s/c/o/r/a/g/g/e/r/&/a/g/r/a/v/e/;/ /e/v/e/n/t/u/a/l/i/ /c/o/m/p/o/r/t/a/m/e/n/t/i/ /a/n/t/i/s/p/o/r/t/i/v/i/ /d/e/i/ /p/r/o/p/r/i/ /a/l/l/i/e/v/i/./ /D/u/r/a/n/t/e/ /l/a/ /g/a/r/a/,/ /l/&/#/3/9/;/a/l/l/e/n/a/t/o/r/e/ /p/u/&/o/g/r/a/v/e/;/ /c/o/n/n/e/t/t/e/r/s/i/ /s/u/ /u/n/ /a/l/t/r/o/ /c/o/m/p/u/t/e/r/ /n/o/n/ /u/t/i/l/i/z/z/a/t/o/ /p/e/r/ /l/a/ /g/a/r/a/ /p/e/r/ /v/i/s/u/a/l/i/z/z/a/r/e/ /i/n/ /t/e/m/p/o/ /r/e/a/l/e/ /l/a/ /c/l/a/s/s/i/f/i/c/a/ /g/e/n/e/r/a/l/e/ /e/ /i/n/c/o/r/a/g/g/i/a/r/e/ /l/a/ /p/r/o/p/r/i/a/ /s/q/u/a/d/r/a/ /a/d/ /o/t/t/e/n/e/r/e/ /l/a/ /p/r/e/s/t/a/z/i/o/n/e/ /m/a/s/s/i/m/a/.////&/b/u/l/l/;/&/n/b/s/p/;//L/a/ /p/r/o/c/l/a/m/a/z/i/o/n/e// /d/e/i/ /v/i/n/c/i/t/o/r/i/ /a/v/v/e/r/r/&/a/g/r/a/v/e/;/ /i/l/ /9/ /m/a/g/g/i/o/ /2/0/0/8/./ /P/e/r/ /t/u/t/t/e/ /l/e/ /s/q/u/a/d/r/e/ /c/h/e/ /s/i/ /s/a/r/a/n/n/o/ /q/u/a/l/i/f/i/c/a/t/e/ /a/i/ /p/r/i/m/i/ /p/o/s/t/i/,/ /l/a/ /g/i/u/r/i/a/ /a/c/c/e/r/t/e/r/&/a/g/r/a/v/e/;/ /c/h/e/ /l/&/r/s/q/u/o/;/i/s/c/r/i/z/i/o/n/e/ /a/l/l/a/ /g/a/r/a/ /s/i/a/ /s/t/a/t/a/ /c/o/n/f/o/r/m/e/ /a/l/l/e/ /r/e/g/o/l/e/,/ /i/l/ /d/o/c/e/n/t/e/ /r/e/f/e/r/e/n/t/e/ /c/o/n/f/e/r/m/e/r/&/a/g/r/a/v/e/;/ /c/h/e/ /l/e/ /r/e/g/o/l/e/ /d/i/ /g/a/r/a/ /s/o/n/o/ /s/t/a/t/e/ /p/i/e/n/a/m/e/n/t/e/ /r/i/s/p/e/t/t/a/t/e/ /d/a/g/l/i/ /a/l/u/n/n/i/ /d/e/l/l/a/ /p/r/o/p/r/i/a/ /s/q/u/a/d/r/a/./ /P/e/r/ /i/l/ /r/e/g/o/l/a/r/e/ /s/v/o/l/g/i/m/e/n/t/o/ /d/e/l/l/e/ /g/a/r/a/,/ /l/a/ /g/i/u/r/i/a/ /s/i/ /a/f/f/i/d/a/ /a/l/ /s/e/n/s/o/ /d/i/ /s/p/o/r/t/i/v/i/t/&/a/g/r/a/v/e/;/ /e/ /p/r/o/f/e/s/s/i/o/n/a/l/i/t/&/a/g/r/a/v/e/;/ /d/e/i/ /p/r/o/f/e/s/s/o/r/i/ /e/ /d/e/g/l/i/ /a/l/u/n/n/i/.////S/a/r/a/n/n/o/ /p/r/e/m/i/a/t/e/:////l/a/ /s/q/u/a/d/r/a/ /c/h/e/ /h/a/ /o/t/t/e/n/u/t/o/ /i/l/ /p/u/n/t/e/g/g/i/o/&/n/b/s/p/;/ /m/a/s/s/i/m/o//l/a/ /s/q/u/a/d/r/a/ /s/e/c/o/n/d/a/ /c/l/a/s/s/i/f/i/c/a/t/a//l/a/ /s/q/u/a/d/r/a/ /t/e/r/z/a/ /c/l/a/s/s/i/f/i/c/a/t/a//l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /f/e/m/m/i/n/i/l/e/,//l/a/ /m/i/g/l/i/o/r/e/ /s/c/u/o/l/a/,/ /q/u/e/l/l/a/ /c/h/e/ /h/a/ /o/t/t/e/n/u/t/o/ /i/l/ /p/u/n/t/e/g/g/i/o/ /m/a/s/s/i/m/o/ /d/a/t/o/ /d/a/l/l/a/ /s/o/m/m/a/ /d/e/i/ /p/u/n/t/e/g/g/i/ /d/i/ /t/u/t/t/e/ /l/e/ /s/q/u/a/d/r/e/ /p/r/e/s/e/n/t/a/t/e/.////U/l/t/e/r/i/o/r/i/ /r/i/c/o/n/o/s/c/i/m/e/n/t/i/,/ /n/o/n/ /c/u/m/u/l/a/b/i/l/i/ /c/o/n/ /i/ /p/r/e/c/e/d/e/n/t/i/,/ /s/a/r/a/n/n/o/ /a/s/s/e/g/n/a/t/i/ /a/:////l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /n/e/g/l/i/ /a/l/l/e/n/a/m/e/n/t/i/.//l/a/ /m/i/g/l/i/o/r/e/ /c/l/a/s/s/e/ /p/r/i/m/a/,//l/a/ /m/i/g/l/i/o/r/e/ /c/l/a/s/s/e/ /s/e/c/o/n/d/a/,//l/a/ /m/i/g/l/i/o/r/e/ /c/l/a/s/s/e/ /t/e/r/z/a/,//l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /i/n/ /A/r/i/t/m/e/t/i/c/a/ /e/ /A/l/g/e/b/r/a/,//l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /i/n/ /G/e/o/m/e/t/r/i/a/,//l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /i/n/ /L/o/g/i/c/a/,//l/a/ /m/i/g/l/i/o/r/e/ /s/q/u/a/d/r/a/ /i/n/ /S/t/a/t/i/s/t/i/c/a/ /e/ /p/r/o/b/a/b/i/l/i/t/&/a/g/r/a/v/e/;/.////&/n/b/s/p/;//2006 – liceo scientifico sperimentale, sessione straordinaria
55. Lo sviluppo storico del concetto di funzione e le origini della teoria delle distribuzioni
 In questo articolo, che contiene una sintesi del mio libro Lo sviluppo storico del concetto di funzione e le origini della teoria delle distribuzioni, mi sono proposto di valutare le motivazioni che determinarono lo sviluppo storico del concetto di funzione e che diedero origine alla teoria delle distribuzioni, evidenziando la differenza che intercorre fra la matematica come sistema organicamente strutturato e come disciplina in fieri: la matematica, nel corso del suo sviluppo storico, sembra infatti molto più simile a una scienza sperimentale, che all’impalcatura ipotetico-deduttiva cui siamo abituati; quest’ultima appartiene alla fase di riorganizzazione logica delle teorie, più che al momento della scoperta vera e propria.
In questo articolo, che contiene una sintesi del mio libro Lo sviluppo storico del concetto di funzione e le origini della teoria delle distribuzioni, mi sono proposto di valutare le motivazioni che determinarono lo sviluppo storico del concetto di funzione e che diedero origine alla teoria delle distribuzioni, evidenziando la differenza che intercorre fra la matematica come sistema organicamente strutturato e come disciplina in fieri: la matematica, nel corso del suo sviluppo storico, sembra infatti molto più simile a una scienza sperimentale, che all’impalcatura ipotetico-deduttiva cui siamo abituati; quest’ultima appartiene alla fase di riorganizzazione logica delle teorie, più che al momento della scoperta vera e propria.
56. Impostazione algebrica dell’analisi matematica
 Continuare ad insegnare l’Analisi Matematica, ovvero ciò che gli anglosassoni chiamano Calculus, così come si faceva nel ‘900, senza tener conto dei computer e dei software come TI InterActive! TI-nspire e simili, assomiglia a certi comportamenti sociali che il politicamente corretto evita di esplicitare, se non si vuole essere tacciati di fascista e razzista. Una recente pubblicità della Microsoft fa vedere gli impiegati Dino e Saura con la faccia da animali preistorici e li invita ad aggiornarsi. Noi ci stiamo provando da circa dieci anni con i docenti di matematica a ogni livello, purtroppo i risultati sono deludenti. Il termine matematica da rottamare, coniato nel 1997, sembra sia stato allegramente ignorato dai sacerdoti del sapere e accettato solo per alcuni argomenti ovvii.
Continuare ad insegnare l’Analisi Matematica, ovvero ciò che gli anglosassoni chiamano Calculus, così come si faceva nel ‘900, senza tener conto dei computer e dei software come TI InterActive! TI-nspire e simili, assomiglia a certi comportamenti sociali che il politicamente corretto evita di esplicitare, se non si vuole essere tacciati di fascista e razzista. Una recente pubblicità della Microsoft fa vedere gli impiegati Dino e Saura con la faccia da animali preistorici e li invita ad aggiornarsi. Noi ci stiamo provando da circa dieci anni con i docenti di matematica a ogni livello, purtroppo i risultati sono deludenti. Il termine matematica da rottamare, coniato nel 1997, sembra sia stato allegramente ignorato dai sacerdoti del sapere e accettato solo per alcuni argomenti ovvii.
58. La matematica in Italia, interviste
 In occasione del recente congresso dell’UMI a Bari (24-29 set. 2007) abbiamo incontrato alcuni dei partecipanti e abbiamo chiesto loro di parlarci della situazione della matematica in Italia, sia per quanto riguarda la ricerca sia per quanto riguarda la didattica. Le risposte che abbiamo riportato sono quelle di Italo Capuzzo Dolcetta, Eugenio Ragazzini e Domenico Lenzi.
In occasione del recente congresso dell’UMI a Bari (24-29 set. 2007) abbiamo incontrato alcuni dei partecipanti e abbiamo chiesto loro di parlarci della situazione della matematica in Italia, sia per quanto riguarda la ricerca sia per quanto riguarda la didattica. Le risposte che abbiamo riportato sono quelle di Italo Capuzzo Dolcetta, Eugenio Ragazzini e Domenico Lenzi.
2007 – liceo scientifico – scuole italiane all’estero (Europa)
 Tema di matematica svolto assegnato all’esame di maturità per il liceo scientifico nelle scuole italiane all’estero (Europa)
Tema di matematica svolto assegnato all’esame di maturità per il liceo scientifico nelle scuole italiane all’estero (Europa)
CONCORSO “Miglior tesina del 2007”: Davide Gerosa vince il primo premio
 Davide Gerosa è il vincitore del primo premio per la “Migliore tesina 2007” con una tesina sulla materia oscura giudicata valida anche da ricercatori del settore. Nella foto è ritratto con il MacBook e la targa del premio. Di seguito riportiamo alcune parti dell’intervista che gli abbiamo fatto.
Davide Gerosa è il vincitore del primo premio per la “Migliore tesina 2007” con una tesina sulla materia oscura giudicata valida anche da ricercatori del settore. Nella foto è ritratto con il MacBook e la targa del premio. Di seguito riportiamo alcune parti dell’intervista che gli abbiamo fatto.
. . .
Cosa ti ha spinto a scegliere questo argomento per l’elaborazione della tua tesina?
Il cielo e le stelle mi hanno sempre appassionato, fin da piccolo. Quest’anno, ho avuto la possibilità di studiare con metodo ciò che prima curiosavo sui libri. Molto più di recente invece ho maturato un certo interesse per la cosmologia. Credo che tutti gli uomini siano accomunati dalle grandi domande esistenziali (Chi siamo? Come siamo venuti al mondo? Dove andiamo?). Anche se le risposte sono diverse (filosofiche, sicnetifiche) e spesso inconcludenti, la domanda ci accomuna. Lavorare su un argomento così quindi permette di conoscere come l’uomo ha cercato di rispondere a queste domande: il tutto utilizzando il linguaggio della matematica. La scelta della materia oscura in particolare è dovuta al fatto che le ricerche in merito non sono concluse. Mi piace avere un’idea della scienza come qualcosa di non finito, che deve ancora dirci qualcosa di nuovo. Questo argomento si presta benissimo infatti, molte sono i passi ormai compiuti, ma molti di più quelli ancora da scoprire.
Hai partecipato a qualche particolare progetto scolastico sull’argomento?
No, non in particolare. Vedendo che spesso uscivano notizie nuove su ritrovamenti di materia oscura, ho iniziato a cercare di capire un po’ cosa fosse. L’esame di stato mi ha permesso di raccogliere e approfondire tutte le varie “ultime notizie” in merito.

Come è andata la maturità? Sei stato soddisfatto del risultato finale? La commissione ha apprezzato la tua tesina?
La maturità? Benissimo. Esco dal liceo scientifico statale Frisi di Monza con 100. La tesina ha giocato un ruolo importante nell’esame. Nonostante i docenti di matematica e fisica e di scienze, diretti interessati per l’argomento del mio lavoro, fossero esterni, la tesina è stata apprezzata moltissimo. Durante il colloquio infatti, nonostante avessi a disposizione 10 minuti per l’esposizione, al termine di questi mi sono state rivolte molte domande in merito dai due professori interessati (e anche uno strano collegamento in filosofia…)
Quali progetti hai per il prossimo futuro (università, lavoro, passioni, etc.)?
Quest’anno comincio il corso di Fisica all’università degli studi di Milano. Sicuramente la tesina è stato una grande occasione per confermare questa aspirazione. Lavoro… per il momento niente di serio, magari qualche ripetizione. Mi piacerebbe scrivere, magari su un rivista scientifica. Le passioni non cambiano dopo la maturità… mi piace guardare le stelle, sono un appassionato di Tolkien e un fanatico di Bruce Springsteen.
Infine, cosa pensi di questa iniziativa organizzata da StudentVille.it e Matematicamente.it con il supporto di University.it? La ritieni utile? Per chi?
Mi sento molto gratificato da questa iniziativa, in quanto è stato dato un riconoscimento a questo mio lavoro per il quale ho speso molto tempo. Basta solo che le ricerche pubblicate sui siti siano lette come incoraggiamento e spunto per lavorare e non per trovare una tesina già pronta in vista dell’esame, come purtroppo molti cercano di fare. Dico “purtroppo” perché sono loro i primi a perdere un occasione di scoperta che la prospettiva di organizzare un lavoro completo come una tesina offre.
Somma di numeri relativi, sfida il computer: GIOCO
|
|
Fai click sul pulsante PARTENZA, scrivi il risultato nella casella apposita (senza spazi), fai click su VAI. Attento, il tempo influenza il risultato. Le domande sono 20.
Risposte esatte: |
Le torri di Hanoi (gioco Excel)
Scarica il file in formato XLS (Excel)
Ti indovino il numero (gioco Excel)
Scarica il file in formato XLS (Excel)
Lettura del pensiero 1
Scala 21
9° convegno nazionale ADT
 Modelli e Tecnologie per la Didattica della Matematica e delle Scienze Sperimentali
Modelli e Tecnologie per la Didattica della Matematica e delle Scienze Sperimentali
Esperienze documentate sul guadagno formativo nel loro uso in classe
16-17-18 novembre 2007, Grand Hotel Telese, via Cerreto1, Telese Terme (BN)
Comitato Scientifico: Paolo Boieri, Mauro Cerasoli, Aurelia Orlandoni, Giovanni Pezzi
Comitato Organizzatore: Domenico Cariello, Mauro Cerasoli, Domenica Di Sorbo, Eugenio Mercuri
Programma
Venerdì 16 novembre
14:00 Iscrizioni e apertura del convegno
14:45 Intervento del Dott. Gaetano Pascarella Sottosegretario alla Pubblica Istruzione
15:00-15:40 Mario Fierli La scuola come laboratorio delle scienze
15:50-16:30 Domenica Di Sorbo Matematica e Scienze Sperimentali
16:40 Aurelia Orlandoni Le prove PISA: un’occasione didattica
17:00 Intervallo
17:30-18:10 Mauro Cerasoli La matematica di TI-nspire
18:20 Francesco di Paola Bruno Dal gioco della zara ai nuovi dadi da portare in classe
18:40-19:00 Giovanni Pezzi Quale fisica con TI-nspire
Sabato 17 novembre
9:00 Carlo Costabile Una sperimentazione con le calcolatrici simboliche in un corso universitario di Calcolo
Integrale.
9:20 Anna Salvadori Modellizzazione matematica con strumenti elementari (un bilancio di 13 anni di
sperimentazione)
9:40 Primo Brandi I saperi del cittadino: i modelli matematici in elettricità (dalla pila di Volta all’effetto foto-voltaico)
10:00-10:40 Rocco Fazio La sperimentazione di TI-nspire nelle classi pilota
10:50 Intervallo
11:20-11:50 Sebastiano Cappuccio Presentazione di TI-nspire
12:00-12:30 Giovanni Margiotta Il piano [email protected]: un’occasione per fare "ricerca didattica" in classe
12:40-13:00 Mirella Rafanelli LabPro e LoggerPro nel Progetto Lauree Scientifiche a Lecce
Intervallo pranzo
15:00 Paolo Boieri I test d’ingresso a ingegneria
15:20 Giacomo Torzo Il “miglior laboratorio portatile” è ancora Voyage200 ( o TI-89) + LabPro (o
CBL2)
15:40 Alfio Pelli Orbite dei satelliti galileiani e massa di Giove
16:00-16:50 Clementina D’Amico, Maria Grazia Rubino Fisica in real time con TI-nspire
17:00 Intervallo
17:30-18:10 Isabella Soletta Le potenzialità di TI-nspire nell’insegnamento della fisica e della matematica
Alcuni esempi sviluppati per una classe pilota
18:20 Domenico Cariello Analisi Numerica con TI-nspire
18:40 Mario Persico www.matemagica.it una nuova tipologia di sito dedicato all’insegnamento della matematica e
delle scienze integrate con le tecnologie
19:00-19:20 Nicoletta Nolli Integrazione e dinamicità, comprendere e apprendere la matematica con TI-nspire
16:00 Finale delle Gare di Matematica con le Tecnologie; 20:30 Cena di gala
Domenica 18 novembre
9:00 Anna Alfieri Trasformazioni geometriche e frattali IFS
9:20 Tiziana Bindo Le curve celebri con TI-nspire
9:40 Roberto Ricci Le componenti individuali e di scuola nel rendimento di matematica secondo la ricerca
OCSE-PISA – L’impatto della tecnologia e degli stili di apprendimento
10:00-10:40 Luigi Tomasi Dieci anni con Cabri in classe: quale guadagno formativo per la matematica?
10:50 Intervallo
11:10-11:50 Domingo Paola TI-nspire ispira gli studenti? Analisi di una sperimentazione
12:00-13:00 Assemblea dei soci ADT.
Informazioni
L’iscrizione avviene durante il convegno; sono gradite le prenotazioni all'indirizzo [email protected] . Ai partecipanti è richiesto un contributo volontario alle spese di organizzazione di 30€ (ridotto a 20€ per i soci ADT e per gli iscritti alle SSIS). Per tutti coloro che si iscriveranno ad ADT, la quota per il 2007 è di €10.00. Al termine dei lavori, ADT rilascerà un attestato di aggiornamento in base alla CM 376, prot. 15218, del 23-12-1995 e successive modifiche. Al fine di partecipare al convegno il MPI concede l’esonero dal servizio per insegnanti di ogni ordine e grado, per il personale direttivo e ispettivo.
Nel pomeriggio di sabato 17 novembre si svolgerà la finale delle Gare di Matematica con le Tecnologie. Bando e regolamento sul sito www.adt.it (Info: [email protected]). Domenica mattina, al termine dei lavori, saranno donati calcolatrici e software, a sorte, solo ai presenti in sala.
Soggiorno
Il Grand Hotel Telese offre la pensione completa, in camera doppia, dalla cena del 16 al pranzo del 18 novembre, quattro coffee-break, inclusa cena di gala: € 190 pp. Supplemento per camera singola: €25. Per i non residenti: un pasto con bevande incluse, € 25; coffee-break standard: € 4; cena di gala: € 50. Il convegnista è invitato a prenotare all’indirizzo [email protected]
La matematica che seduce: video sui frattali
 In questo ‘seducente’ video c’è tutta la bellezza dei frattali, il loro mondo autoripetitivo a ogni livello e altrettanto affascinante a ogni livello.
In questo ‘seducente’ video c’è tutta la bellezza dei frattali, il loro mondo autoripetitivo a ogni livello e altrettanto affascinante a ogni livello.
{wmvremote}http://videolezioni.matematicamente.it/video-media/frattali.wmv{/wmvremote}
Piegamenti
|
|
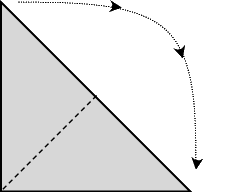
Piegamenti Prendo un foglio grande grande e sottile sottile a forma di triangolo rettangolo isoscele. Inizio a ripiegarlo sovrapponendo i due vertici dell’ipotenusa, in modo da formare un triangolo più piccolo simile al primo. Poi ripeto la stessa operazione, la compio in totale10 volte. Quanti "strati" posso ora contare su ogni lato del triangolino che mi resta in mano? Per strato intendo solo quelle parti di foglio visibili dall’esterno (ad esempio, dopo la prima operazione ve ne saranno 2 2 1) |
| soluzioni |
Fantacalcio
 |
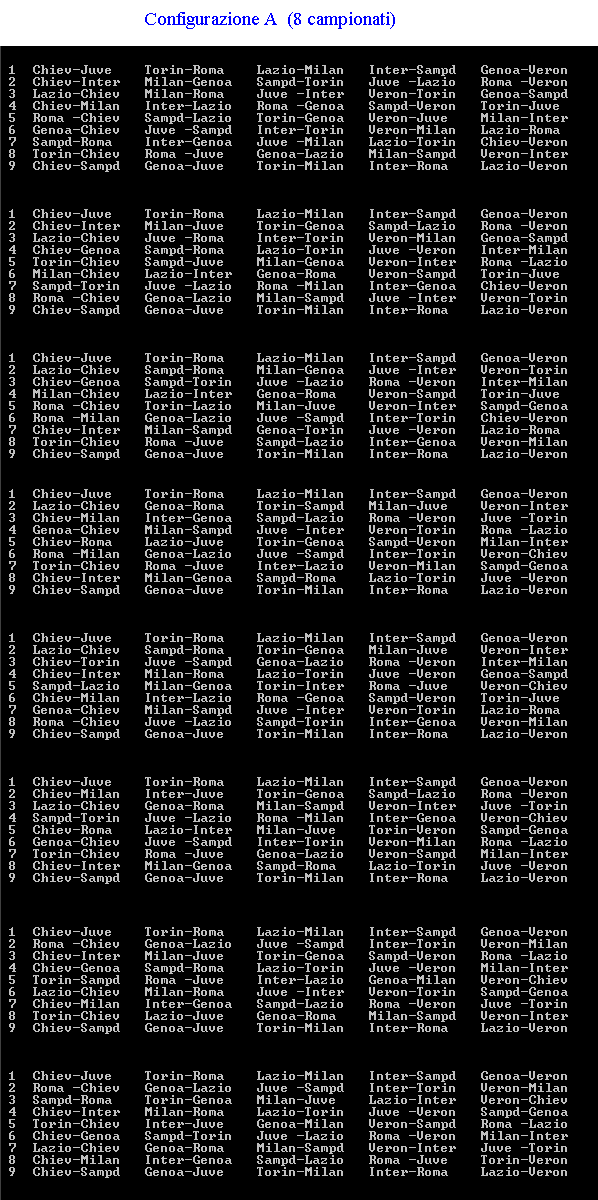
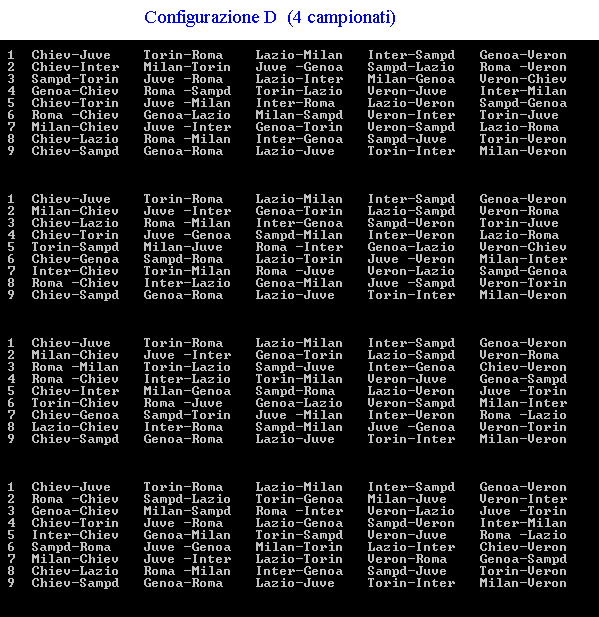
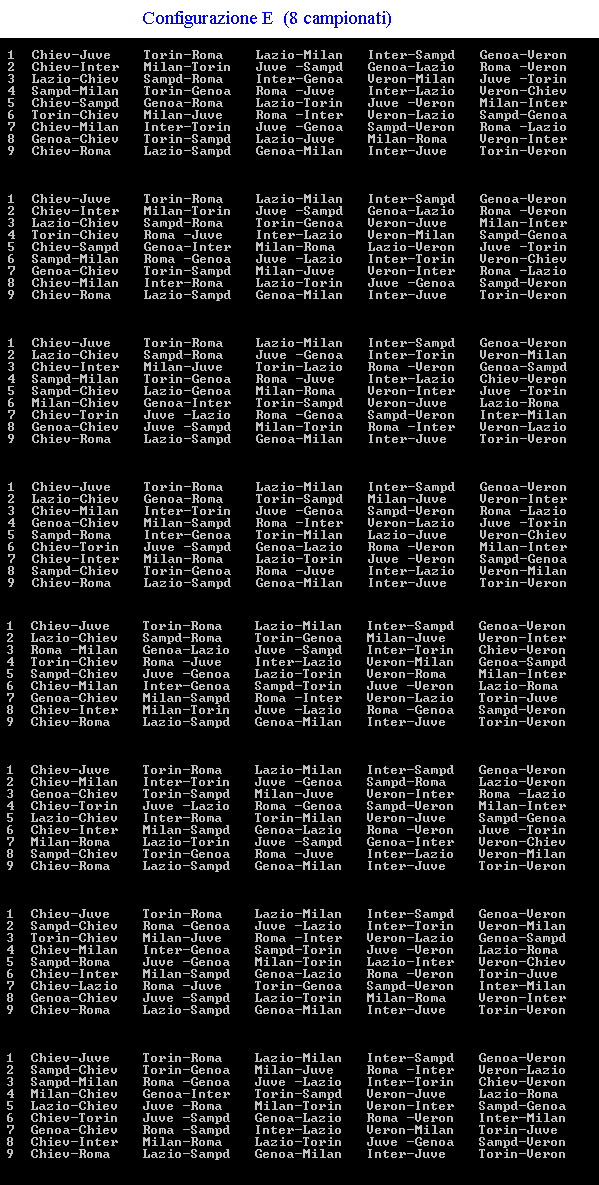
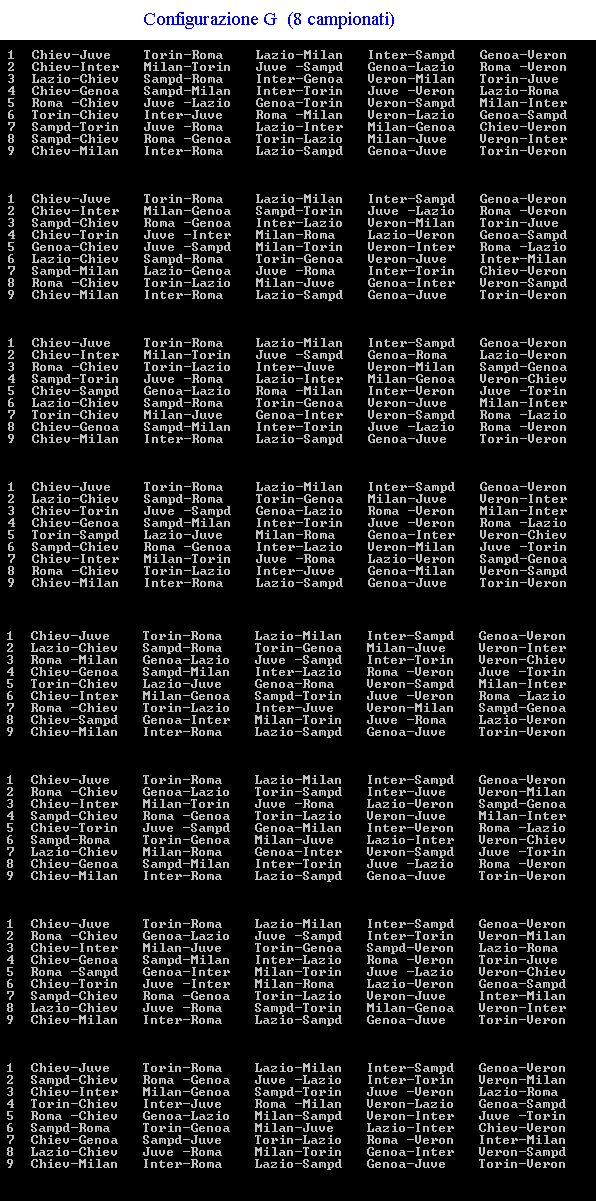
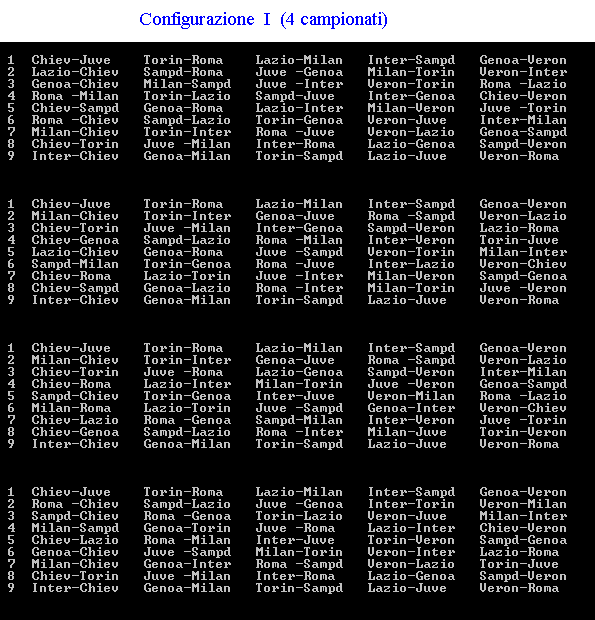
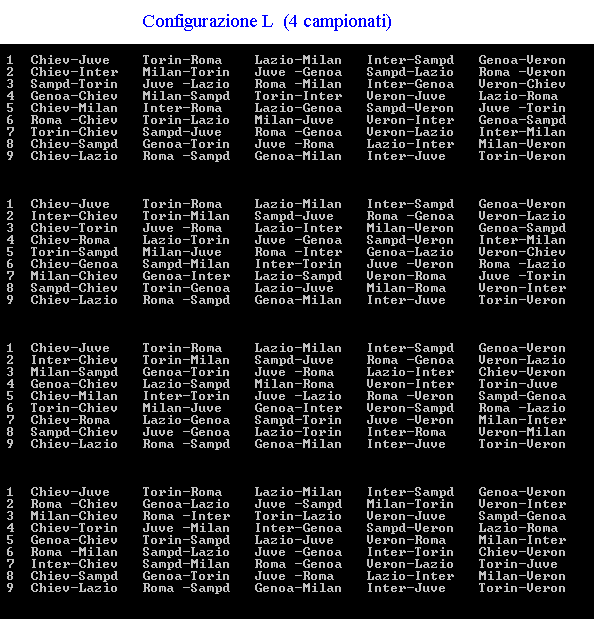
Fantacalcio Se la macchina del tempo ci proiettasse nel futuro, sulle pagine di un giornale sportivo si potrebbe leggere, chissà, la seguente notizia: “Varato tra mille difficoltà il calendario del prossimo campionato di massima serie. Le note vicende della stagione appena conclusa hanno indotto la Federazione Giuoco Calcio ad un drastico ridimensionamento delle società iscritte. Fra dissesti finanziari e retrocessioni per illecito sportivo saranno appena 10 le squadre ai nastri di partenza e soltanto 5 le città che ospiteranno partite della serie A; precisamente: Torino, Genova, Milano, Verona e Roma. Se la prima giornata prevede i seguenti incontri: Per chi non si interessa di calcio si ricordano alcune convenzioni calcistiche. |
|
soluzione di Michele Bortolazzi soluzione di Clelia Rossi l'autore ha trovato 60 possibili campionati |
|




Biliardo 3D
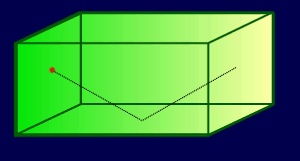 |
Biliardo tridimensionale Il biliardo tridimensionale sarà il gioco del futuro. Durante le lunghe traversate, in assenza di gravità, i crocieristi spaziali giocheranno lanciando piccole sfere in camere a forma di parallelepipedo, le sfere rimbalzeranno sulle pareti del biliardo senza perdere molta energia e riflettendo perfettamente come raggi luminosi, ossia l'angolo di incidenza sarà uguale a quello di riflessione e la retta normale alla parete nel punto dell'urto sarà bisettrice all'angolo formato dalla traiettoria della biglia. In un biliardo a forma di parallelepipedo di dimensioni 3, 4, 5, sarà possibile costruire una traiettoria chiusa che colpendo una dopo l'altra tutte le pareti, senza colpire due volte la stessa parete, ritorni esattamente nel punto di partenza? Descriverne la traiettoria. |
il foglio Excel di Mike
La soluzione di Elena Saccardi
La soluzione di Francesco Vinciprova
La gif animata di Francesco Vinciprova

La soluzione di Jeckyll
L'applet di Jeckyll
Un programma in Visual Basic di Giovanni Schgor
La soluzione di Danilo Mascheroni
Onda verde
|
Onda verde |
|
| Costanza, come tutti gli abitanti di Constown, ogni mattina va a lavorare e, quando prende la macchina, segue la seguente regola: calcola attentamente la situazione di partenza in modo da poter poi arrivare fino a destinazione mantenendo sempre la stessa velocità. La sua abitazione dista 5 km dal suo posto di lavoro e la strada è interrotta da 4 incroci con semaforo alla distanza di 1 km l’uno dall’altro. I semafori di Constown sono estremamente regolari e possono essere solo verdi oppure rossi, anche se caratterizzati da durate diverse. Non spaventatevi però, perché nel paese non si verificano mai incidenti, dato che tutti gli abitanti sono estremamente meticolosi nel calcolare le velocità a cui procedere, ovviamente facendo in modo da non attraversare mai un incrocio nel preciso istante in cui il semaforo cambia di colore. Sulla strada che Costanza deve percorrere, il primo semaforo ha un ciclo di 40 s (rispettivamente 20 s di verde, 20 s di rosso, e così via…), il secondo ha un ciclo di 60 s, il terzo ha un ciclo di 80 s e il quarto ha un ciclo di 100 s. Nell’istante in cui parte da casa, Costanza vede che il primo e il terzo semaforo sono appena diventati rossi, mentre il secondo e il quarto sono appena diventati verdi. Supponendo di trascurare il tempo di accelerazione iniziale della macchina (ovvero immaginando che essa parta già alla velocità desiderata), a quale velocità suggerireste a Costanza di procedere per raggiungere il prima possibile il suo posto di lavoro |
 |
Sondaggio
|
Il sondaggio |
|
| La Matematicamente s.p.a. ha incaricato la società GraDiente s.r.l. di realizzare un sondaggio per capire quali siano le preferenze degli studenti delle scuole superiori nei vari campi della matematica. La GraDiente riferisce che tra gli studenti che studiano analisi matematica, geometria e algebra, il 79% gradisce l’analisi matematica, l'11 % la geometria, il 12 % algebra; mentre al 4 % piace analisi matematica e geometria, al 5 % analisi matematica e algebra, al 2 % algebra e geometria e all'8 % tutte e tre le discipline. Il consiglio di amministrazione della Matematicamente s.p.a., si chiede se i dati presentati dalla GraDiente siano congruenti oppure no. Voi che ne dite? Motivate la risposta.
|
 |
Piove
 Dopo una nuvola passeggera di pioggia, Mario osserva sul suo tavolino circolare le gocce di pioggia cadute. Considerando la distanza radiale delle gocce depositate dal centro del tavolino Mario si chiede: qual è la probabilità che la distanza minima dal centro sia x e che la sola componente radiale della distanza tra questa goccia e quella immediatamente successiva sia y? Si supponga che le gocce, puntiformi, siano cadute uniformemente e indipendentemente sul piano del tavolino e che la densità di pioggia per unità di superficie sia d.
Dopo una nuvola passeggera di pioggia, Mario osserva sul suo tavolino circolare le gocce di pioggia cadute. Considerando la distanza radiale delle gocce depositate dal centro del tavolino Mario si chiede: qual è la probabilità che la distanza minima dal centro sia x e che la sola componente radiale della distanza tra questa goccia e quella immediatamente successiva sia y? Si supponga che le gocce, puntiformi, siano cadute uniformemente e indipendentemente sul piano del tavolino e che la densità di pioggia per unità di superficie sia d.
Torneo di carte

Georges de La Tour, Giocatori di carte , 1619-20
La soluzione di Mamo
La soluzione di Mirco59
La soluzione di Tony
La soluzione di X
Superficie26
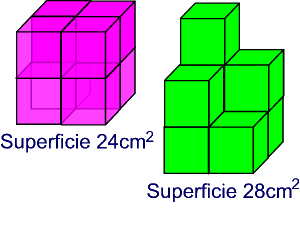 |
Superficie 26 Con otto cubetti di 1cm di lato costruire, se esiste, una figura che abbia la superficie esterna di 26cm2 . Ogni cubetto deve avere almeno una faccia in comune con un altro cubetto. |
| soluzione di jeckyll
altre soluzioni
|
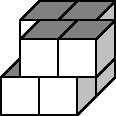 disegno di Giorgio Goldoni
disegno di Giorgio Goldoni
disegno di Luigi Caspani
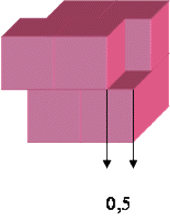 disegno di Elena saccardi
disegno di Elena saccardi
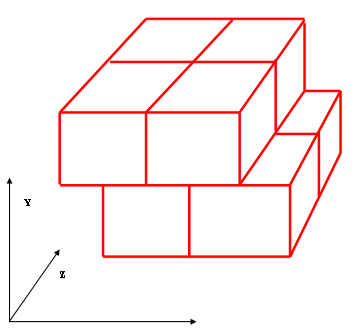 disegno di Mike
disegno di Mike
Tutti questi disegni mostrano dei solidi che rispettano le condizioni chieste dal quesito "Ogni cubetto deve avere almeno una faccia in comune con un altro cubetto". Molti si sono lasciati ingannare da un pregiudizio di cui non sono riusciti a liberarsi e cioè che i cubetti devono avere in comune solo facce intere.
Biglie rotanti
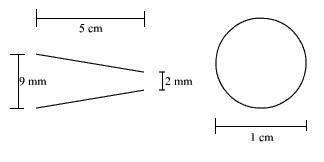 |
Biglie rotanti Antonio ha costruito una pista per le biglie. Questo percorso prevede anche il passaggio su una guida formata da due binari non paralleli come in figura (vista dall’alto). Mentre la biglia percorre questa guida Antonio è in grado di dire quanti giri la biglia compie su se stessa. Lo sapreste dire anche voi? |
| soluzione |
soluzione La biglia compie circa 2,0137 giri
Il quesito non era di facile risoluzione; l'errore più comune è stato quello di non considerare i contributi di rotazione della biglia agli estremi della guida.
Le soluzioni corrette pervenutemi sono:
Jeckyll (Marcello Falco) pdf [179 kB] , animazione java
MaMo (Maurizio Morandi) doc word [66 kB]
mike (Pasquale Salemme) doc word [41 kB] , foglio Excel [15 kB]
tony (Antonio Fuortes) doc word [87 kB]
Torre di Hanoi

Figura 1. La torre di Hanoi
Figura 2. Partenza
Figura 3. Arrivo |
La torre di Hanoi La Torre di Hanoi è un notissimo gioco inventato dal matematico francese Lucas verso la fine dell'800. Si tratta di spostare una torre di 8 dischi di dimensioni variabili da un piolo ad un altro, avendone a disposizione un terzo. Le regole sono poche e semplici: si può spostare un disco per volta e mai un disco più largo deve poggiare su uno più piccolo. |
| soluzioni di Maurizio Morandi e Wonderp |
Rendita
 |
La rendita Un quarantenne ha vinto 200.000 Euro ad una lotteria e vorrebbe garantirsi una rendita annuale indicizzata per i prossimi 25 anni. Esamina le varie proposte di investimento. Quale sarà l’ammontare della prima rata da riscuotere? |
|
|
Insiemi quadrato
 |
Insiemi di un quadrato Si consideri un quadrato, il suo insieme primario definito come quello avente per elementi la misura del suo lato e del raggio del cerchio ad esso circoscritto ed il suo insieme secondario avente per elementi la misura della sua diagonale e del raggio del cerchio inscritto. |
| soluzione
|
Milano percorso
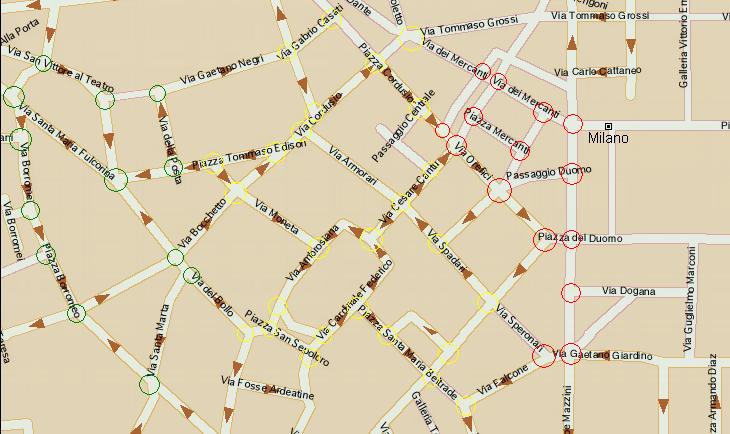 |
Il giro d'Italia a Milano Gli organizzatori del Giro d’Italia stanno transennando alcune vie del centro di Milano per delimitare le zone interessate al percorso ciclistico. Nella cartina riportata a fianco alcuni incroci sono cerchiati in rosso, alcuni in verde e altri in giallo. Gli incroci in rosso sono quelli sicuramente non transitabili dai non addetti ai lavori, quelli verdi sono liberi. |
| soluzione | |
|
|
soluzione Le strade da transennare sono 4, tramutando 11 incroci gialli in verde.
La soluzione di Jeff (Gianluca Busan):
Un primo tentativo, per capire l'ordine del problema, è quello di provare a transennare tutti i gialli in verde o in rosso.
Trasformarli tutti in verde significa transennare 7 strade (e sicuramente tra tutte le transennature di cardinalità 7, questa è la migliore)
Trasformarli tutti in rosso significa transennare 4 strade (e sicuramente tra tutte le transennature di cardinalità 4, questa è la peggiore)
Visto che si è interessati a minimizzare in numero di strade transennate, sicuramente trasformare tutto in rosso è preferibile che trasformare tutto in verde.
Perciò la soluzione del problema sarà un numero minore o uguale a 4. E se fosse 4 bisognerebbe cercare quella transennatura che massimizza gli incroci verdi.
Per risolvere il problema facciamo alcune considerazioni:
1. costruiamo il grafo associato alla cartina: i nodi sono gli incroci e gli archi sono le strade. E' evidente che il grafo è PLANARE (vedi figura 1 in allegato).
2. dalla teoria dei grafi si sa che si può trasformare tale grafo planare nel grafo duale (vedi figura 2 in allegato): tale grafo ha come nodi le regioni di piano comprese tra gli archi del primale (in figura1 tali aree sono etichettate, in figura 2 i nodi hanno le etichette corrispondenti); due nodi del grafo duale sono collegati da un arco se le corrispondenti aree del primale sono confinanti con almeno un lato (arco)
Nel primale, il problema consiste nel transennare delle strade (togliere degli archi) in modo da creare due sottografi separati tali per cui gli incroci verdi stiano su un sottografo e quelli rossi sull'altro. E' evidente dalla figura 1 che si dovrà sicuramente tagliare un arco a nord ed uno a sud (sono i cammini marcati in blu) altrimenti è possibile andare da un incrocio verde ad uno rosso.
Per esempio (vedi figura): transenniamo un arco a nord ed entriamo nell'area N1, adesso entriamo nell'area C8 transennando l'arco di confine tra N1 e C8, allo stesso modo da C8 potremmo passare in C14 e poi in C15, in S3 e transennare un arco blu a sud: a questo punto se nel passare da un'area all'altra transenniamo la strada di confine (tra le aree) il "cammino" N1-C8-C14-C15-S3 "separa" il grafo primale in due sottografi che soddisfano la condizione di separare gli incroci verdi da quelli rossi. Gli incroci gialli della componente connessa di sinistra diventano verdi quelli di destra rossi. In questo esempio la transennatura ha cardinalità 6 (1 + NUMERO DI NODI NEL CAMMINO N1-C8-C14-C15-S3 ).
E' evidente che "N1-C8-C14-C15-S3" è un cammino ammissibile nel grafo duale (figura 2). Rendere minima la cardinalità della transennatura significa cercare un cammino minimo sul grafo duale.
Per risolvere il problema si deve sicuramente "entrare" in una regione a nord (N1 o N2 o N3) ed "uscire" da una regione a sud (S1, S2, S3, S4, S5) [tali regioni sono quelle che hanno almeno un lato colorato di blu]
Risolvere il problema significa quindi cercare un cammino minimo tra un nodo di tipo Nx ed uno di tipo Sy. Un tale cammino determina una (o più, per esempio se il nodo finale fosse S2, ci sarebbero 3 possibili strade da transennare) sezione del grafo primale in modo da soddisfare la condizione di dividere gli incroci verdi da quelli rossi. A parità di cammino minimo si deve preferire quello che nell'equivalente primale massimizza gli incroci verdi.
In letteratura esistono parecchi algoritmi di cammino minimo: per esempio con l'algoritmo di Bellman-Ford si possono trovare tutti i cammini minimi, per usarlo basta aggiungere un nodo sorgente S e collegarlo ai nodi Nx ed aggiungere un nodo target T e collegarlo con i nodi di tipo Sy; inoltre basta dare peso 1 a tutti gli archi. A questo punto tutti i cammini minimi tra S e T sono anche cammini minimi per il duale e quindi soluzioni probabili per il primale.
Una volta trovati tutti i cammini minimi, si torna al primale e si applicano i tagli, si contano gli incroci gialli da trasformare in verde e si sceglie il "cammino" che massimizza tale numero.
Nel nostro esempio (vedi figura 2) il cammino minimo è lungo 2 (è un grafo talmente semplice che si vede ad occhio: non ci sono archi diretti (cammino lungo 1) tra un Nx e un Sy, però ne esiste almeno uno di lunghezza 2 (N1-C5-S1), perciò il minimo è 2).
Tutti i cammini di lunghezza 2 sono i seguenti:
N1-C5-S1
N1-C7-S1
N1-C7-S2
N1-C7-S3
Tra questi quello che massimizza gli incroci verdi è N1-C7-S3 a cui corrisponde un unico "taglio" del primale (vedi figura 3). Si vede da tale figura che le transenne da mettere sono 4 e che gli incroci gialli trasformati in verde sono 11.
La figura 4 mostra il taglio direttamente sulla cartina originale.
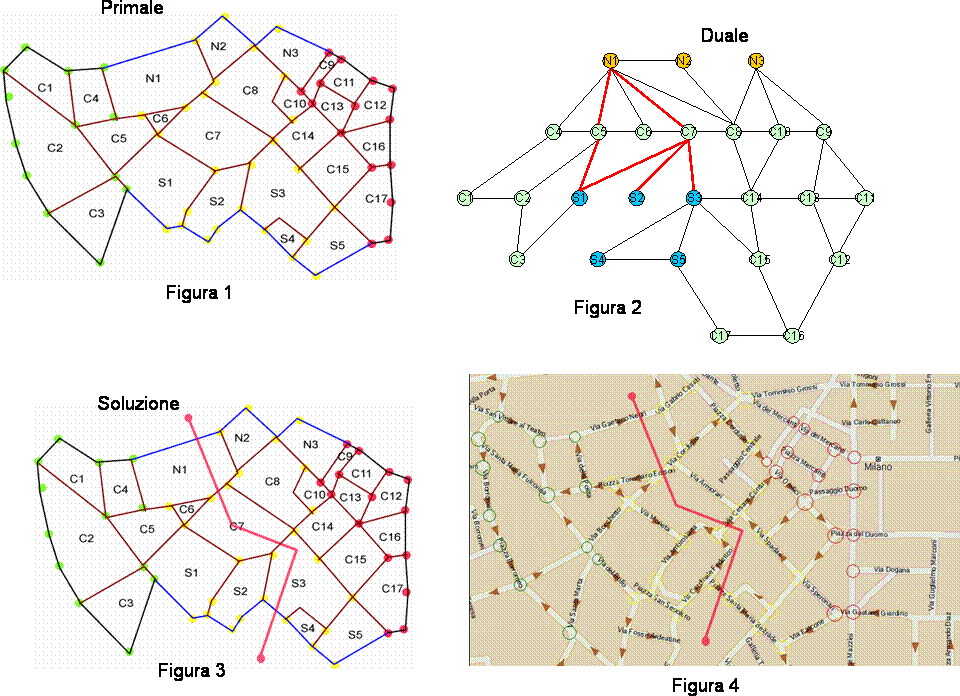
La soluzione di Luca Barletta:
Il quesito si può interpretare nel seguente modo: stiamo cercando un taglio di cardinalità minima su un grafo ciclico non orientato. Un taglio è una partizione del grafo (=la nostra rete stradale) in due componenti connesse, vale a dire due sottografi di n e m nodi (=incroci della rete), con n+m numero totale di nodi del grafo originario; connesse nel senso che in ogni sottografo un nodo è collegato almeno ad un altro del sottografo stesso. L'insieme del taglio ha come elementi gli archi (=strade) che, se tolti, determinano la partizione del grafo.
Cercare un taglio di cardinalità minima del grafo equivale a trovare il flusso massimo sullo stesso grafo: infatti il taglio minimo può essere visto come un "collo di bottiglia" che limita il flusso di una quantità, questo flusso è massimo per il grafo.
Premesso ciò, il quesito poteva essere risolto in 12 passaggi, alcuni dei quali ripetitivi.
- sostituiamo tutti gli incroci verdi con un unico nodo verde e analogamente per gli incroci rossi
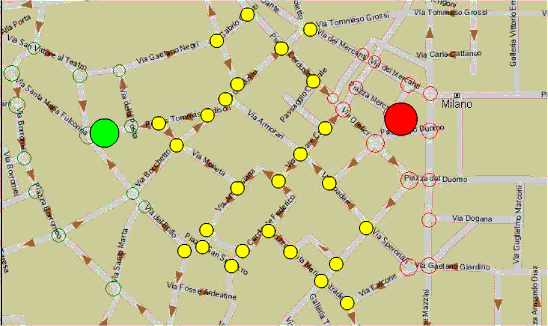
- aggiungiamo tutti gli archi del grafo assicurandoci di collegare correttamente i nodi gialli ai nodi rosso e verde
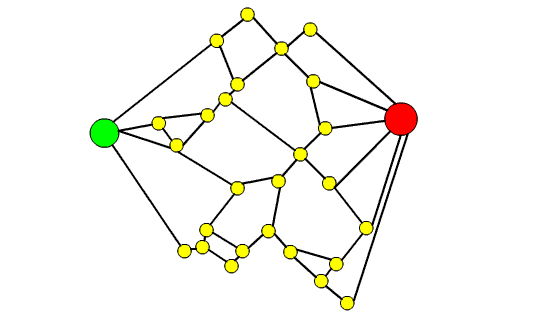
- dobbiamo trovare il flusso massimo: cominciamo a spedire la prima unità di flusso sul grafo su un cammino che vada dal nodo verde al nodo rosso (il cammino deve avere il minor numero di archi possibile)
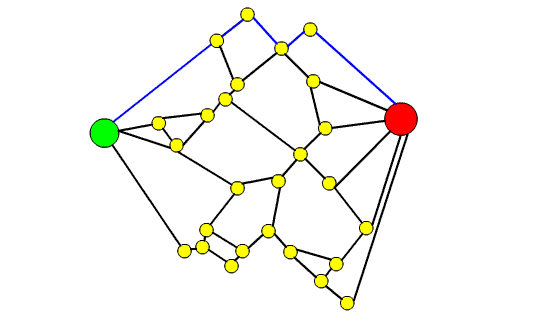
- poichè ogni arco ha capacità unitaria (può essere trasportata solo un'unità di flusso sugli archi), gli archi del cammino minimo trovato precedentemente non sono più utilizzabili; pertanto porremo una freccia su ogni arco del cammino; la freccia è concorde con la direzione verde-rosso del cammino
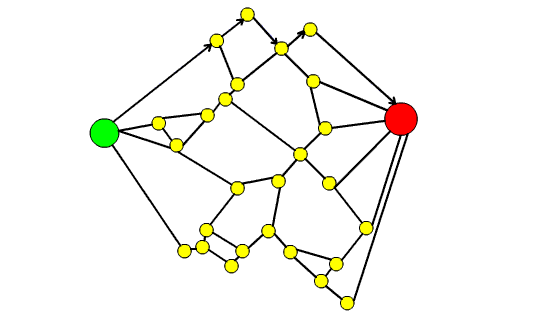
- troviamo il secondo cammino minimo
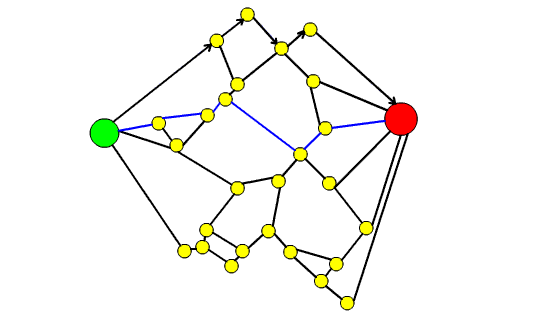
- per le stesse ragioni espresse nel punto 4 procediamo col porre le frecce
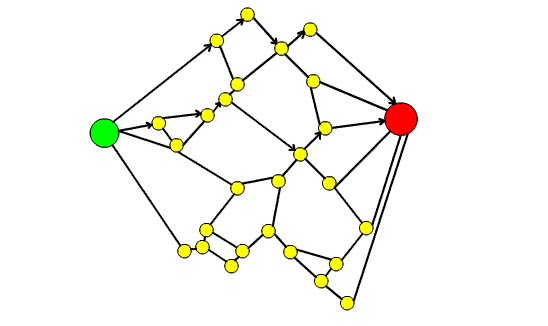
- troviamo il terzo cammino minimo
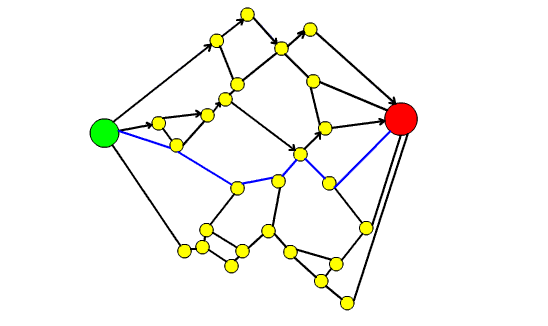
- per le stesse ragioni espresse nel punto 4 procediamo col porre le frecce
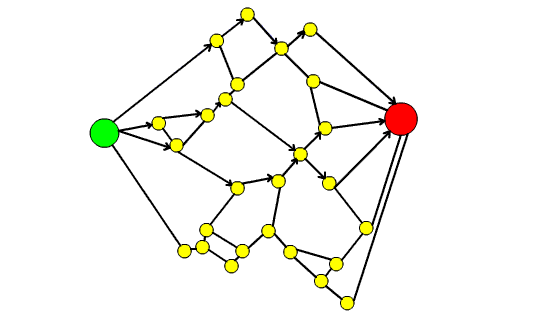
- troviamo il quarto cammino minimo
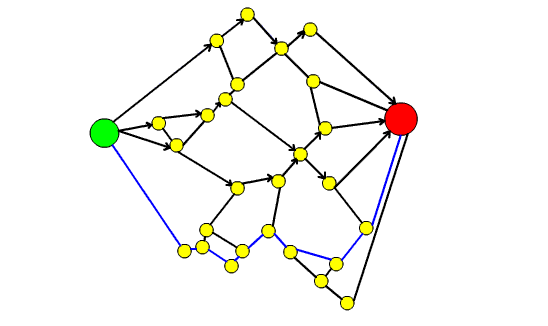
- per le stesse ragioni espresse nel punto 4 procediamo col porre le frecce
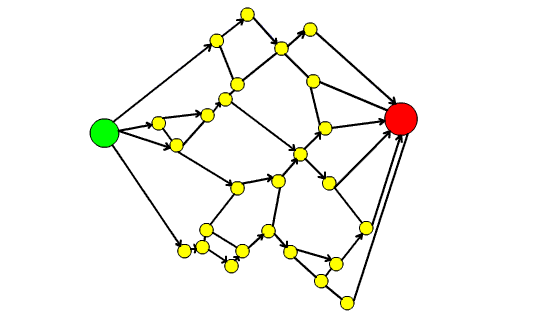
- ci accorgiamo che non possiamo più trovare cammini minimi. Esiste un teorema che dice che in un grafo o esiste un cammino che collega il nodo s al nodo t oppure esiste un taglio che partiziona i nodi in due insiemi A e B e tale che s appartiene ad A e t appartiene a B.
Noi siamo giunti alla seconda condizione, abbiamo trovato un taglio perchè non ci sono più cammini minimi; l'insieme degli archi che formano il taglio saranno le strade che verranno transennate.
Per individuare gli archi del taglio facciamo partire un'unità di flusso dal nodo rosso e percorriamo tutti gli archi percorribili, tenendo conto che gli archi senza freccia sono bidirezionali, mentre rispettiamo la direzione degli archi orientati (gli archi percorribili sono evidenziati in rosa e gli archi appartenenti al taglio indicati con la lettera B)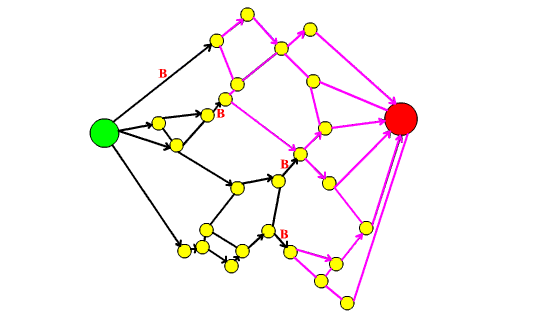
- a questo punto possiamo assegnare il colore definitivo agli incroci gialli (verde o rosso)
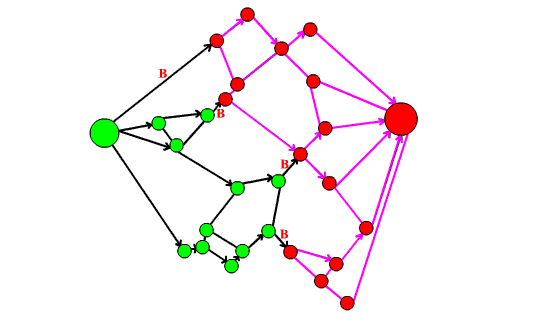

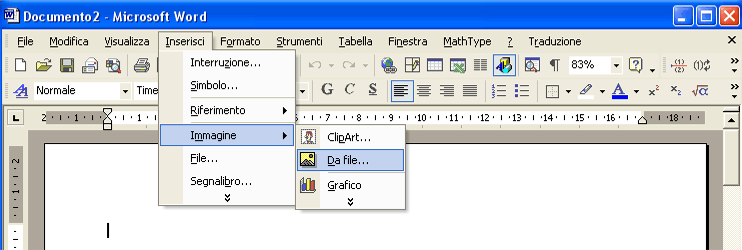
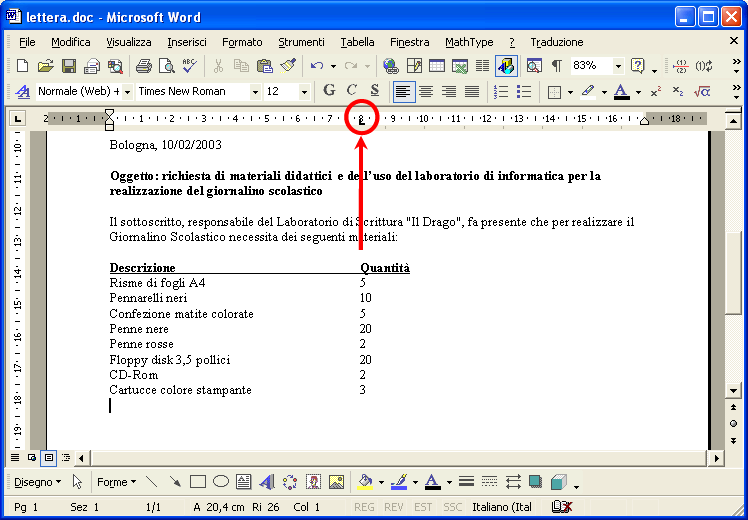
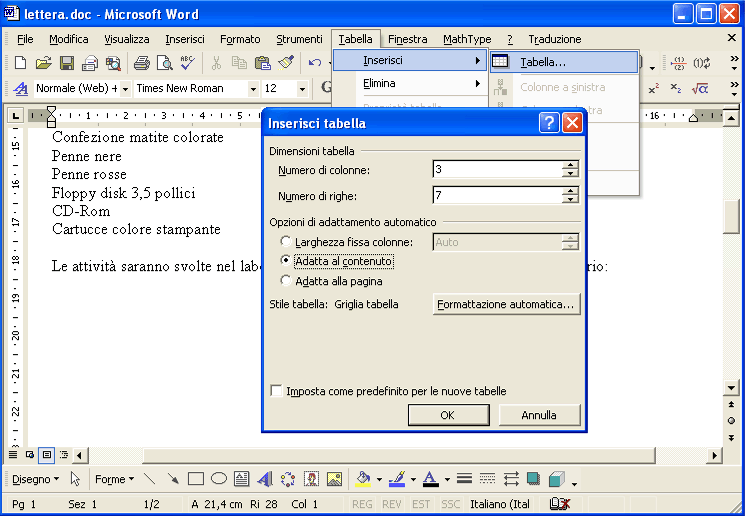
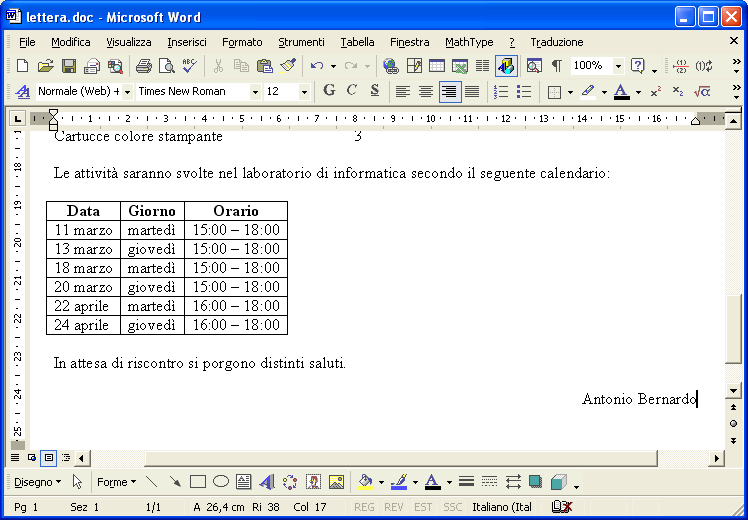
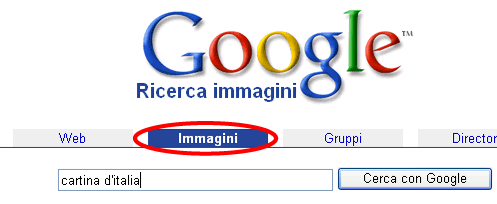
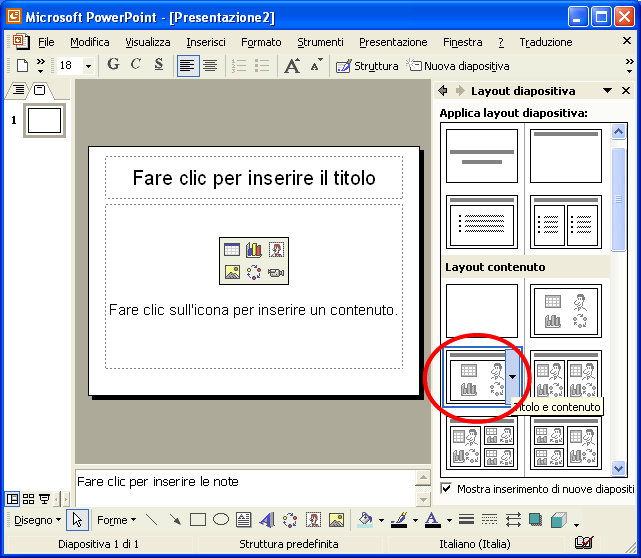
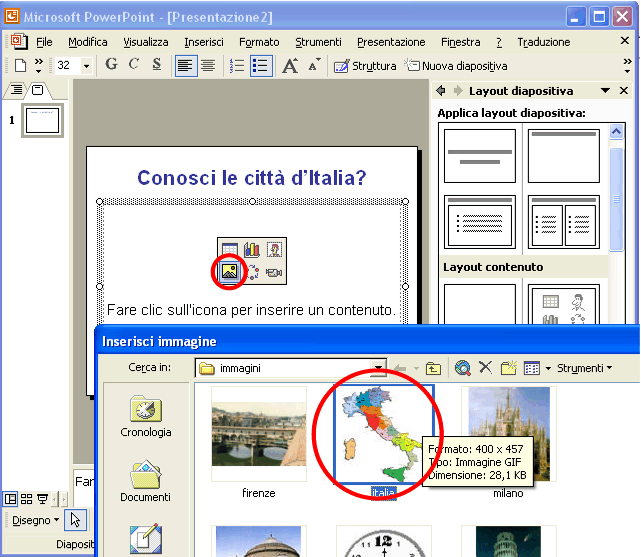
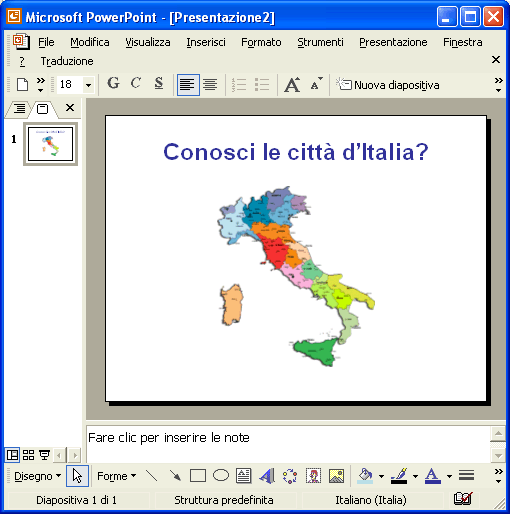
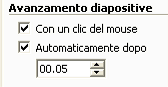
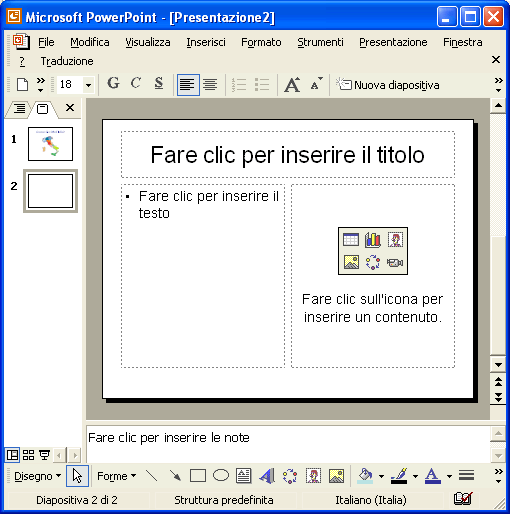
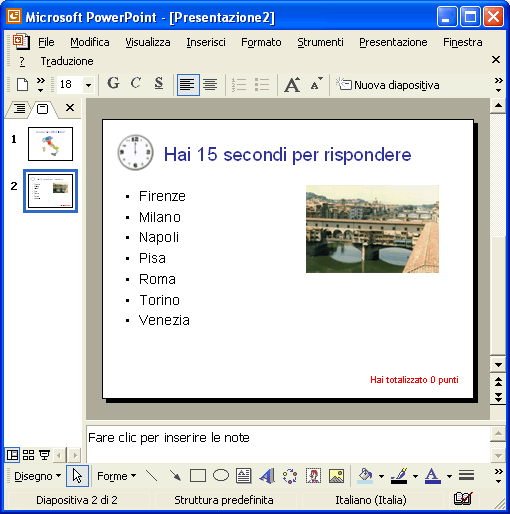
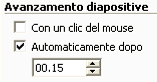
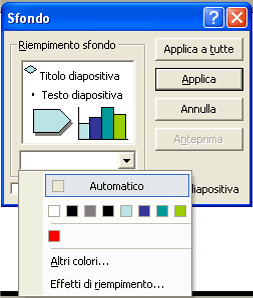
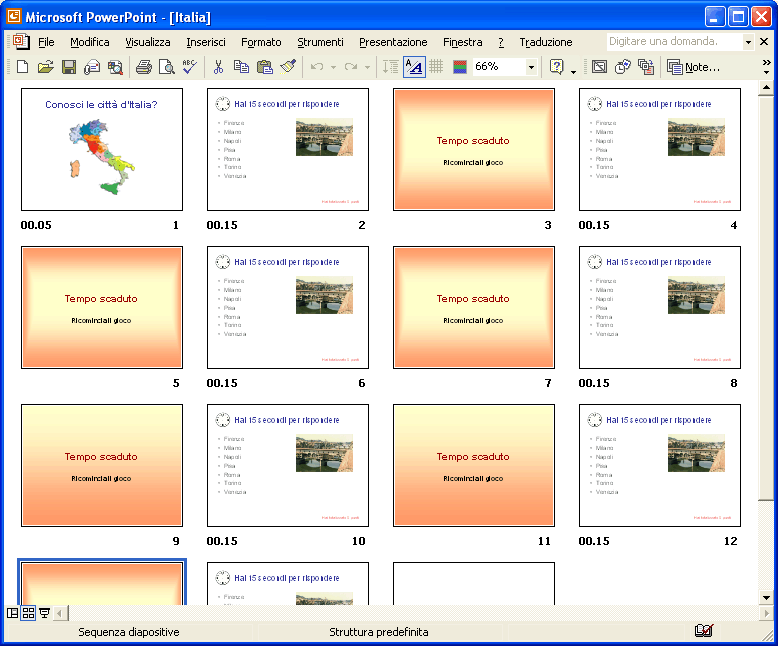
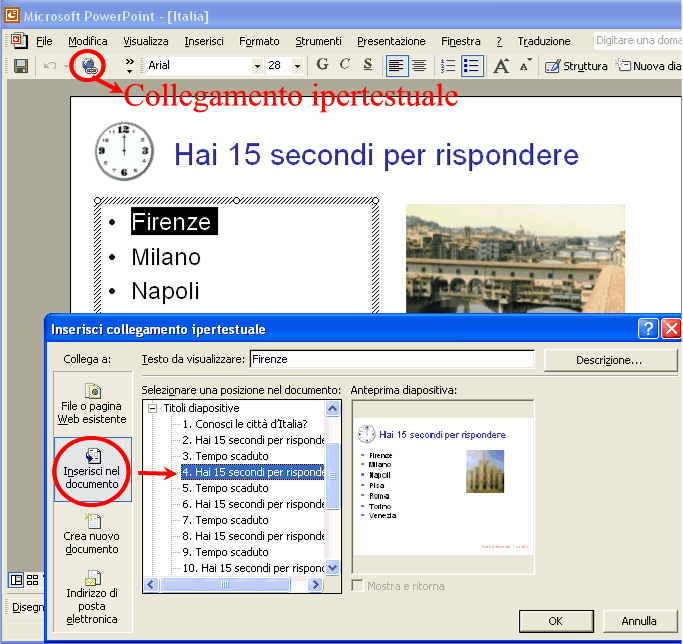
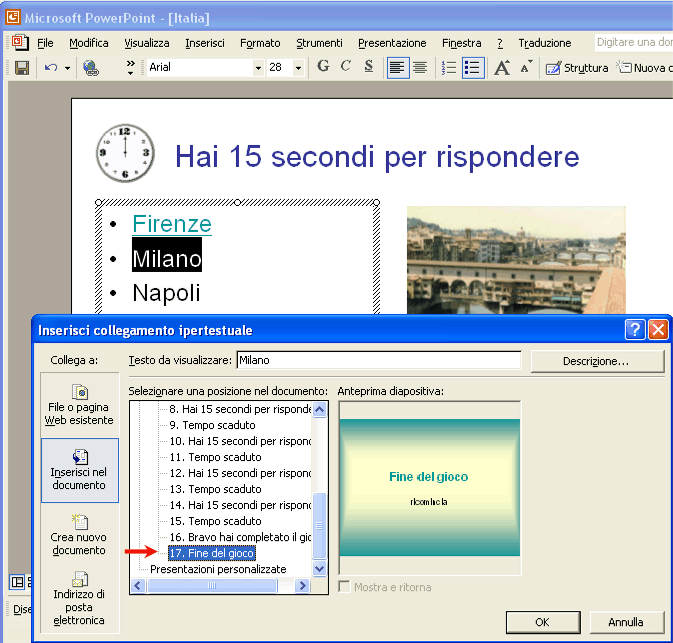
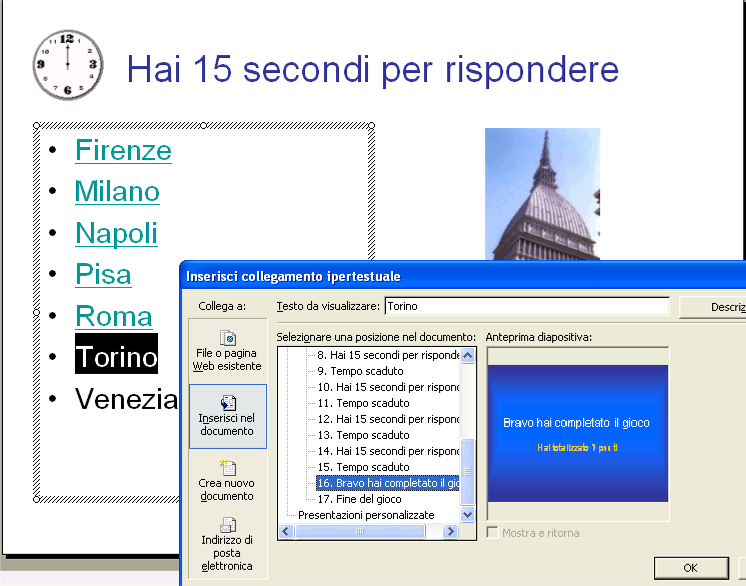
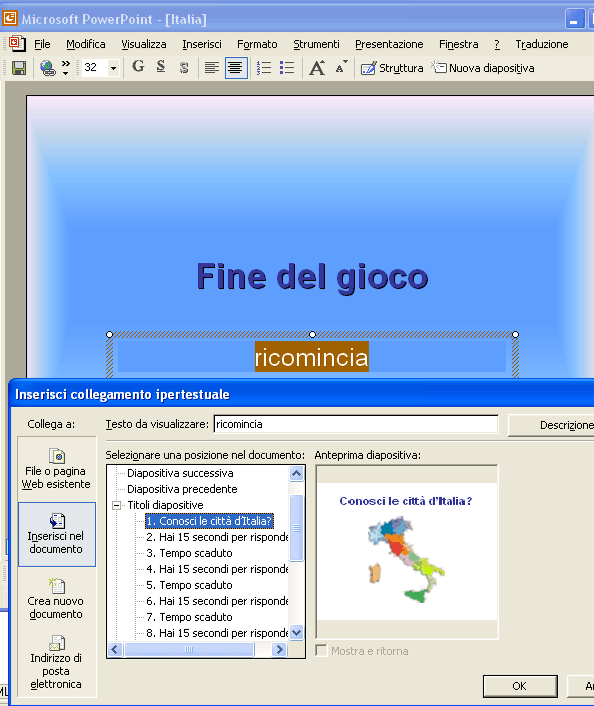
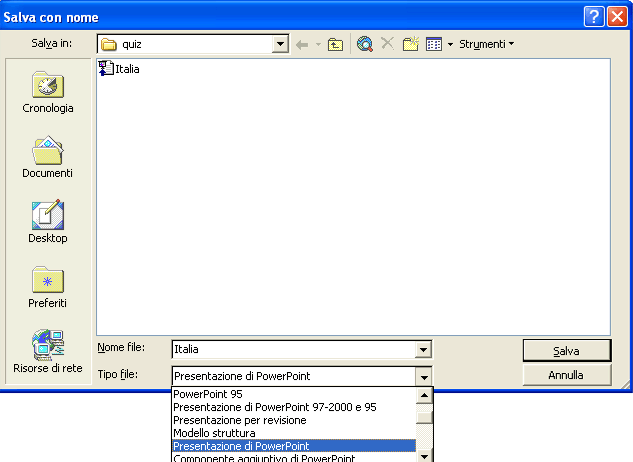

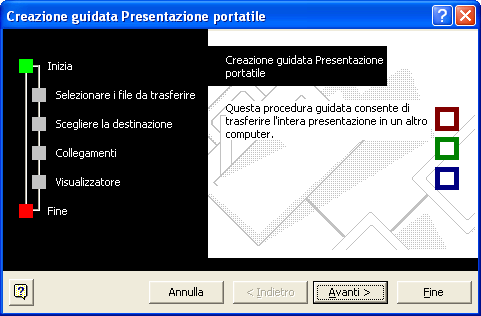

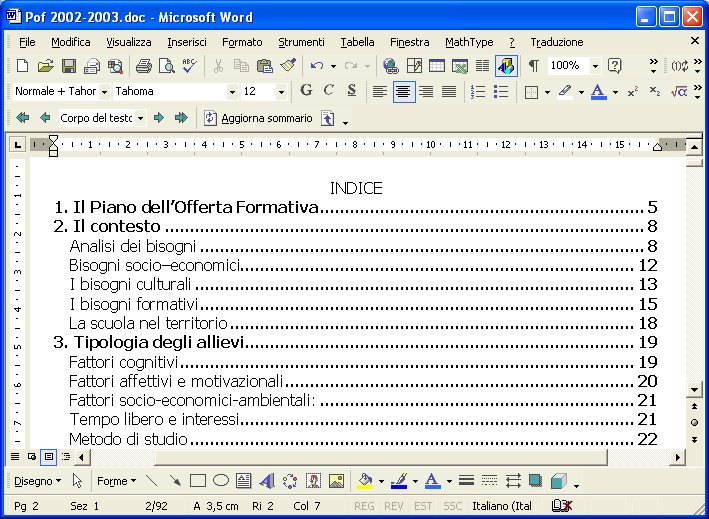
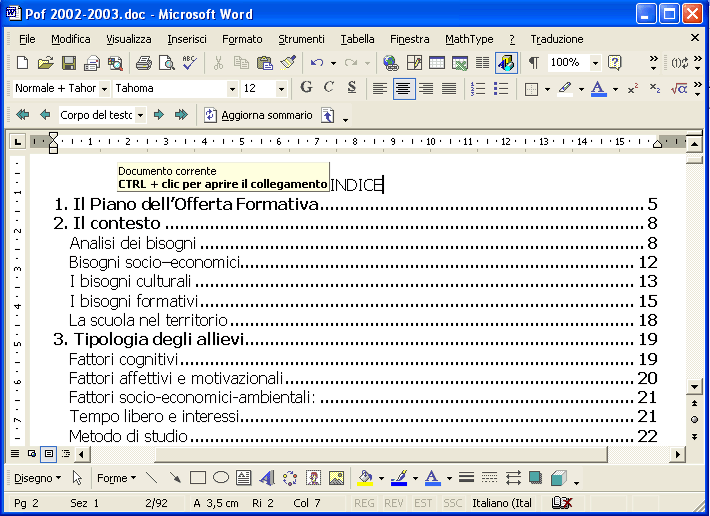
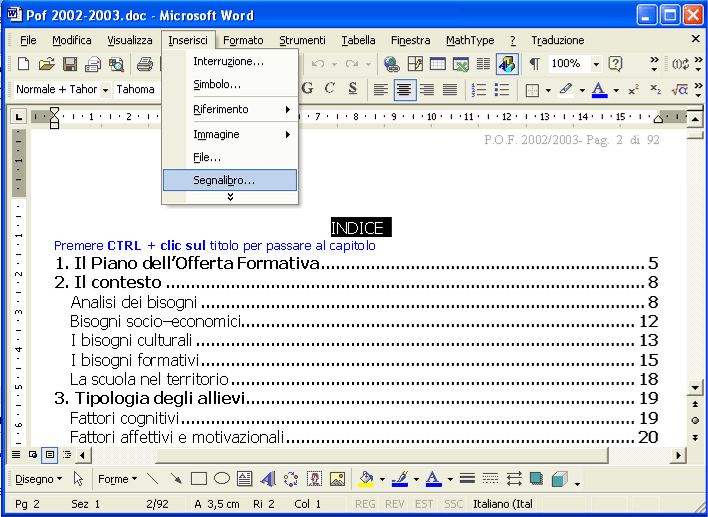
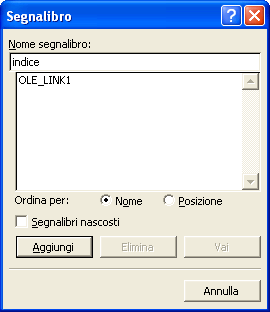
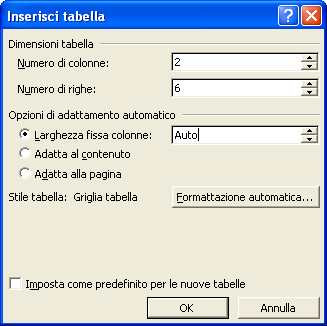
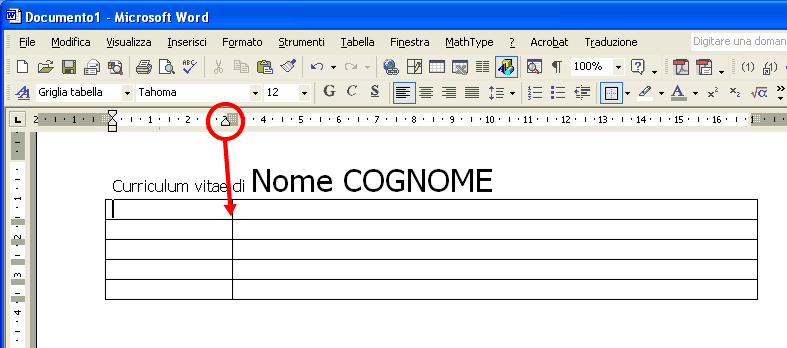
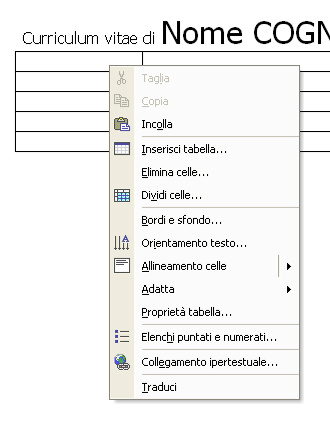
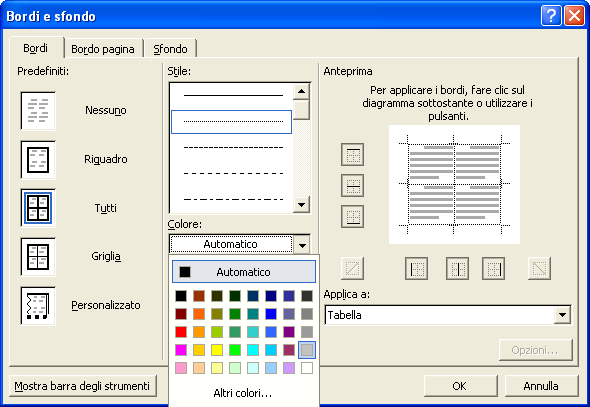
 .
.