Nella famiglia F di circonferenze di equazione:
$2 x^2 + 2 y^2 + 2ax + 2by + 4a + 3b = 0 $
determinare quella il cui centro C appartiene alla bisettrice del 1°e del 3° quadrante e che passa per $P(1;-2)$ e l’area e il perimetro del quadrilatero convesso ottenuto congiungendo i punti di intersezione della circonferenza con gli assi coordinati.
Determinare inoltre:
- l’equazione della parabola avente il vertice V sull’asse y e passante per P e C;
- sull’arco di parabola situato nel 4° quadrante un punto S in modo che risulti: $ \bar {SH} + \bar{SK} = \bar{CP}$ , essendo $ \bar {SH}$ e $ \bar {SK}$ le distanze di S dagli assi x e y.
Risoluzione (0)
Sapendo che il centro della circonferenza appartiene alla bisettrice del 1° e del 3° quadrante, cioè a $ y = x$ , sappiamo che le sue coordinate sono uguali.
Possiamo quindi scrivere che:
$ C ( – a/2 ; – a/2 )$
Poiché $ – a/2 = – b/2$ , possiamo affermare che a=b. In questo caso l’equazione della circonferenza diventa:
$ 2x^2 + 2y^2 + 2ax + 2ay + 4a + 3a = 0 $
$2 x^2 + 2 y^2 + 2ax + 2ay + 7a = 0 $
Dividiamo tutto per 2:
$ x^2 + y^2 + ax + ay + 7/2 a = 0 $
Determiniamo ora il valore del raggio utilizzando la formula $ r = sqrt((a/2)^2 + (b/2)^2 – c ) $ , che nel nostro caso diventa:
$ r = sqrt((a/2)^2 + (a/2)^2 – c ) = sqrt(2 (a/2)^2 – c ) = sqrt(2 * (a^4)/4 – c ) = sqrt((a^2)/2 – c ) $
Sappiamo che la circonferenza passa per il punto P di coordinate (1;-2) e abbiamo le coordinate del suo centro $ C ( – a/2 ; – a/2 )$ .
Possiamo trovare quindi il suo raggio calcolando la distanza fra i punti C e P:
$ CP = sqrt((x_1 – x_2)^2 + (y_1 – y_2)^2) = sqrt((1 + a/2)^2 + (-2 + a/2)^2) = $
$ sqrt(1 + (a^2)/4 + a + 4 + (a^2)/4 – 2a) = sqrt( (a^2)/2 – a + 5 ) $
Possiamo ora eguagliare i due valori del raggio trovati:
$ sqrt( (a^2)/2 – c ) = sqrt( (a^2)/2 – a + 5 ) $
Eleviamo tutto al quadrato e risolviamo l’equazione:
$ (a^2)/2 – c = (a^2)/2 – a + 5 $
$ – c = – a + 5 to a – c = 5 $
Considerando l’equazione della circonferenza $ x^2 + y^2 + ax + ay + 7/2 a = 0 $ , sappiamo che $ c = 7/2 a$ , quindi:
$ a – 7/2 a = 5 to 2a – 7a = 10 to a = -2 $
Di conseguenza sappiamo che $ b = a = – 2$ e che $ c = 7/2 a = 7/2 * (-2) = – 7 $ ; l’equazione della circonferenza è quindi:
$ x^2 + y^2 – 2x – 2y – 7 = 0 $
Rappresentiamo la circonferenza nel piano cartesiano, sapendo che il suo centro è in C(1;1) e che il suo raggio misura 3:

Troviamo ora i suoi punti di intersezione con gli assi; cominciamo trovando l’intersezione con l’asse y:
$ C ∩ x = 0 $
$$
\left\{ \begin{array}{rl}
x = 0 &\\
x^2 + y^2 – 2x – 2y – 7 = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
x = 0 &\\
y^2 – 2y – 7 = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
x = 0 &\\
y = \frac{1 ± \sqrt{1 + 7}}{2} = \frac{1 ± \sqrt(8)}{2} = \frac{1 ± 2\sqrt(2)}{2} &
\end{array}\right.
$$
Abbiamo quindi due punti, che chiamiamo A e B:
$ A ( 0 ; 1 + 2sqrt2 ) , B ( 0 ; 1 – 2sqrt2 ) $
Determiniamo ora le intersezioni con l’asse x:
$ C ∩ y = 0 $
$$
\left\{ \begin{array}{rl}
y = 0 &\\
x^2 + y^2 – 2x – 2y – 7 = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
y = 0 &\\
x^2 – 2x – 7 = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
x = 0 &\\
x = \frac{1 ± \sqrt{1 + 7}}{2} = \frac{1 ± \sqrt(8)}{2} = \frac{1 ± 2\sqrt(2)}{2} &
\end{array}\right.
$$
Chiamiamo gli altri due punti D ed E:
$ A ( 1 + 2sqrt2 ; 0 ) , B (1 – 2sqrt2 ; 0 ) $
Congiungiamo i punti:
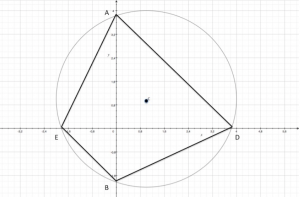
Troviamo il perimetro del quadrilatero formatosi calcolando la distanza fra i punti A e D, D e B, B ed E, E ed A mediante la formula:
$ d = sqrt((x_1 – x_2)^2 + (y_1 – y_2)^2) $
$ \bar{AC} = sqrt((0 – 1 – 2sqrt2)^2 + (1 + 2sqrt2 – 0)^2) = sqrt((- 1 – 2sqrt2)^2 + (1 + 2sqrt2)^2) = $
$ sqrt(1 + 8 + 4sqrt2 + 1 + 8 + 4sqrt2) = sqrt(18 + 8sqrt2) $
Possiamo scomporre il risultato considerando che esso è un radicale doppio:
$ sqrt(a + sqrt(b)) = sqrt(frac(a + sqrt(a^2 – b^2))(2)) + sqrt(frac(a – sqrt(a^2 – b^2))(2))$
$ sqrt(18 + sqrt(128)) = sqrt(frac(18 + sqrt(18^2 – (sqrt(128))^2))(2)) + sqrt(frac(18 – sqrt(18^2 – (sqrt(128))^2))(2)) = $
$ sqrt(frac(18 + sqrt(324 – 128))(2)) + sqrt(frac(18 – sqrt(324 – 128))(2)) = $
$ sqrt(frac(18 + sqrt(196))(2)) + sqrt(frac(18 – sqrt(196))(2)) = sqrt(frac(18 + 14)(2)) + sqrt(frac(18 – 14)(2)) = $
$ sqrt((32)/2) + sqrt(4/2) = sqrt(16) + sqrt2 = 4 + sqrt2 $
Passiamo ora alla distanza DB:
$ \bar{DB} = sqrt((0 – 1 – 2sqrt2)^2 + (1 – 2sqrt2 – 0)^2) = sqrt((- 1 – 2sqrt2)^2 + (1 – 2sqrt2)^2) = $
$ sqrt(1 + 8 + 4sqrt2 + 1 + 8 – 4sqrt2) = sqrt(18) = 3 sqrt2 $
Calcoliamo BE:
$ \bar{BE} = sqrt((0 – 1 + 2sqrt2)^2 + (1 – 2sqrt2 – 0)^2) = sqrt((- 1 + 2sqrt2)^2 + (1 – 2sqrt2)^2) = $
$ sqrt(1 + 8 – 4sqrt2 + 1 + 8 – 4sqrt2) = sqrt(18 – 8sqrt2) $
Come prima, scomponiamo il radicale doppio:
$ sqrt(a – sqrt(b)) = sqrt(frac(a + sqrt(a^2 – b^2))(2)) – sqrt(frac(a – sqrt(a^2 – b^2))(2))$
$ sqrt(18 – sqrt(128)) = sqrt(frac(18 + sqrt(18^2 – (sqrt(128))^2))(2)) – sqrt(frac(18 – sqrt(18^2 – (sqrt(128))^2))(2)) = $
$ sqrt(frac(18 + sqrt(324 – 128))(2)) – sqrt(frac(18 – sqrt(324 – 128))(2)) = $
$ sqrt(frac(18 + sqrt(196))(2)) – sqrt(frac(18 – sqrt(196))(2)) = sqrt(frac(18 + 14)(2)) – sqrt(frac(18 – 14)(2)) = $
$ sqrt((32)/2) – sqrt(4/2) = sqrt(16) – sqrt2 = 4 – sqrt2 $
Infine calcoliamo EA:
$ \bar{EA} = sqrt((0 – 1 + 2sqrt2)^2 + (1 + 2sqrt2 – 0)^2) = sqrt((- 1 + 2sqrt2)^2 + (1 + 2sqrt2)^2) = $
$ sqrt(1 + 8 – 4sqrt2 + 1 + 8 + 4sqrt2) = sqrt(18) = 3 sqrt2 $
Notiamo quindi che due dei lati del quadrilatero sono uguali, in particolare $ \bar{EA} = \bar{DB} $ ; verifichiamo che $ \bar{AD} /// \bar{EB} $ calcolando i coefficienti angolari delle due rette:
$ m = frac(y_2 – y_1)(x_2 – x_1)$
$ m_(AD) = frac(0 – 1 – 2sqrt2)(1 + 2sqrt2 – 0) = frac (- 1 – 2sqrt2)(1 + 2sqrt2) = $
$ – frac(+ 1 + 2sqrt2)(1 + 2sqrt2) = -1 $
$ m_(AD) = frac(0 – 1 + 2sqrt2)(1 – 2sqrt2 – 0) = frac (- 1 + 2sqrt2)(1 – 2sqrt2) = $
$ – frac(+ 1 – 2sqrt2)(1 – 2sqrt2) = -1 $
Possiamo affermare, quindi, che il quadrilatero in questione è un trapezio isoscele.
Determiniamo il suo perimetro:
$ P = \bar{AD} + \bar{DB} + \bar{BE} + \bar{EA} = 4 + sqrt2 + 3sqrt2 + 4 – sqrt2 + 3sqrt2 = 8 + 6sqrt2 $
Per calcolare la sua area dobbiamo conoscere la sua altezza, cioè la distanza del punto B dalla retta AD.
Troviamo l’equazione della retta AD:
$ AD: frac(x – x_1)(x_2 – x_1) = frac(y – y_1)(y_2 – y_1)$
$ AD: frac(x – 0)(1 + 2sqrt2 – 0) = frac(y – 1 – 2sqrt2)(0 – 1 – 2sqrt2)$
$ AD: frac(x)(1 + 2sqrt2) = frac( – y + 1 + 2sqrt2)(1 + 2sqrt2)$
$ AD : x = – y + 1 + 2sqrt2 to AD : x + y – 1 – 2sqrt2 = 0 $
Calcoliamo la distanza del punto $ B ( 0 ; 1 – 2sqrt2) $ dalla retta AD:
$ d = frac(| ax_0 + by_0 + c |)(sqrt(a^2 + b^2))$
$ d(b ; AD) = frac(| 1 * 0 + 1 * (1 – 2sqrt2) – 1 -2sqrt2 |)(sqrt(1^2 + 1^2)) = $
$ frac(| 1 – 2sqrt2 – 1 -2sqrt2 |)(sqrt(1^2 + 1^2)) = frac(| -4 sqrt2 |)(sqrt2) = frac(4 sqrt2)(sqrt2)= 4 $
Sapendo che l’altezza del trapezio vale 4, possiamo calcolare la sua area:
$ A = frac(\bar{AD} + \bar{EB})(2) * h = = frac(4 + sqrt2 + 4 – sqrt2)(2) * 4 = 8/2 * 4 = 4 * 4 = 16 $
Risoluzione (1)
Sappiamo che a parabola passa per i punti C e P; possiamo quindi escludere che il suo asse sia parallelo all’asse y.
La sua equazione sarà quindi:
$ x = ay^2 + by + c $
e il suo vertice di coordinate $ (- frac(Δ)(4a) ; – b/(2a)) $
Imponiamo quindi il passaggio per i due punti:
$ C (1 ; 1) to 1 = a + b + c $
$ P (1 ; -2) to 1 = 4a – 2b + c $
Poiché il vertice della parabola appartiene all’asse y, sappiamo che $- frac(Δ)(4a) = 0$, quindi :
$ – frac(b^2 – 4ac = 0)(4a) = 0 to b^2 – 4ac = 0 $
Mettiamo a sistema le tre scritture:
$$
\left\{
\begin{array}{ll}
a + b + c = 1 & \\
4a – 2b + c = 1 & \\
b^2 – 4ac = 0 &
\end{array}
\right.
$$
Risolviamo per sottrazione le prime due equazioni:
$a + b + c = 1$
$-4a + 2b – c = – 1$
$__________$
$-3a + 3b = 0 to – a + b = 0 to a = b $
Sostituiamo questa uguaglianza ad una delle prime equazioni e alla terza:
$$
\left\{ \begin{array}{rl}
a + a + c = 1 &\\
a^2 – 4ac = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
2a + c = 1 &\\
a^2 – 4ac = 0&
\end{array}\right.
$$
Ricaviamo C dalla prima equazione e risolviamo per sostituzione:
$$
\left\{ \begin{array}{rl}
c = 1 – 2a &\\
a^2 – 4ac = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
c = 1 – 2a &\\
a^2 – 4a (1 – 2a) = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
c = 1 – 2a &\\
a^2 – 4a + 8 a^2 = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
c = 1 – 2a &\\
9 a^2 – 4a = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
c = 1 – 2a &\\
a ( 9a – 4) = 0&
\end{array}\right.
$$
$$
\left\{ \begin{array}{rl}
c = 1 – 2a &\\
a = 0 ∨ a = \frac{4}{9} &
\end{array}\right.
$$
Dobbiamo escludere il caso in cui a sia uguale a zero, altrimenti l’equazione non rappresenterebbe una parabola;
$$
\left\{ \begin{array}{rl}
c = 1 – 2 * 4/9 = 1/9 &\\
a = \frac{4}{9} , b = \frac{4}{9} &
\end{array}\right.
$$
Possiamo scrivere l’equazione della parabola:
$ x = 4/9 y^2 + 4/9 y + 1/9 $
Rappresentiamo la parabola sul piano cartesiano tenendo presente che il suo vertice è di coordinate
$ V ( 0 ; – b/(2a)) $ , cioè $ V (0 ; – 1/2) $
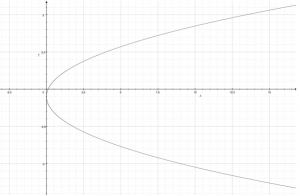
Risoluzione (2)
Prendiamo sull’arco di parabola situato nel 4° quadrante un punto S in modo che
$ \bar{SH} + \bar{SK} = \bar{CP}$

Sapendo che il punto S appartiene alla parabola, possiamo indicare le sue coordinate in questo modo:
$ S ( 4/9 y^2 + 4/9 y + 1/9 ; y) $
Calcoliamo la distanza fra il punto C(1;1) e il punto P(1;-2), considerando che essi appartengono alla stessa retta:
$ \bar{CP} = 1 – (-2) = 3 $
Allo stesso modo possiamo calcolare le distanze di S dagli assi, sottraendo la coordinata più piccola a quella più grande:
$ \bar{SH} = y_H – y_S = 0 – y = – y$
$ \bar{SK} = x_S – x_K = 4/9 y^2 + 4/9 y + 1/9 – 0 = 4/9 y^2 + 4/9 y + 1/9 $
Impostiamo ora l’equazione:
$ – y + 4/9 y^2 + 4/9 y + 1/9 = 3 $
$ – 9 y + 4 y^2 + 4 y + 1 = 27 $
$ 4 y^2 – 5 y – 26 = 0 $
$ y = frac(5 ± sqrt(25 + 4 * 4 * 26))(4 * 2) = frac(5 ± sqrt(25 + 416))(8) = $
$ frac(5 ± sqrt(441))(8) = frac(5 ± 21)(8) $
Dal momento che il punto P deve essere posto nel quarto quadrante, sappiamo che la sua ordinata è negativa; quindi escludiamo il risultato positivo.
$ y = frac(5 – 21)(8) = – frac(16)(8) = – 2$
$ x_S = 4/9 * (-2)^2 + 4/9 * (-2) + 1/9 = 4/9 * 4 – 4/9 * 2 + 1/9 = $
$ (16)/9 – 8/9 + 1/9 = frac(16 – 8 + 1)(9) = 9/9 = 1$
Di conseguenza, il punto S di coordinate (1;-2) coincide con il punto P.