Nel caso delle once acustiche, abbiamo parlato del fenomeno dell’interferenza, e abbiamo visto che ci sono dei casi in cui l’interferenza è costruttiva, e altri in cui è distruttiva.
Nel primo caso le onde che adiamo a sovrapporre sono tali per cui i rispettivi punti di massimo e di minimo corrispondono, nel secondo caso, invece, in presenza del minimo di un’onda vi è il massimo dell’altra.
In generale, sia che le onde diano un’interferenza costruttiva, sia che diano un’interferenza distruttiva, si dice che le sorgenti che le emettono sono coerenti quando la differenza di fase delle onde emesse rimane costante nel tempo.
Vediamo ora alcune condizioni che permettono di stabilire quando l’interferenza tra due onde, le cui sorgenti sono coerenti, sia un’interferenza costruttiva.
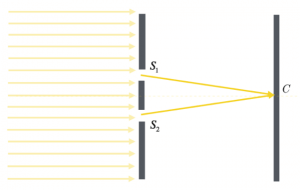
Consideriamo due onde $φ_1$ e $φ_2$ che si intersecano in uno stesso punto, situato a distanze diverse dalle rispettive sorgenti. Le onde in questione, però, giungono nel punto P sempre in fase, cioè ogni volta che il massimo di $φ_1$ si trova nel punto P, si intersecherà sempre con il massimo di $φ_2$, e ogni volta che vi sarà il minimo dell’una, vi sarà anche quello dell’altra.
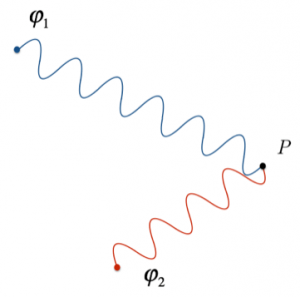
In questo caso, la differenza delle distanze dalle sorgenti al punto P è costante; si può affermare che se la differenza delle distanze delle sorgenti dal punto P è uguale ad un multiplo intero della lunghezza d’onda delle due onde identiche emesse da queste, allora la sovrapposizione delle onde nel punto P da luogo ad un’interferenza costruttiva.
$d(S_1 , P) – d(S_2 , P) = kλ $
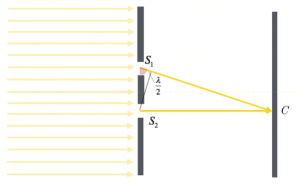
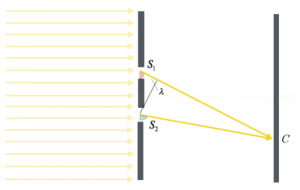
Come possiamo immaginare, nel caso in cui in un punto Q le onde si intersechino in modo che, in presenza del massimo di una si sovrappone il minimo dell’altra, si avrà interferenza distruttiva.
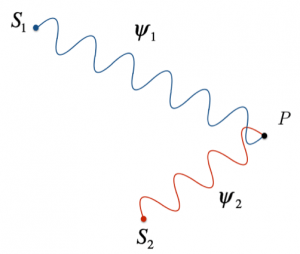
Possiamo, quindi, affermare che le sorgenti identiche che emettono onde identiche ψ1 e ψ2 danno interferenza distruttiva se la differenza delle loro distanze dal punto Q è uguale ad un multiplo intero della lunghezza d’onda sommato alla metà della lunghezza d’onda stessa:
$d(S_1 , Q) – d(S_2 , Q) = kλ + λ/2$
Notiamo che, in entrambi i casi, la sostante k può anche assumere valori negativi, nel caso in cui la distanza della prima sorgente dal punto considerato sia minore della seconda.
Esercizio
Consideriamo due sorgenti luminose che emettono onde uguali di lunghezza d’onda pari a $8,0 * 10^(-7)m$; supponiamo che le onde emesse si incontrino in un punto P distante, dalle rispettive sorgenti, rispettivamente $d_1=120 * 10^(-7)m$ e $d_2=364 * 10^(-7)m$. In base alle informazioni fornite, l’interferenza tra le due onde sarà costruttiva o distruttiva?
Per rispondere alla domanda, operiamo sulle rispettive distanze delle due sorgenti rispetto al punto di incontro. Calcolando la loro differenza, e relazionandola alla lunghezza d’onda delle onde emesse, possiamo capire che tipo di interferenza si creerà tra le due onde:
$d_1 – d_2 = 120 * 10^(-7) – 364 * 10^(-7) = -244 * 10^(-7) m $
Dato che questo valore non è un multiplo intero della lunghezza d’onda, possiamo concludere che l’interferenza non sarà costruttiva.
Vediamo ora se riusciamo a trovare un intero relativo k che soddisfa la seguente equazione:
$d_1 – d_2 = (k + 1/2)λ $
Ricaviamo k:
$k = frac(d_1 – d_2)(λ) – 1/2 $
Sostituiamo i valori numerici:
$k = frac(-244 * 10^(-7))(8,0 * 10^(-7)) – 1/2 = 30$
Concludiamo che interferenza tra le onde è di tipo distruttivo.
L’interferenza della luce
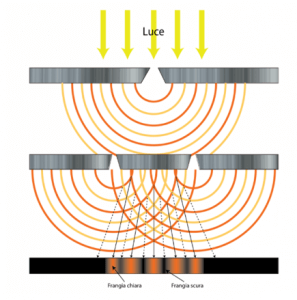
L’interferenza nel caso delle onde luminose si può osservare con un semplice esperimento.
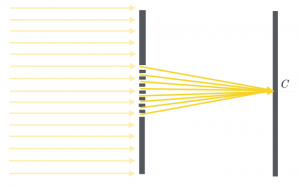
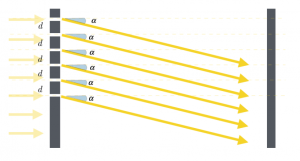
Si considera una parete liscia che presenta due fenditure parallele. L’esperimento consiste nel proiettare un fascio di luce monocromatica sulla parete, ed osservarne i fenomeni che si creano su una parete retrostante; si esaminano due casi: quando una delle due fenditure è chiusa e quando entrambe siano aperte.
Nel primo caso si proietta la luce sulla parete chiudendo una delle due fenditure; si osserva sulla parete retrostante una striscia di luce continua di forma rettangolare.
Se, invece, lasciamo aperte entrambe le fenditure, sulla parete retrostante osserviamo, nella superficie del rettangolo precedente, strisce di luce intervallate da strisce di ombra.
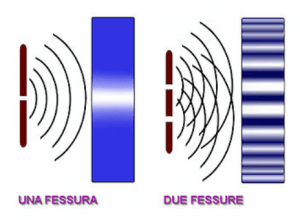
Possiamo interpretare questo fenomeno dicendo che nelle zone luminose si ha interferenza costruttiva tra le onde provenienti dalle due fenditure; nelle zone scure, invece, si ha interferenza distruttiva.
L’individuazione di questo comportamento da parte della luce ha permesso l’affermazione della teoria ondulatoria su quella corpuscolare; infatti il fenomeno dell’interferenza è un fenomeno tipico delle onde.
Potrebbero interessarti
Video lezioni: La luce
Appunti: L’esperimento di Young
Appunti: La diffrazione della luce
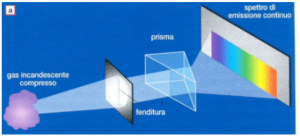
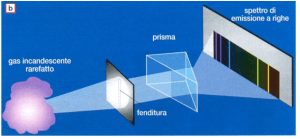
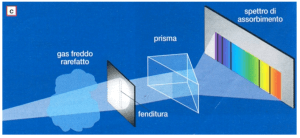
Appunti: Lo spettro della luce