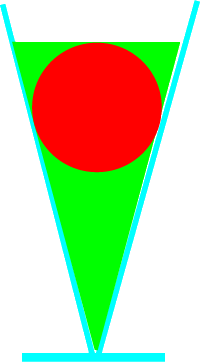
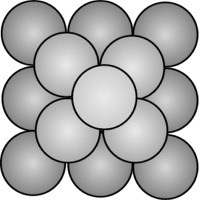
 |
La piramide dell'armiere In un deposito di munizioni sono ammucchiate alla rinfusa numerose palle di cannone il cui diametro misura 25 centimetri. Il capitano, amante dell’ordine e della geometria, ritiene che con esse si possano formare piramidi a base quadrata, accostando le sfere l’una all’altra e appoggiando quelle degli strati superiori negli interstizi creati da quelle sottostanti. Quante palle potranno essere, realmente, collocate in ogni piramide?
|
|
|
Autore: Antonio Bernardo
Gioconda
 |
La Gioconda L’orlo inferiore del celebre dipinto “La Gioconda” (77×53 cm) è posto a 15 cm al di sopra dell’occhio di un visitatore. Supponendo che la migliore visione del dipinto si abbia quando l’angolo sotteso dal quadro è massimo, a quale distanza dalla parete si deve mettere il visitatore ? |
Il problema non presenta particolari difficoltà se si sceglie di risolverlo per via trigonometrica.
Aurelio Mascheroni ha inviato la seguente soluzione con allegato il foglio Excel . Francesco Vinciprova l’ha risolto in questo modo . Questa è la soluzione di Marco Faini. La soluzione di Maurizio Morandi è un po’ diversa. Infine presentiamo la soluzione originale di Nora Morosi eseguita con Excel .
Molecola
 |
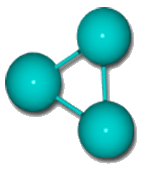Una molecola particolare Il Centro di Ricerche di Matematicamente sta studiando le proprietà fisiche di una nuova molecola di recente scoperta. Tale molecola è composta da 3 atomi di uno stesso elemento che si possono considerare puntiformi , non allineati e aventi distanza fissa fra loro; la molecola assume particolarità notevoli se viene drogata immettendo due elettroni che possiamo supporre ruotanti su un’orbita circolare, la prima inscritta nella molecola la seconda circoscritta ad essa. Il drogaggio viene effettuato tramite due laser conoscendo la distanza fra i centri delle due orbite. Qual è tale distanza ? (Dalle tabelle della fisica atomica e con un po’ di calcoli sono note le misure delle altezze relative ai tre lati formati dalla molecola: 49,2 nm, 65,6 nm, 57 nm.) |
| soluzione | |
Il problema proposto poteva essere risolto abbastanza facilmente se si usava la relazione di Eulero fra centri e raggi delle circonferenze inscritta e circoscritta ad un triangolo. Un gruppo di risolutori ha seguito questa strada e fra tutti segnaliamo la soluzione di Danilo Mascheroni .
Un altro gruppo di risolutori ha invece sfruttato la geometria analitica, per esempio Marcello Falco .
Albergo
 |
Albergo da ampliare I gestori di un albergo prevedono di ampliare l’albergo stesso fino a raggiungere un numero di 200 stanze. Ogni stanza sarà dotata di un apparecchio telefonico. Al fine di spendere il meno possibile è stato deciso di utilizzare un centralino che serva i 200 apparecchi telefonici e abbia n linee in uscita. L’obiettivo dei gestori è di installare il minor numero possibile di linee in uscita, garantendo però ai propri clienti di trovare una linea libera almeno al 99% dei tentativi di chiamata. |
| soluzione |
soluzione Servono almeno 7 linee
Il simulatore del sistema di Pablo (Paolo Furlani)
I risultati delle simulazioni con 6 linee [125 kB] e 7 linee [131 kB] .
La soluzione di Luca Barletta:
Cerchiamo di inquadrare correttamente il problema: c'è una popolazione finita (i clienti dell'albergo) che si contende un mezzo condiviso (le linee in uscita); lo scopo è quello di mascherare al 99% la presenza del mezzo condiviso agli utenti.
Ogni utente genera un tasso di chiamate al giorno (3 ch/giorno -> 2,083*10^(-3) ch/min) e il centralino è in grado di smaltire un altro tasso di chiamate al minuto (5 min/ch -> 0,2 ch/min). Possiamo asserire che in media ogni utente offre un traffico:
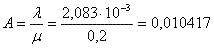
Questo sistema lo possiamo riassumere in una rappresentazione a stati: ogni stato del sistema è caratterizzato dal numero di utenti che stanno usufruendo del servizio; si può solo passare da uno stato i al successivo i +1, evento in cui un utente inizia una chiamata (per ipotesi non arrivano più chiamate contemporaneamente), e si può passare dallo stato i al precedente i -1, evento in cui un utente termina una chiamata.
Logicamente avremo N +1 stati (da 0 a N , con N incognita del problema).
Bisonga determinare con quale tasso si passa da uno stato al successivo e da uno stato al precedente:
- Quando passiamo da uno stato al successivo, significa che un utente ha appena iniziato una chiamata; indicando con S la popolazione totale e con i lo stato corrente, la probabilità di passare dallo stato i a quello i +1 è:
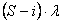
- Quando passiamo da uno stato al precedente, significa che un utente ha appena terminato una chiamata; indicando con i lo stato corrente, la probabilità che il centralino liberi una linea è:
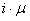
Ecco uno schema esplicativo del diagramma a stati del sistema:
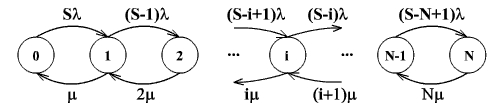
Dobbiamo trovare la probabilità di trovarci in un dato stato del sistema, ovvero la probabilità che ci siano i utenti in linea.
Cominciamo col scrivere l'equazione d'equilibrio per gli stati 0 ed 1; indicando con pi_greco(i ) la probabilità di trovarsi nello stato i -esimo si ricava la seguente:
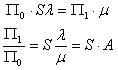
scriviamo la stessa equazione per gli stati 1 e 2:
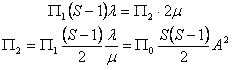
iteriamo il procedimento fino allo stato i -esimo:
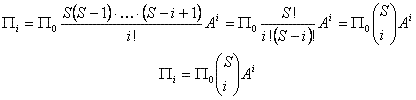
La somma di tutte le probabilità deve essere unitaria:
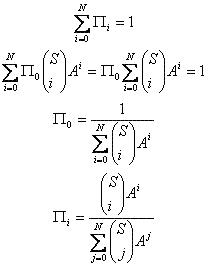
Ora è possibile calcolare la probabilità di perdita.
Non bisogna commettere l'errore di confondere la probabilità di perdita di una chiamata con la probabilità di blocco del sistema. Infatti il sistema si dice in blocco una volta raggiunto lo stato i -esimo, mentre si ha la perdita di una chiamata quando, raggiunto lo stato di blocco del sistema, un nuovo utente tenta di chiamare.
Pertanto si può impostare la seguente relazione:
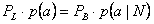
dove al primo membro troviamo il prodotto tra la probabilità di perdita e la probabilità istantanea che un utente chiami, al secondo membro troviamo il prodotto tra la probabilità di blocco e la probabilità istantanea che un utente chiami sapendo che ci sono già N utenti in linea (lo stato è in blocco).
Le probabilità istantanee di chiamata sono:
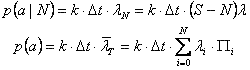
A noi interessa la probabilità di perdita:
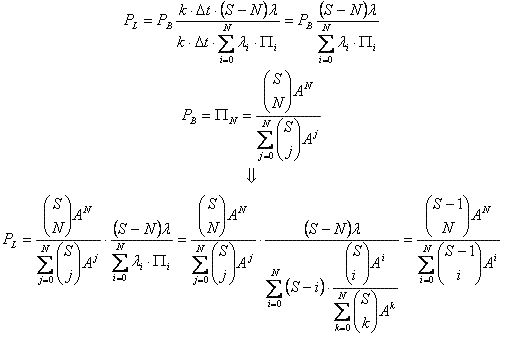
Pertanto dovremo risolvere la seguente disequazione in N , con N numero intero positivo:
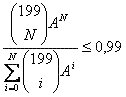
Per la risoluzione utilizzo un foglio di calcolo [101 kB] Excel, trovando N =7.
Cavo elettrico
 |
Un cavo elettrico
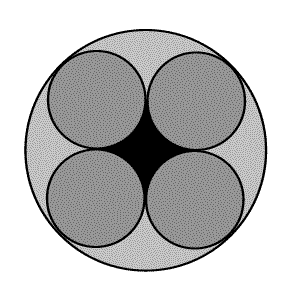
Un cavo elettrico di raggio 1 cm contiene al suo interno altri quattro cavi elettrici di uguali dimensione, come in figura. Quanto misura l'area di colore nero, della sezione del cavo? Si suppongano le superfici di spessore trascurabile. |
A = (4 – pi_greco) * (3 – 2*sqrt(2)) = 0,147…
La motivazione di Cate (Roma):
Definiti:
d = distanza tra i due centri (centro circonferenza grande e centro circonferenza piccola)
r = raggio circonferenza piccola
R = raggio circonferenza grande
d = R-r
R = 1
d = r*(sqrt)2
r = (sqrt)2 -1
Area_C(cerchio grande) = pi_greco
Area_c(cerchio piccolo) = pi_greco*(3-2*(sqrt)2)
Area_t(triangolo rettangolo con ipotenusa d e cateti r) = (r*r)/2 = (3-2*(sqrt)2)/2
Area_spicchio_c = Area_c/8 = (pi_greco*r*r)/8
Area_nero = 8(Area_t – Area_spicchio_c) = ..sostituendo e approssimando.. = 0.85841*0.1716 = 0.1473
Un nuovo sistema di numerazione
E’ stato inventato un nuovo sistema di rappresentazione dei numeri. Si utilizzano due simboli: # e @. Il simbolo # in fondo ad una sequenza significa aggiungere un’unità, mentre il simbolo @ significa moltiplicare per 7. Ad esempio la sequenza #@##@# rappresenta il numero 64. Qual è il minor numero di simboli per rappresentare il numero 1000?
La soluzione più completa pervenutami è quella di Frigate :
Regole per la costruzione di rappresentazioni minime (col minor numero di simboli):
1) Una rappresentazione minima inizia sempre con il simbolo #.
esempio:
# # #
@ # # #
@ @ # # #
@ … @ # # #
sono rappresentazioni dello stesso numero.
La prima contiene il numero minimo di simboli.
2) Data una rappresentazione minima, quella del numero successivo si ottiene aggiungendo il simbolo #.
esempio:
# # @
la successiva e’
# # @ #
3) Se applicando la regola 2) si ottiene una rappresentazione in cui compare la sequenza ‘ @ # # # # # # # ‘, questa viene sostituita con la coppia ‘ # @ ‘.
Infatti, ‘ @ # # # # # # # ‘ corrisponde all’ espressione ‘ y*7+7 ‘ che puo’ essere sostituita da ‘ (y+1) * 7 ‘.
esempio:
# @ # # @ # # # # # # # e # @ # # # @
rappresentano lo stesso numero, ma la seconda e’ in forma minima.
esempio:
# # @ # # # # # # @ # # # # # # #
diventa
# # @ # # # # # # # @
poi
# # @ # # # # # # # @
diventa
# # # @ @
4) Un numero della forma x = 7^n, verra’ rappresentato nel seguente modo:
# @ @ …. @ dove i simboli @ sono n.
esempio:
il numero 7 si puo’ rappresentare come
# # # # # # #
si puo’ vedere come
@ # # # # # # #
quindi per la regola 3) si ha
# @
esempio:
il numero 7^3 = 343 si puo’ rappresentare come
# # # # # # @ # # # # # # @ # # # # # # #
diventa
# # # # # # @ # # # # # # # @
diventa
# # # # # # # @ @
si puo’ vedere come
@ # # # # # # # @ @
diventa
# @ @ @
5) Dalle precedenti regole segue che una rappresentazione minima puo contenere una sequenza di simboli # consecutivi, al piu’ di lunghezza 6.
Volendo trovare la rappresentazione minima di un numero X, evidenziamo il quoziente e il resto della divisione di X per 7:
X = Q * 7 + R
Tenendo conto della regola 5) e di quanto detto in precedenza, la rappresentazione minima di X si ottiene applicando ricorsivamente la seguente formula:
M( X ) = M( Q ) | @ | #( R )
dove
#( R ) indica un numero di simboli # pari a R.
M( X ) indica la rappresentazione minima di X.
M( Q ) indica la rappresentazione minima di Q.
Adesso, sfruttando la formula prcedente, calcoliamo la rappresentazione minima di X = 1000.
X = 1000 —> Q = 142, R = 6
da cui
M( 1000 ) = M( 142 ) | @ | #( 6 )
X = 142 —> Q = 20, R = 2
da cui
M( 142 ) = M( 20 ) | @ | #( 2 )
X = 20 —> Q = 2, R = 6
da cui
M( 20 ) = M( 2 ) | @ | #( 6 )
X = 2 —> Q = 0, R = 2
da cui
M( 2 ) = M( 0 ) | @ | #( 2 ) = #( 2 )
Componendo i risultati si ha:
M( 1000 ) = #( 2 ) | @ | #( 6 ) | @ | #( 2 ) | @ | #( 6 )
ovvero
M( 1000 ) = # # @ # # # # # # @ # # @ # # # # # #
La soluzione di RobertoC75 :
##@######@##@######
I simboli @ trovati a sinistra del primo # non hanno influenza sul numero poiche’ andrebbero a moltiplicare 0 * 7.
(((1+1)*7 +1+1+1+1+1+1)*7 +1+1)*7 +1+1+1+1+1+1 = 1000
Per trovare la soluzione ho scritto un piccolo algoritmo, lasciando al calcolatore l’onere di controllare tutte le possibili combinazioni (in fondo il sistema @# e’ un sistema binario). Altre soluzioni richiedono ovviamente piu’ simboli.
La soluzione diBooDoo :
Il numero è ##@######@##@######
Per ottenerlo sono partito dalla fine effettuando le due operazioni di divisione tra interi e di modulo tra 1000 e 7 ottenendo 142 e 6.
A questo punto ho iniziato a scrivere il numero dalla fine inserendo 6 simboli # e 1 simbolo @ (@######); ho quindi reiterato le stesse operazioni tra 142 e 7 ottenendo 20 e 2.
Ho quindi aggiunto, da destra verso sinistra 2 # e 1 @ (@##@######); ho quindi reiterato le stesse operazioni tra 20 e 7 ottenendo 2 e 6 e il numero è diventato @######@##@######.
Per finire tra 2 e 7 ho ottenuto 0 e 2 ed il numero finale è ##@######@##@######.
Continuando a rifletterci ho trovato un secondo metodo risolutivo molto più elegante;
Scrivendo il numero 1000 in base 7 si ottiene 2626 che si può riscrivere utilizzando il nostro sistema di numerazione proprio come ##@######@##@###### dove indico le cifre con un uguale numero di simboli # e il simbolo @ è un separatore.
Faccio un altro esempio 49 in base 7 diventa 100 e nel nostro sistema #@@ dove il valore 0 sorrisponde a 0 simboli #.
Un cubo da costruire
Luca vuole realizzare un cubo di carta. Disegna su un foglio le sei facce, ritaglia il contorno, lo piega e lo incolla con il nastro adesivo. In quanti modi differenti può disegnare il cubo? Il disegno deve essere costituito da un pezzo unico, come quello riportato in figura. Due disegni sono equivalenti se un movimento o un ribaltamento del foglio porta a coincidere i due disegni.
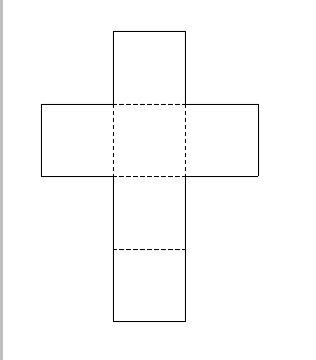
11 disegni in totale
di cui 6 con 4 facce centrali
4 con 3 facce centrali
1 con 2 facce centrali
Giallo a Camelot
|
Giallo a Camelot
Nel regno di Camelot è appena capitata una disgrazia: qualcuno ha rubato Excalibur, la mitica spada di re Artù; senza di essa il regno potrebbe cadere sotto il dominio dei nemici. – Galeotto ha un figlio che è stato escluso dalla stretta élite dei cavalieri, per espresso volere di Artù;
– Lancillotto scagiona Galeotto perché gli è stato riferito che la sera del fatto era in una locanda assieme ad altri cavalieri; inoltre afferma che Otto è molto legato al fratello. Merlino, con un pizzico di magia, riesce a capire che uno solo di loro mente, ma non necessariamente il colpevole.
|
Per risolvere il quesito occorre capire quale dei tre sta mentendo, e desumere quindi l'identità del ladro.
Partendo dal presupposto che una persona è innocente finché non ne viene provata la colpevolezza, possiamo definire le seguenti proposizioni, che assumono il valore logico "vero":
- R = Galeotto dice il vero
- P = Otto dice il vero
- Q = Lancillotto dice il vero
- B = Lancillotto è innocente
- C = Galeotto è innocente
- A = Otto è innocente
Trasformo poi in forma proposizionale le affermazioni contenute nell'interrogatorio di Merlino, assumendo che se un testimone dice la verità allora la sua affermazione è vera.
- P -> B poiché Otto è sicuro che Lancillotto non uscì dalle sue stanze
- P -> R poiché per Otto Galeotto è onesto (onesto <=> dice la verità)
- Q -> C poiché Lancillotto dice che Galeotto era alla locanda
- R -> A poiché Galeotto dice che Otto era ad una festa di corte
- Q -> P poiché per Lancillotto Otto è onesto
Se tutti i testimoni avessero detto la verità, tutte le implicazioni sopra riportate sarebbero vere e quindi varrebbe la relazione:
M = (P -> B) e (P -> R) e (Q -> C) e (R -> A) e (Q -> P) = "vero"che porterebbe a concludere che non c'è un ladro.
Di conseguenza almeno una delle affermazioni deve essere falsa. Per trovare quella falsa costruiamo una tabella di verità.
N.B. Per evitare di costruire tutti i possibili 64 casi, consideriamo solo quelli che prevedono un solo colpevole e un solo bugiardo, cioè quelli in cui una sola delle proposizioni A, B e C è falsa e una sola tra P, Q e R è anch'essa falsa.
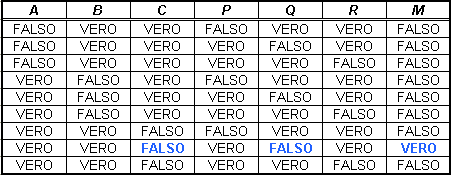
La sola riga che porta alla conclusione di implicazioni nel complesso vere, e quindi che corrispondono alla realtà dei fatti veramente accaduti, è l'ottava. Di conseguenza si può riconoscere che le proposizioni false in partenza sono C e Q, cioè:
- è falso che Galeotto è innocente, dunque è colpevole
- è falso che Lancillotto dice il vero, quindi è bugiardo
Luca Barletta
Secondo e terzo arrivato
 |
Secondo e terzo arrivato
Nel campionato di Formula 1 sono andati a punti 18 piloti. In totale i punti realizzati sono stati 442. Sapendo che Schumacher, primo arrivato, ha raggiunto 144 punti, quanti punti devono aver raggiunto, singolarmente, come minimo il secondo e il terzo arrivato? |
Nel quesito si fa riferimento alla Formula 1 che ha un complesso metodo di assegnazione dei punteggi. Poiché non erano state esplicitate quali erano le regole di assegnazione dei punteggi e di conclamazione dei vincitori, sono state accettate diverse soluzioni.
Nell'ipotesi in cui più concorrenti possono arrivare con lo stesso punteggio e che il secondo e il terzo arrivato vengano stabiliti in base ad altri criteri, tipo migliori piazzamenti nelle prove, la soluzione si ottiene da
442-144=298 i punti rimanenti. Divisi tra i 17 piloti rimanenti si ottiene 17,5 punti a testa, che possono essere distribuiti assegnando 18 punti a 16 piloti e 10 punti all'ultimo pilota. I punti rimanenti possono essere distribuiti anche in altro modo. La soluzione è quindi 18 per il primo e 18 per il secondo.
Se il secondo e il terzo devono avere uno scarto di un punto la soluzione è 20 per il secondo, 19 per il terzo, 18 per il quarto, ecc.
Se si cerca il punteggio minimo in totale del secondo e terzo, il modello matematico corretto è quello descritto da Danilo Mascheroni che però contiene anche l'ipotesi aggiuntiva che gli ultimi piloti abbiamo raggiunto tutti lo stesso punteggio.
p2 + p3 +15*p4 = 298 (1)
poiché p2 > p3 > p4 si può porre:
p2 = p4 + D2
p3 = p4 + D3
dove D2 e D3 sono per definizione le differenze fra i punteggi con D2 > D3.
La (1) diventa allora:
17*p4 + D2 + D3 = 298
p4 = (298 – (D2 + D3))/17
Il più piccolo valore di D1+ D2 per il quale p4 risulta intero è D1 + D2 = 9, con p4 = 17.
Si hanno allora le seguenti combinazioni dei due punteggi:
(25,18)
(24,19)
(23,20)
(22,21)
Quindi il secondo arrivato ha raggiunto almeno i 22 punti, il terzo ha raggiunto almeno i 18.
La soluzione di Brioschi Marco Attilio tiene conto del regolamento ufficiale della Formula 1, che si può trovare per esempio ai seguenti indirizzi:
http://digilander.libero.it/cronoF1/regolamento.html – http://ferrari.netcat.it/regolamento.html
Una possibile situazione è la seguente: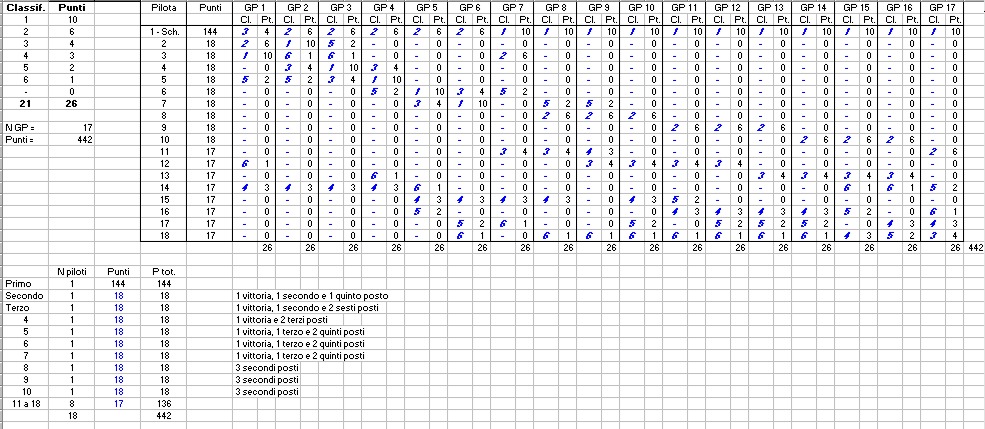
La soluzione di Cesare Proto tiene conto dei punti realizzati da Schumacher nel campionato di Formula 1 e ha ottenuto la seguente classifica possibile
Un cubo segato
 |
Un cubo segato Un cubo di legno di 8 cm di lato è stato dipinto di bianco. Successivamente è stato tagliato in cubetti da 1 cm di lato. I cubetti ottenuti hanno alcune facce dipinte di bianco, altre non dipinte. Volendo dipingere tutti i cubetti di bianco, qual è la superficie delle facce da dipingere? |
La superficie dipinta del cubo è 384 cm2
8*8*8 = 512 i cubetti di cui si compone il cubo grande
La superficie di tutti i cubi piccoli è 6*512 = 3072 cm2
La superficie da dipingere è 3072cm2 – 384cm2 = 2688cm2
Puzzle
 |
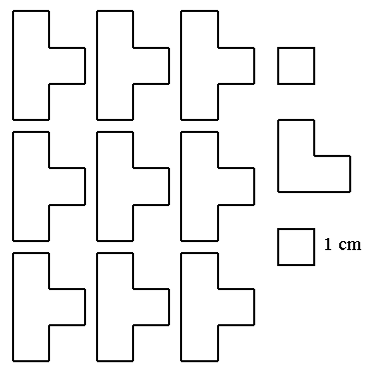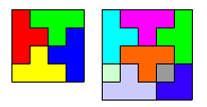
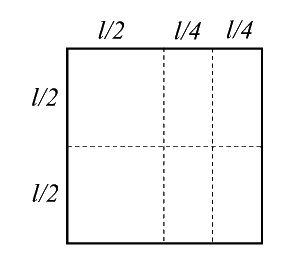
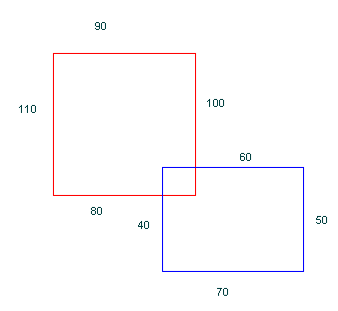
Il puzzle Antonio e Marcello ritagliano due cartoncini quadrati di misure differenti per formare un puzzle. Decidono di tagliare i due quadrati in pezzi di forme uguali. Marcello ci è riuscito, Antonio no. Alla fine i pezzi ottenuti sono quelli della figura a fianco. Quali erano le dimensioni dei quadrati originari? |
Il totale dei quadrati da 1 cm è 41. Occorre trovare due quadrati la cui somma sia 41, quindi 25+16.
Esercizio sbagliato
 |
Un esercizio sbagliato Mario si esercita sui numeri relativi. Deve trovare il risultato della somma dei numeri da 1 a cento, i numeri dispari sono positivi, quelli pari sono negativi. +1-2+3-4+5-6+7-8+9-10+11 … -96+97-98+99-100. Il risultato trovato è +50. In realtà ha commesso un errore, un solo errore di segno. Qual è il numero inserito con il segno errato nella calcolatrice?
|
Il risultato doveva essere S= (1-2) + (3-4) + (5-6) … +… +(99-100) = (-1) + (-1) + (-1)… +… +(-1) = -50. Mario ha invece ottenuto +50. L'errore è stato di 100, pertanto l'unico numero che raddoppiato dà 100 è 50.
A prima vista il numero errato sembrerebbe 100 … invece è 50.
Il calcolo di JORDAN:
S = ( 1 + 3 +5 +… + 99 ) – ( 2 + 4 + 6 +…+ 100 ) = D – P = -50
Inserire il numero N con il segno sbagliato equivale ad esempio a sottrarlo da P (D) ed aggiungerlo in D (P) e la somma errata S' diviene:
S' = ( D + N ) – ( P – N ) = ( D – P ) + 2N = S + 2N = 50
Pertanto:
2N = 100 e quindi N = 50.
Tessere
Fiore
 |
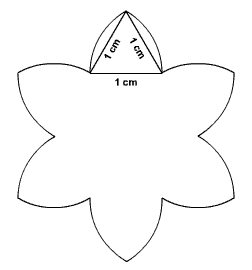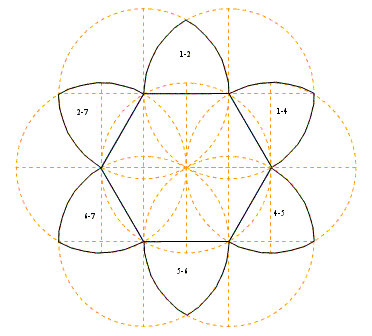
Fiore Loris ha visto una figura del suo libro di geometria e la vuole riprodurre, ma ha a disposizione solo un foglio bianco senza quadrettatura e un compasso con apertura fissa a 1 cm (l’apertura non si può modificare). Quante volte, come minimo, Loris dovrà avvalersi del compasso? |
Minimo 7 volte
L'animazione di Mauro Procaccini :
La costruzione di Roberto Corradin :
Dividere un quadrato
 |
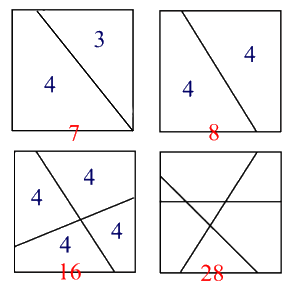Dividere un quadrato Un segmento che congiunge due lati di un quadrato divide il quadrato in due poligoni. Nel primo caso disegnato i poligoni hanno rispettivamente tre lati e quattro lati. La somma dei lati dei due poligoni ottenuti è 7. Nel secondo caso, lo stesso quadrato è stato diviso da un segmento congiungente due lati in due poligoni di quattro lati. La somma dei lati dei poligoni in questo caso è maggiore, 8. Utilizzando 7 segmenti congiungenti due lati del quadrato, qual è il numero massimo di lati di poligoni ottenibile? |
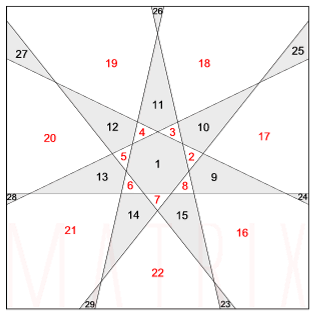
La soluzione di Matrix Teramo
| Sono stati prolungati i 7 lati dell'ettagono regolare (1), fino al quadrato di contorno. In questo modo si ottengono 7 segmenti che generano il massimo numero di nodi interni (e quindi il massimo numero di poligoni). Ogni segmento, infatti, interseca gli altri sei, oltre naturalmente a due lati del quadrato.
Si ottengono quindi 29 poligoni: Il numero complessivo dei lati è pertanto 116. |
 |
L'idea di Giancod Roma
Ho trovato la seguente regola: se con K segmenti si ottengono al massimo N lati, con K+1 segmenti se ne ottengono al massimo N+4(K+1).
Per cui
K=1 –> N = 8.
K=2 –> N = 8 + 4x(2) = 16
K=3 –> N = 16 + 4x(3) = 28
…………………………………….
K=6 –> N = 64 + 4x(6) = 88
K=7 –> N = 88 + 4x(7) = 116
La generalizzazione di Leon Teramo
Generalizziamo il problema: qual è il numero massimo di lati dei poligoni ottenibili utilizzando n corde congiungenti due lati del quadrato (con n>=2). Il massimo si ottiene quando:
1) ogni corda interseca due lati del quadrato in due punti diversi dai vertici
2) ogni corda è intersecata in n-1 punti dalle rimanenti n-1 corde
Nella figura che si ottiene rispettando le condizioni 1), 2) i lati dei poligoni, giacenti sul contorno del quadrato originario, sono 2n+4 e vanno contati una sola volta; i lati dei poligoni , interni al quadrato sono n*n ma ognuno di essi dev'essere contato due volte. Pertanto il massimo numero dei lati di tutti i poligoni che si vengono a formare è
f(n) = 2n^2 +2n + 4 , per ogni n>=2 [ f(1)=8 ]
Per n=7 si ottiene f(7) = 116.
Una bella costruzione di Ucando Gallarate (VA)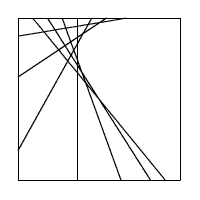
La suddivisione "artigianale" di Amelia Milano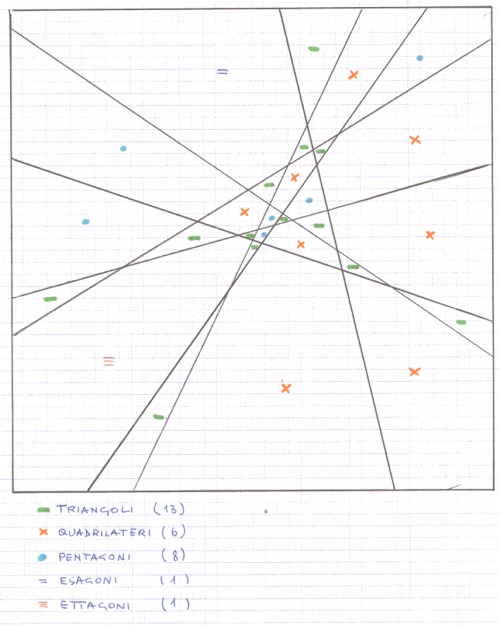
Un furto
|
Un furto In un albergo c'è stato un furto. L'ispettore interroga uno per volta le nove persone che alloggiano sul piano dove è avvenuto il furto. Ivano : Sono uscito dalla mia stanza alle 20:00 e sono rientrato alle 20:15. Ho dimenticato di chiudere a chiave la porta e al mio ritorno non ho più trovato i soldi che avevo nascosto nella cassaforte. Per aprire e richiudere la cassaforte occorrono almeno 6 minuti. Antonio : Sono andato a trovare Bruno verso le 19:30, sono stato nella sua stanza fino alle 20:05. Poi sono rientrato nella mia stanza per vedere la partita in televisione. Alle 20:10 ho telefonato a Bruno per chiedergli se voleva vedere la partita con me, ma non mi ha risposto nessuno. Dopo è venuto Gianni e abbiamo visto insieme la partita. Bruno: E' venuto a trovarmi Antonio e siamo stati a lungo insieme. Poco dopo, sono andato a trovare Carlo per qualche minuto e poi sono andato da Domenico a vedere la partita. Mentre andavo da Domenico ho incontrato Gianni nel corridoio. Gli orari non me li ricordo. Carlo : Alle 20:00 c'era già Marcello da me, se n'è andato quando è venuto Francesco. Quando se n'è andato Francesco ho telefonato a Marcello, ma la linea era occupata. Poi Marcello è venuto a trovarmi con Bruno: sono stati appena tre minuti. Un minuto dopo sono andato da Domenico a vedere la partita. Uscendo dalla mia stanza ho incontrato Bruno che stava andando anche lui da Domenico e siamo andati insieme. Domenico : Sono stato da Emilio fino alle 20:05 poi me ne sono andato nella mia stanza. Dopo un po' ho telefonato a Francesco. Nella sua stanza c'era Emilio, li ho invitati a vedere la partita ma non sono voluti venire. Sono venuti invece Bruno e Carlo. Emilio : Domenico è stato da me per un po'. Poi sono andato da Francesco e sono stato con lui a vedere la partita. Francesco : Sono rientrato in camera esattamente alle 20:00. Mentre rientravo ho visto Ivano che stava uscendo dalla sua stanza. Un minuto dopo è venuto Gianni. E' stato appena due minuti. Quando se ne è andato sono uscito per andare a trovare Carlo. Sono stato lì poco più di due minuti e sono rientrato nella mia stanza. Quando sono arrivato il telefono stava squillando: era Marcello. Abbiamo parlato per un paio di minuti. Tre minuti dopo è venuto Emilio. Gianni: Alle 20:00 sono uscito dalla mia camera per andare a trovare Francesco. Uscendo ho incontrato Ivano e ci siamo salutati. Abbiamo parlato per un minuto circa e poi sono entrato nella stanza di Francesco. Sono stato un po' lì. Rientrando ho visto Marcello nel corridoio. Ho visto la partita da Antonio. Mi ricordo che mentre andavo da Antonio ho visto Bruno e Marcello insieme nel corridoio. Marcello : Alle 20:00 mi trovavo sicuramente da Carlo. Poi sono tornato in camera. Dopo un po' ho chiamato Francesco al telefono. Abbiamo parlato un paio di minuti. Appena ho chiuso il telefono sono andato di nuovo da Carlo. Poi sono uscito dall'albergo. Mi ricordo di aver incontrato Gianni nel corridoio ma non mi ricordo quando. L'ispettore verifica tutte le dichiarazioni: sono tutte vere. Tuttavia, qualcuno di loro può aver commesso il furto. Chi? |
|
Il diagramma temporale ricostruito da Matrix Teramo, secondo cui solo Gianni può aver commesso il furto.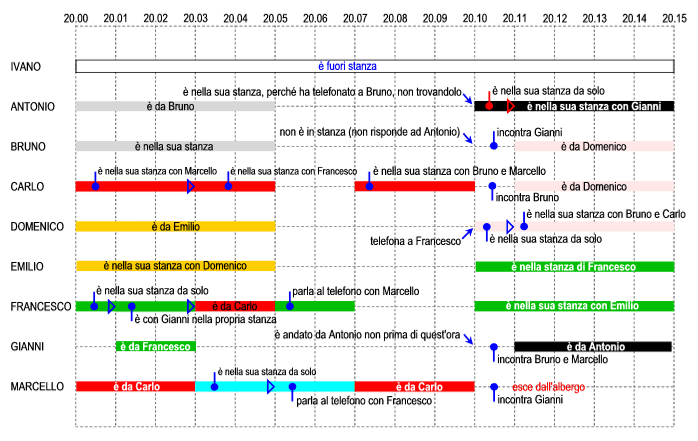
Quello di Leon Teramo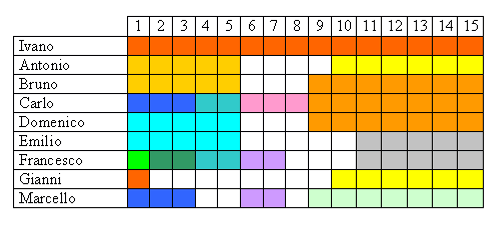
Lo sfogo di Lucrezia'shausband Palo del Colle (Ba)
Per compiere il furto ci vogliono 6minuti almeno. Esso è stato compiuto fra le 20.00 e le 20.15. Pertanto non dopo le 20.09.
Antonio è con Bruno fino alle 20.05 e telefona allo stesso alle 20.10.Antonio è innocente.
Bruno è con Antonio fino alle 20.05 che dalle 20.08 è in giro con gli amici e non si ritira più. Bruno, innocente.
Carlo è con qualcuno fino alle 20.05 e ha ospiti dalle 20.08 fino alle 20.11 e poi va da Domenico. Carlo assolto.
Domenico va via da Emilio alle 20.05 e telefona a francesco alle 20.11.Siccome ci vogliono almeno 6 minuti per il furto, Domenico salvo in extremis.
Emilio ha un ospite fino alle 20.05 e alle 20.11 è da Francesco. Non è lui il colpevole.
Marcello è da Carlo fino alle 20.03, telefona a Francesco alle 20.06 e dopo le 20.09 è da Carlo. Lui non sarà incriminato.
Gianni(Agnelli, Bettega, Moggi, Giraudo e tutta la razza loro)è stato da Francesco fino alle 20.03 poi rientra e vede Marcello sta in camera probabilmente per 2 minuti e lo rivedono solo alle 20.12 Bruno e Marcello.
Gianni in galera. Come volevasi dimostrare. La deve pagare! 26 scudetti rubati altro che soldi.
Cartoline
 |
Cartoline Marco riceve molte cartoline dai suoi amici. Ora vuole incollarle sull'armadio. Dire che è preciso è poco: è un vero maniaco della precisione. In primo luogo, vuole incollare il massimo numero di cartoline; in secondo luogo, vuole utilizzare il minimo di nastro adesivo. Ha già preso tute le misure. L'armadio è alto 180 cm, ha due ante, ciascuna di 45 cm. Le cartoline hanno tutte dimensioni 16cmX11cm. Alcune hanno l'immagine in un verso, altre nell'altro verso. Ne ha un centinaio per tipo. Il rotolo di nastro adesivo è largo 1,5 cm Le cartoline vanno incollate almeno lungo due lati opposti. Il nastro deve aderire almeno per 5 mm sulla cartolina e 5 mm sull'armadio. Le due ante devono continuare ad aprirsi separatamente
Quante cartoline può incollare? Di quanti cm di nastro adesivo ha bisogno? |
La soluzione migliore pervenuta è stata quella di Wonderp Rovereto (TN)
Marco attacca solo cartoline verticali, 44 per anta.
Nei 45 cm ce ne stanno 4 (11*4=44cm), nei 180 cm ce ne stanno 11 (16*11=176cm) il problema sta tutto nell'attaccarle.
Come si vede dal disegno (mi scuso per la rozzezza ma ho a disposizione solo Paint) la cartolina in alto a sx ha nastro sulle verticali, alla sua dx in nastro sporge sull'armadio per 5mm a sx è indifferente. La seconda cartolina in alto ha in nastro sopra e sotto ed andrà attaccata con il suo lato sinistro che combacia con in lato destro della prima (quindi la seconda copre solo il nastro della prima) e così via per la terza e la quarta, il disagno è da considerare un esploso e il nastro è rappresentato un po' interno solo per comodità). Il nastro sporge a sinistra della quarta cartolina per 5mm, quindi in orizzontale ho usato tutta l'anta: 0,5+11*4+0,5=45cm
La riga sotto va alternata rispetto alla prima, il consumo di nastro è uguale per le due righe. In verticale avevo 4 cm di avanzo (180-176=4cm) più che sufficenti per attaccare il nastro.
La quantità di nastro usato per una riga è 16*4+11*4=108cm, per le 11 righe 108*11=1188, per tutto l'armadio 1188*2=2376cm.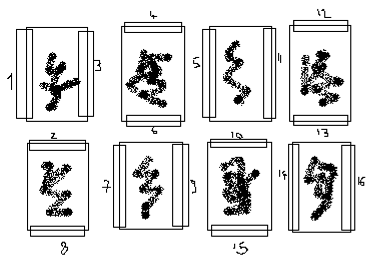
P.S. Ciò non è solo teorico si può fare realmente: si deve fissare il secondo lato di ogni cartolina solo dopo aver attaccato il primo lato della cartolina il cui nastro si infilerà sotto. I numeri nel disegno sono un ipotetico ordine.
L'interpretazione del testo non è facile ma la soluzione mi sembra corretta.
Interessante anche la soluzione di Shuty Genova
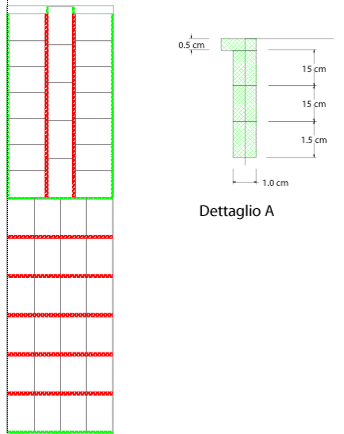
| Su ogni anta si incollano 43 cartoline secondo lo schema in figura.
I tratti da 0.5cm che separano 2 file di cartoline vengono coperti dal nastro di larghezza 1.5cm tagliato nella direzione "naturale", indicato dal colore rosso. I tratti esterni invece vengono coperti, per risparmiare, da pezzi di nastro lunghi 1.0cm posizionati ruotati di 90 gradi (come nel dettaglio A del disegno), indicati dal colore verde. I tratti con pezzi di nastro lunghi 1.0cm sommano 248 cm. Essendo questo numero non divisibile interamente per 1.5, occorre tagliare 165 cm di nastro a pezzi lunghi 1.0 cm più un pezzettino lungo 0.5 cm, posizionato come nel dettaglio A. Per ogni anta si utilizzano 374 cm di nastro disposto come quello rosso e 165,5 cm di nastro disposto come quello verde. In totale 539,5 cm |
 |
La scatola
Da un foglio di cartone quadrato di 100 cm di lato, ricavare la scatola di volume massimo. La scatola deve essere ottenuta ritagliando dal foglio di cartone le sei facce e incollandole con il nastro adesivo.
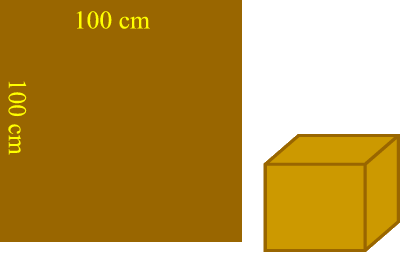
Un esempio di questo tipo viene spesso utilizzato nei libri di analisi per applicare la teoria dei massimi e minimi vincolati per le funzioni di due variabili. In realtà, almeno in questo caso i vincoli sono difficili da determinare. Si richiedeva un’ulteriore analisi del problema.
Dallo studio della funzione V=xyz con 2xy+2xz+2yz =A si ottiene la soluzione x=y=z=SQR(A/6), dove A è la superficie del cartone. La scatola di volume massimo sembrerebbe un cubo di lato 40,82 cm e volume 68041,38cm^3. A questo punto si pone il problema di verificare se è possibile ritagliare i sei quadrati di lato 40,82. Infatti la condizione 2xy+2xz+2yz=A riguarda soltanto la superficie del cartone di partenza e non la sua forma.
La difficoltà del quesito doveva essere questa. Sono stato però superficiale nella scelta delle misure del cartone di partenza. Chi ha fatto tutti conti è caduto nella trappola che gli avevo ‘amichevolmente(?)’ teso, chi ha avuto un approccio più intuitivo è stato fortunato nell’imbattersi nella soluzione.
La soluzione ottimale si ottiene cercando di utilizzare tutta la superficie disponibile e allo stesso tempo di ottenere quante più facce quadrate possibili. Una dimostrazione rigorosa non ce l’ho e nessuno l’ha inviata.
Tra le soluzioni più complete quella di Vinciprova Francesco (.pdf) .
Una giornata di pioggia
|
|
Una giornata di pioggia
1. In una giornata di pioggia un ragazzo fa ruotare un ombrello aperto con l'asta verticale. Dal bordo dell'ombrello ad una altezza h=2m dal suolo e a distanza r=0.7m dall'asta si staccano delle gocce d'acqua che cadendo tracciano sul suolo una circonferenza di raggio R=1.5m. Trascurando ogni attrito, calcolare il tempo in cui l'ombrello compie un giro. |
L'ombrello compie un giro in circa 2,12 secondi
La motivazione di Danilo Mascheroni
La traiettoria della goccia (parabola) appartiene ad un piano verticale tangente al bordo dell'ombrello nel punto di distacco.
Proiettando il moto della goccia su di un asse verticale vale la relazione:
h = (1/2)*g*t^2
dove:
t = tempo di caduta al suolo
g = 9,80665 m/s^2 = accelerazione di gravità (val. standard)
Perciò la goccia cade a terra dopo un tempo pari a:
t = sqrt(2*h/g) (1)
Proiettando invece il moto lungo un asse orizzontale appartenente al piano della traiettoria vale la relazione del moto rettilineo uniforme:
v = d/t (2)
dove:
v = componente orizzontale della velocità della goccia
d = sqrt(R^2 – r^2) = distanza orizzontale percorsa nel tempo di caduta t
Dalla combinazione di (1) e (2) si ha:
v = sqrt(g*(R^2 – r^2)/(2*h)) = 2,077 m/s
Poiché v è costante, essa coincide con la velocità iniziale della goccia al momento del distacco, cioè coincide con la velocità periferica dell'ombrello, il quale percorrerà un giro completo in un tempo T pari a:
T = 2*pigreco*r/v = 2,117 secondi
La motivazione (file .pdf) di Vinciprova Francesco
Due monete
|
|
Due monete
Due monete da un euro sono poste come in figura. Dopo un giro completo della moneta superiore intorno a quella inferiore in quale posizione si verrà a trovare la moneta superiore? |
Vinciprova Francesco – leggi la soluzione (.pdf)
Alfredo Costa – Leggi la soluzione (.pdf)
Ciliegina
|
|
Una ciliegina nel cocktail
In un bicchiere da cocktail conico c'è una ciliegina sferica e del liquore che ricopre esattamente la ciliegina, come in figura. Sapendo che il raggio della ciliegina è 1 cm e che l'altezza del liquore è 6 cm, calcolare la quantità di liquore. |
Il volume di liquore è 5/3 * pi_greco cm^3
La motivazione di Neper (Reggio Calabria):
Facciamo riferimento alla figura che si ottiene come sezione di un piano perpendicolare all’asse del bicchiere.
I triangoli ottenuti sono simili, pertanto si avrà: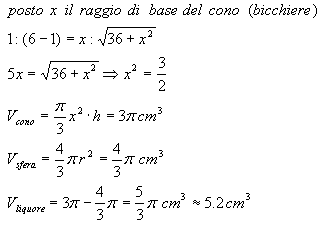
Campagna pubblicitaria
 |
Una campagna pubblicitaria
Un'agenzia pubblicitaria vuole pianificare la campagna di un certo prodotto servendosi dei seguenti tre canali: televisione, radio, riviste illustrate. Essa deve decidere quanti comunicati commerciali assegnare ad ogni canale per raggiungere il massimo numero possibile di potenziali consumatori, rispettando certi vincoli di budget. Nella tabella che segue sono indicati i costi relativi ad ogni canale e il numero di potenziali consumatori (complessivi o soltanto donne) raggiunti con un comunicato commerciale diffuso sui tre canali.
La campagna prevede un investimento di 420.000 € e questa somma non può essere superata; anzi, se possibile, deve essere spesa esattamente. Inoltre, vi vuole che Determina il numero ottimale di comunicati da diffondere su ogni canale. |
I comunicati da trasmettere sono: 30 per televisione, 50 per radio, 30 su riviste.
La motivazione di Pontormo (Reggio emilia):
Indichiamo con a, b, c il numero di comunicati via Tv, radio, riviste rispettivamente.
Cercheremo innanzitutto di studiare il caso in cui la somma viene interamente spesa, ossia il caso in cui
7.000a + 3.000b + 2.000c = 420.000 (*)
Le varie condizioni possono essere così espresse:
1. il numero di donne deve essere almeno di 20.000.000
300.000a + 200.000b + 100.000c >= 20.000.000
2. la spesa in pubblicità televisiva non deve superare la metà del totale
7.000a <= 210.000
3. i vincoli sul numero di comunicati
a >= 10 ; b >= 20 ; c >= 30
Posti tali vincoli, si deve cercare di ottenere il massimo numero di contatti; ciò significa trovare il massimo della funzione
f = 900.000a + 375.000b + 150.000c
Da (*) si ha c = (420 – 7a – 3b)/2; sostituendo e semplificando si ha il seguente sistema di disequazioni a due incognite:
a >= 10
b >= 20
a <= 30
7a + 3b <= 360
a – b <= 20
coniugato alla funzione da massimizzare f = 375.000a + 150.000b + 31.500.000
Si tratta di un classico problema di programmazione lineare risolvibile con metodo grafico.
La zona ammissibile sul sistema di assi cartesiani (a,b) é un trapezio delimitato dai punti P(10,20); Q(30,20), R(30,50) e S(10,290/3). Il massimo della funzione f si ha sul vertice R.
Pertanto a = 30, b = 50, c = (420 – 7*30 – 3*50)/2 = 30 e
f = 375.000*30 + 150.000*50 + 31.500.000 = 50.250.000.
Nel caso in cui non si spenda tutto, il problema é analogo; la funzione da massimizzare é una retta parallela ad f con intercetta dell'asse b inferiore a quella di f; pertanto i valori che si ottengono sono inferiori a quelli ottenuti prima. In conclusione la soluzione ottimale é quella ottenuta in precedenza.
La motivazione di Giancod (Roma):
Infatti il rapporto "costo/potenziali consumatori" più conveniente è quello della tv, poi viene la radio ed infine le riviste.
Per ottenere il massimo numero di consumatori converrà allora mandare per tv il massimo numero di messaggi, che è 30, perchè la spesa per la tv non deve superare 210.000 E (30 x 7000 = 210.000).
A questo punto conviene mandare il massimo numero di messaggi per radio, che è 50, poichè almeno 30 messaggi devono essere affidati alle riviste ( (210.000 – (2000×30)) / 3000 = 50).
A questo punto non resta che verifificare che anche l'ultim condizione sia soddisfatta e cioè il numero di donne raggiunte superi i 20.000.000:
300.00×30+200.000×50+100.000×30 = 22.000.000.
Irrigazione
|
|
Un giardino da innaffiare
Un giardino rettangolare di dimensioni 100m x 150m, deve essere irrigato con degli irrigatori a pioggia. Ciascun irrigatore innaffia una regione circolare di 10m di raggio. Qual è il minimo numero di irrigatori necessario per innaffiare direttamente ogni punto del giardino? |
Pasquale Salemme
Siano x e y due assi cartesiani rispettivamente lungo la dimensione corta (100 m) e lungo la dimensione lunga (150 m) del rettangolo.
Per una copertura completa del giardino si può far riferimento alla figura geometrica elementare dell'esagono regolare, ripetendo la quale si può coprire il rettangolo giardino in modo uniforme a forma di tassellatura come la pavimentazione di una stanza con mattonelle esagonali. Con questa tipo di copertura si viene a ridurre al minimo le zone di sovrapposizione dei cerchi descritti dagli irrigatori.
La superficie del giardino viene suddivisa in poligoni regolari esagonali di lato 10 m, contigui, incastrati fra di loro a reticolo.
Nel file allegato excel (foglio 1) :Gioco_15 nelle colonne B e C sono riportati le coordinate dei centri dei cerchi circoscritti agli esagoni regolari di raggio 10 metri.
Per coprire la superficie del giardino rettangolare di dimensioni 100×150 metri sono necessari 66 esagoni, nei cui centri si posizionano 66 irrigatori.
Dal suddetto file excel (grafici 1, 2, 3) si osserva:
Nel grafico 1:
sono riportati in scala le posizioni dei 66 irrigatori. Si nota che gli ultimi 3 irrigatori (n. 64-65-66) sono posizionati fuori del rettangolo per coprire solo una piccola zona all´interno del rettangolo.
Nel grafico 2:
viene evidenziata la parte del rettangolo differenza tra l´intero rettangolo e la zona coperta dei primi 59 irrigatori.
Questa zona dovrebbe essere coperta dagli ultimi 7 irrigatori (dal n. 60 al n. 66).
Con opportuni calcoli eseguiti nel foglio 1 del file excel (colonne E e F in colore rosso) si sono calcolate le coordinate
della posizione di 6 irrigatori tali da coprire la zona di giardino suddetta riducendo da 7 a 6 il numero di irrigatori necessari, per un totale di 65 irrigatori.
Nel grafico 3:
Sono stati evidenziati tutti i 65 irrigatori in particolare gli ultimi 6, numerati da 60 a 65. Inoltre, dando nelle caselle H1 e I1 del foglio 1, le coordinate
x , y di un punto qualsiasi appartenente al rettangolo, si può leggere nella colonna J le distanze di tale punto da tutti i centri e in colonna L, in corrispondenza del SI della colonna K, a quale o a quali cerchi il punto considerato appartiene.
Brioschi Marco Attilio
Come si può vedere nel file Excel allegato , foglio "Sovrapposizione", ho cercato innanzitutto di posizionare gli irrigatori in maniera che non vengano lasciati spazi non bagnati, quindi con le circonferenze di cerchi contigui tangenti in un unico punto, che ho chiamato nel file Excel P.
La configurazione che minimizza la sovrapposizione delle aree e quindi consente localmente di ottimizzare il numero di irrigatori e' quella per cui i centri si trovano a distanza RAD (3)*R gli uni dagli altri, cioe' a 17.32m di distanza. Con tale valore infatti un'area pari a 54.352 m2 (il 5.7669 % del totale delle aree dei 3 cerchi) e' bagnata da piu' di un irrigatore, mentre con distanze minori o maggiori tra i centri, si ottiene una percentuale maggiore.
Questa geometria localmente ottimale, sarebbe quella da utilizzare nel caso l'area da bagnare fosse di grandi dimensioni (in teoria infinita), perche'
lo spazio risparmiato minimizzando le sovrapposizioni localmente porterebbe sicuramente a minimizzare anche il numero degli irrigatori.
Tuttavia avendo l'area del giardino dimensioni finite, 100m x 150m, puo' darsi che configurazioni meno ottimizzate localmente, lo siano invece
globalmente.
La minima configurazione si trova infatti con il disegno allegato nel file Excel, foglio "Soluzione", utilizzando 65 irrigatori i cui centri sono
distanziati in verticale di 16.67m (cioe' 100m/6) ed in orizzontale di 15.53m. Gli irrigatori sono allineati in senso verticale e formano 5 file di
6 irrigatori e 5 file di 7 irrigatori.
Fuortes Antonio
rettangolo di base 150 m e altezza 100 m; raggio irrigazione 10 m disposizione suggerita:
(non riesco a inverntarne una migliore)
…..o…….o…….o…….o…….o.
.o…….o…….o…….o…….o…..
…..o…….o…….o…….o…….o.
.o…….o…….o…….o…….o…..
…..o…….o…….o…….o…….o.
.o…….o…….o…….o…….o…..
…..o…….o…….o…….o…….o.
.o…….o…….o…….o…….o…..
…..o…….o…….o…….o…….o.
.o…….o…….o…….o…….o…..
…..o…….o…….o…….o…….o.
.o…….o…….o…….o…….o…..
…..o…….o…….o…….o…….o.
una delle possibili soluzioni,
ecco come disegnarla in Basic :
r=10 ' raggio di irrigazione
xColo1=.543*r ' ascissa della prima col.
dx=1.546*r ' passo tra le colonne
maxColo=10 ' numero delle colonne
yRiga1=-0.04*r ' ordin. della prima riga
dy=.834*r ' passo tra le righe
maxRiga=13 ' numero delle righe
' ascisse delle col.=xColo1, xColo1+dx,
' xColo1+2*dx, …, xColo1+(maxColo-1)*dx
' ordinate delle righe=yRiga1, yRiga1+dy,
' yRiga1+2*dy, …, yRiga1+(maxRiga-1)*dy
screen 12: cls ' clear screen
window (-20,-20)-(170,120) ' 20 ai margini
line (0,0)-(150,100),,B ' box del campo
nUgelli=0
for Riga = 1 to maxRiga
yc=yRiga1+(Riga-1)*dy ' y del centro
for Colo = 1 to maxColo
xc=xColo1+(Colo-1)*dx ' x del centro
if (Riga+Colo) mod 2=1 then ' sulle righe dispari
circle (xc, yc), r ' i cerchi hanno centro
nUgelli=nUgelli+1 ' solo sulle col. pari,
end if ' e viceversa.
next Colo
next Riga
print "n=";nUgelli
' il numero totale di ugelli è 65.
arrivo a questo risultato in 3 fasi.
FASE 1:
copro il piano con una rete di triangoli equil. di base orizz. e
lato sqr(3)*10 m, con un irrigatore in ogni nodo (i cerchi si
toccano nel baric. di ogni triangolo);
noto che n righe di irrigatori coprono una fascia di 2*0.5*r+(n-1)*1.5*r di
altezza; quindi con 7 righe posso coprire esattamente l'altezza del campo,
ponendo i centri della prima riga a 5 m dal bordo inf. del campo, poi a 20,
35, 50, 65, 80, 95 m
noto poi che n col. coprono una fascia di (n-1)*r*sqr(3)/2 di larghezza;
quindi con 19 col. posso coprire con buon margine la larghezza del campo,
(fino a 155.88 m), ponendo i centri della prima col. (solo sulle righe 2,
4, 6) sul bordo sin. del campo, poi, seconda col., (solo sulle righe 1, 3,
5, 7) a 8.66 m dal bordo sin., etc, alternando le col. pari e dispari.
ecco come disegnarlo in Basic:
r=10 ' raggio di irrigazione
xColo1=0 ' ascissa della prima col.
dx=.866*r ' passo tra le colonne
maxColo=19 ' numero delle colonne
yRiga1=.5*r ' ordin. della prima riga
dy=1.5*r ' passo tra le righe
maxRiga=7 ' numero delle righe
… stesso programma come sopra
si vede che il numero totale di ugelli è 66, dato che le 7 righe si
realizzano in 2 col. adiacenti.
FASE 2:
tento ora la copertura del piano con una rete di triangoli equil. identici
ai preced., ma con un lato vert.;
noto che n col. di irrigatori coprono una fascia di 2*0.5*r+(n-1)*1.5*r
di larghezza; quindi con 11 col. posso coprire abbondantemente la larghezza
del campo (fino a 160 m), ponendo i centri della prima col. a 5 m dal bordo
sin. del campo, poi a 20, 35, 50, 65, 80, 95, 110, 125, 140, 155 m
noto poi che n righe coprono una fascia di (n-1)*r*sqr(3)/2 di altezza;
quindi con 13 righe posso coprire con buon margine l'altezza del campo,
(fino a 103.92 m), ponendo i centri della prima riga (solo sulle col. 2,
4, 6, 8, 10) sul bordo inf. del campo, poi, seconda riga, (solo sulle
col. 1, 3, 5, 7, 9, 11) a 8.66 m dal bordo inf., etc, alternando
le righe pari e dispari.
ecco come disegnarlo in Basic:
r=10 ' raggio di irrigazione
xColo1=.5*r ' ascissa della prima col.
dx=1.5*r ' passo tra le colonne
maxColo=11 ' numero delle colonne
yRiga1=0 ' ordin. della prima riga
dy=.866*r ' passo tra le righe
maxRiga=13 ' numero delle righe
… stesso programma come sopra
(anche qui sulle righe dispari i cerchi hanno centro solo sulle col.
pari, e viceversa).
il numero totale di ugelli è 71, peggiorando la situazione.
FASE 3:
deformo ora gradualmente la rete di triangoli che diventano isosceli:
ne accorcio la base (vert.) e ne allungo l'altezza (orizz.); le fasce
orizz. si stringono, il margine di copertura in altezza diminuisce, ma
aumenta quello in larghezza, fino a "cacciar fuori" dal campo, rendendola
inutile, la col. di destra.
ciò avviene quando la lungh. della base vert. dei triangoli scende tra
2*8.381 e 2*8,333 m
il programma e il disegno sono quelli in testa.
Ercole Suppa Scarica il file
Ruote cinghia
|
|
Ruote
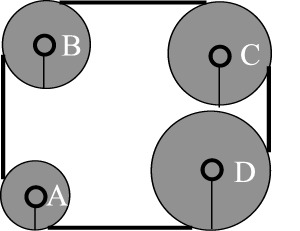
Quattro ruote A, B, C, D sono collegate tramite una cinghia e hanno rispettivamente raggi 14,15,16 e 18. Sono disposte come in figura in modo che il sistema sia libero di ruotare senza che la cinghia possa slittare. Dopo quanti giri della ruota A il sistema torna per la prima volta nella posizione iniziale? |
360 giri
La motivazione di Francesco Boano
Affinchè il sistema torni alla posizione iniziale le 4 ruote devono percorrere un "percorso" che sia multiplo di tutte e quattro.
Il percorso sarà quindi il minimo comune multiplo tra i "percorsi".
14 = 2 * 7
15 = 3 * 5
16 = 2^4
18 = 3^2 * 2
il percorso sarà quindi (2pi) ( 5 * 7 * 9 * 16)
e il numero di giri compiuti da A sarà (5 * 7 * 9 * 16) / 14 = 360
La motivazione di Aurelio Mascheroni
Ra, Rb, Rc, Rd -> raggi delle 4 ruote
x -> numero incognito di giri della ruota A
Dopo che A ruota di 1 giro, la cinghia trasla di 2*PIgreco*Ra e le altre ruote ruotano di un numero di giri dato rispettivamente da:
B -> 2*PIgreco*Ra /2*PIgreco*Rb = Ra/Rb
C -> Ra/Rc
D -> Ra/Rd,
poiché- in assenza di strisciamento- ciascuna ruota compie un numero di giri corrispondente al rapporto fra la lunghezza dell'arco di cui ha ruotato (eguale alla traslazione della cinghia) e quella dell'arco che corrisponde ad 1 giro completo.
Con i valori assegnati, dopo x giri di A le altre ruote ruotano di:
Nb= x*14/15
Nc= x*14/16= x*7/8
Nd= x*14/18= x*7/9
Affinché il sistema torni per la prima volta nella posizione iniziale, x deve rendere Na, Nb, Nc i più piccoli interi che soddisfano a tali equazioni.
Ciò porta alla ricerca del mcm dei denominatori delle 3 frazioni:
x = mcm (15, 8, 9) = 360
Per tale numero di giri di A si ottiene:
Nb= 336
Nc= 315
Nd= 280.
Scontrino esagerato
|
|
Uno scontrino esagerato Lo scontrino fiscale della cartoleria Cartesio è apparentemente esagerato. In realtà, spiega il cassiere, il registratore fiscale ha il difetto di non stampare un numero, anche se lo conteggia regolarmente. Il totale però è corretto. Qual è questo numero e quali sono i costi dei tre libri acquistati? Le risposte da inviare sono quindi Confronta la risposta |
Vanno eliminate le cifre 0, 1, 4 perché compaiono nello scontrino. Le soluzioni possibili sono tante
300+10300+133400, cifra mancante 3;
300+130300+13400, cifra mancante 3;
66600+61000+16400, cifra mancante 6;
66600+16000+64000, cifra mancante 6;
Chi sono questi matematici
Chi sono questi matematici?
 |
 |
 |
 |
|
1 |
2 | 3 | 4 |
 |
 |
 |
 |
| 5 | 6 | 7 | 8 |
 |
 |
 |
 |
| 9 | 10 | 11 | 12 |
 |
 |
 |
 |
| 13 | 14 | 15 | 16 |
 |
 |
 |
 |
| 17 | 18 | 19 | 20 |
Li hai riconosciuti tutti? E' un po' difficile, forse hai scoperto il trucco? Controlla la risposta
I matematici sono
-
Georg Cantor
-
René Descartes
-
Leonhard Euler
-
Galileo Galilei
-
Carl Friedrich Gauss
-
Charles Hermite
-
Christian Felix Klein
-
Luigi Lagrange
-
Pierre Simon de Laplace
-
Marius Sophus Lie
-
Isaac Newton
-
Jules Henri Poincaré
-
Bernhard Riemann
-
Bertrand Russell
-
James Joseph Sylvester
-
Evangelista Torricelli
-
Vito Volterra
-
Karl Weierstrass
-
David Hilbert
-
Kurt Goedel
Non c'e bisogno di consultare l'enciclopedia basta cliccare con il tasto destro del mouse e chiedere le proprietà dell'immagine
Maya
Immagine tratta da http://crystalinks.com/may.html , |
I calendari Maya I Maya avevano una grande paura che il tempo potesse finire e temevano grandi catastrofi in coincidenza con date particolari. Avevano numerosi calendari per misurare il tempo: tra i più importanti, l'Haab di 365 giorni approssimava l'anno solare, lo Tzolkin di 260 giorni rispondeva ad esigenze di tipo religioso. Il giorno della coincidenza della fine dei due calendari offrivano agli dei diversi sacrifici per far accettare loro il peso dei giorni a venire. Un po' come la nostra ossessione per la fine del millennio. Ma vista la fine della loro grande civiltà bisogna ammettere che le loro paure erano motivate. |
La soluzione è data dal più piccolo multiplo di 260 e 365, ossia il m.c.m. tra i due numeri:
5*22 *13*73=18980.
Oppure si può dividere il loro prodotto 260*365=94900 per il M.C.D che è 5:
94900:5=18980
Quindi 18.980 giorni, ossia 52 anni del calendario Haab e 73 anni del calendario Tzolkin.
Ciascun calendario ricomincia da capo dopo ogni multiplo del numero dei giorni
| 260 | 365 |
| 520 | 1270 |
| 780 | 1095 |
| 1040 | 1460 |
| 1300 | …. |
| … | …. |
| … | 18980 |
| … | |
| 18980 |
Infine la motivazione di MATRIX . Indichiamo con n il numero di anni da 365 giorni e con (n+m) il numero di anni da 260 giorni (n ed m sono naturali). La fine dei due anni coincidono quando 365n=260(n+m), cioè quando m/n=21/52 (irriducibile). Essendo n ed m numeri naturali, i due anni finiscono lo stesso giorno dopo che sono trascorsi 52 anni di 365 giorni e 52+21=73 anni di 260 giorni.
Campo
|
|
Il campo Un campo ha la forma di un poligono (chiuso). I suoi lati misurano 40m 50m 60m 70m 80m 90m 100m 110m Ogni lato è perpendicolare al lato precedente e a quello seguente. Individua una delle possibile forme del campo. Tieni presente che le misure indicate non sono di lati consecutivi. |
Le soluzioni sono tantissime.
La più elegante
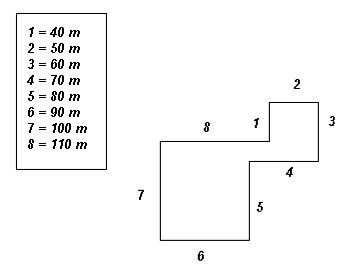soluzione di Bramanca (Lucca)
 |
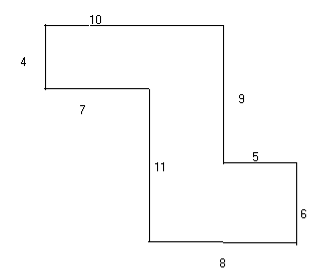Karpov è partito da un quadrato di lato 15 e accoppiando i lati a due a due 11+4, 10+5, 9+6, 8+7, ottenendo il disegno |
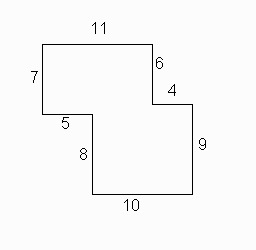Soluzione di Max
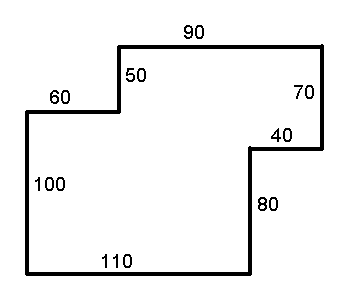Soluzione di Rodon
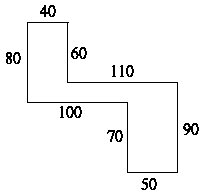Soluzione di Talos
Soluzione di Dodos
Fiormac ha dato la seguente soluzione. La somma dei lati è di m. 600.
E' sufficiente tracciare un quadrato di lato 150, dal quale "ritagliare", in due angoli opposti, due rettangoli con lati pari alle misure inferiori, ad es. 40×50 e 60×70, oppure 40×80 e 50×60.
Lozio ha dato la seguente soluzione. Divise per semplicità le misure delle lunghezze dei lati per 10, fissata un'origine P0 del disegno, assumiamo come positive le misure dei lati del poligono tracciati verso destra e verso il basso, negative quelle in verso opposto.
Con la convenzione assunta per i segni, il poligono risulta chiuso se le somme algebriche delle misure delle lunghezze dei lati orizzontali e verticali sono entrambe nulle.
Dato che ogni lato è perpendicolare al precedente, quattro lati devono risultare orizzontali e quattro verticali.
Divisi quindi gli otto valori (4…..11) in due gruppi di quattro, ciascuno relativo alle misure dei lati orizzontali (Oi) e verticali (Vi) rispettivamente, deve essere:
O1+O2+O3+O4=0 (1)
V1+V2+V3+V4=0 (2)
Dato che anche la lunghezza del lato maggiore (11) risulta < della somma dei tre minori, la (1) e la (2) possono essere soddisfatte solo con Oi e Vi a due a due di segno opposto. In particolare due quadruple sono ad esempio:
O1=9; O2=6; O3=-7; O4=-8
V1=4; V2=11; V3=-10; V4=-5.
Gallerista
 |
Il gallerista Il gallerista De Furbetti ha comprato per 2.500 euro due opere di un noto artista. Il giorno dopo le ha già vendute: una a 1.500 euro e l'altra a 1.700 euro. Qualche giorno dopo, gli telefona il collezionista De Tardetti che è disposto a pagare 5.000 euro per le due opere. De Furbetti riesce a riacquistare le due opere pagandole rispettivamente 2.000 e 2.500 euro. Quando si presenta il collezionista gli racconta tutta la storia, mostrando le varie ricevute: – Ho pagato i due quadri a 2.500 euro; li ho rivenduti a 1.500+1.700=3.200 euro: ho guadagnato 700 euro; li ho ricomprati a 2.000+2.500=4.500 euro: ci ho rimesso 1.300 euro; se te li rivendo a 5.000 euro, guadagno 500 euro ma in totale ci rimetto 100 euro. Se li vuoi mi devi far guadagnare almeno i 700 euro che avevo guadagnato con la prima vendita, quindi devi darmi altri 800 euro. A De Tardetti il discorso sembra corretto perciò gli dà 5.800 euro. In realtà, De Furbetti sa che le cose non stanno così. Quanto ha guadagnato complessivamente il gallerista? Dov'è l'imbroglio? |
 |
|
| Queste immagini sono di Giovanni Saini. Per vedere la sua produzione http://www.geocities.com/SoHo/Lofts/1758/index.html Il valore economico delle sue opere non ha nulla a che vedere con il testo del problema proposto. |
Prima di tutto facciamo i conti per bene poi scopriamo l'imbroglio.
Spese del gallerista: 2.500 + 2.000 + 2.500 = 7.000 euro
Incassi del gallerista: 1.500 + 1.700 + 5.800 = 9.000 euro
Guadagno: 9.000 – 7.000 = 2.000 euro.
Come ha spiegato Roberto (Roma) ,
l'imbroglio è nella frase " Se te li rivendo a 5.000 euro, guadagno 500 euro ma in totale ci rimetto 100 euro." Per onesta, avrebbe dovuto dire " Se te li rivendo a 5.000 euro, guadagno 500 euro ma avendo già guadagnato 700 euro …"
Luposaltellante (Termini Imerese)
l'ha spiegato in questo modo: L'imbroglio sta nel fatto che nell'acquisto da 4500 euro il capitale non è tutto del gallerista, infatti aveva gia guadagnato 700 euro dalla precedente vendita:solo 3800 euro era dunque la spesa sostenuta dal gallerista, per cui, rivendendoli a 5000 avrebbe guadagnato 1200 euro (e non rimesso 100).
Fiormaca (Molinella BO)
Si tratta di due distinte compravendite, non collegate seppure riguardanti la stessa merce. La prima si è già conclusa, con un guadagno di 700 euro; nella seconda, a fronte di un esborso di 4.500 euro, si ha un introito di 5.800 euro, con un guadagno di 1.300 euro.
X (Caltagirone CT)
Quando De Furbetti dice: "li ho ricomprati a 2.000+2.500=4.500 euro: ci ho rimesso 1.300 euro" non tiene conto dei 700 euro guadagnati in precedenza: l'imbroglio è proprio qui.
Barney (Catania)
ha formulato il ragionamento del gallerista con un'espressione algebrica:
Detti A1, A2, A3 e A4 gli importi (con segno) delle 4 operazioni effettuate, il guadagno totale (corretto) è dato da:
A1+A2+A3+A4 = -2500+3200-4500+5000=1200
Col ragionamento del gallerista invece sarebbe:
(A1+A2) + (A2+A3) + (A3+A4) = A1+2*A2+2*A3+A4 = -2500 + 2*3200 – 2*4500 + 5000 = -100
Franz Kafka (Carpi MO)
L'astuto de Furbetti ha in realtà conteggiato due volte le due transazioni (+3200-4500=-1300) con il seguente meccanismo:
-2500+3200 = +700 (utile della prima coppia di operazioni)
+3200-4500= – 1300 (perdita della seconda coppia di operazioni)
+5000-4500= + 500 (utile della terza coppia di operazioni, se il compratore pagasse i 5000 Euro concordati)
+800 = + 800 (sovrapprezzo chiesto al compratore)
La somma algebrica di queste operazioni, come si può notare, vale +700 Euro, ma le operazioni (+3200 e -4500) sono state conteggiate due volte!
Autobus
 |
Autobus Una società di trasporti deve collegare per mezzo di autobus la stazione con l'aeroporto di una città. Il percorso viene effettuato in 30 minuti; ogni autobus sosta 5 minuti alla stazione e 5 minuti all'aeroporto; ogni 10 minuti deve partire un autobus sia dalla stazione sia dall'aeroporto. |
|
|
|
 |
Qual è il minimo numero di autobus necessario? |
 |
||
Supponendo che il percorso richieda lo stesso tempo, ogni autobus impiega 30' (andata) + 5' (sosta) + 30' (ritorno) + 5' (sosta). In totale 70'. Volendo far partire un autobus ogni 10', occorrono 70:10=7 autobus.
Gli autobus non devono partire contemporaneamente dall'aeroporto e dalla stazione ma sfalsati di 5'.
Un'illustrazione di Barney (Catania)
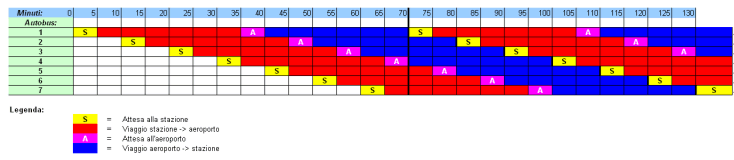
Una tabella dei tempi di Mgiacomello (Milano)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Partenza per Aeroporto | 10.00 | 10.10 | 10.20 | 10.30 | 10.40 | 10.50 | 11.00 |
| Arrivo Aeroporto | 10.30 | 10.40 | 10.50 | 11.00 | 11.10 | 11.20 | 11.30 |
| (Sosta) partenza per Stazione | 10.35 | 10.45 | 10.55 | 11.05 | 11.15 | 11.25 | 11.35 |
| Arrivo Stazione | 11.05 | 11.15 | 11.25 | 11.35 | 11.45 | 11.55 | 12.05 |
| (Sosta) partenza per Aeroporto | 11.10 | 11.20 | 11.30 | 11.40 | 11.50 | 12.00 | 12.10 |
Autobotte
 |
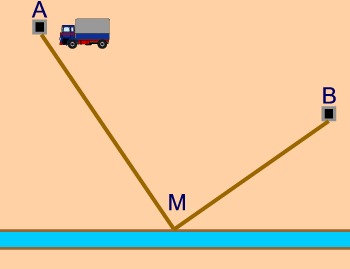Autobotte Un'autobotte deve riempire i pozzi A e B da un canale, come nel disegno. Parte da A riempie la botte dal canale, scarica l'acqua in B, ritorna al canale, riempie la botte e scarica l'acqua in A. Da quale punto M conviene che carichi l'acqua? Dare la soluzione con una costruzione geometrica. |
Matrix (Teramo)
Franz Kafka (Carpi)
Indichiamo con B' il punto simmetrico di B rispetto alla retta individuata dal canale. Deve essere minima la distanza complessiva AM+MB+BM+MA. Dato che B e B' sono simmetrici, in pratica deve essere minima la distanza AM+MB'. Tale distanza è minima quando i tre punti A, M, B' sono allineati.
Dunque dovrà essere AMC = C'MB', essendo due angoli opposti al vertice. Per simmetria dovrà quindi essere AMC=CMB. La posizione di M è quindi quella per la quale l'angolo di incidenza è uguale a quello di riflessione (È il principio di Fermat).
Cavia (Castelvetro MO)
Il punto M è quello …
1) … che divide il segmento delle proiezioni di A e B sulla retta del fiume in parti direttamente proporzionali alle distanze di A e B dal fiume;
2) … per il quale la perpendicolare per M alla retta del fiume è bisettrice dell'angolo AMB;
3) … che si ottiene congiungendo A con il simmetrico B' di B rispetto alla retta del fiume (retta della sponda del fiume dalla parte di A e B!)
Ucando (Gallarate VA)
Supponiamo di trasferire il problema in un asse cartesiano. I punti A, B, M hanno le coordinate:
A ( 0 ; Ya )
B ( Xb ; Yb)
M ( Xm, 0 )
La richiesta consiste nel minimizzare la somma di AM e BM; senza scrivere la formula con il teorema di Pitagora, indicherò con f(x) la funzione AM + BM. Occorre, per calcolare il punto di minimo di f(x), calcolare la derivata prima f ' (x) e porla = 0. Si arriva alla soluzione Xm= (Xb * Ya)/(Yb+Ya)
con Xm la nostra incognita (perchè si deve decidere in quale punto attingere acqua dal canale, e questo risiede sull'asse delle ascisse). E' da notare che il numeratore della soluzione (Xb * Ya) corrisponde
all'area del rettangolo circoscritto ai tre punti.
Emy e Max (Torino)
Secondo me si può risolvere (per tentativi) attraverso un'ellisse: prendiamo la classica corda i cui estremi fissiamo in A e B, il luogo dei punti ottenuti tendendo la corda con una matita è notoriamente un'ellisse; se la corda è troppo lunga, l'ellisse taglierà in due punti il canale; riducendo dunque la lunghezza della corda fino a quando la nuova ellisse è tangente al canale, individuo sia il punto M (è il punto di tangenza) che la distanza A-M-B (che è la lunghezza della corda).
Roberto (Roma)
| La soluzione viene rappresentata nella costruzione geometrica riportata nel disegno allegato. In esso si vede che il punto M è il punto di incrocio delle due diagonali del trapezio isoscele ABB'A' avente come asse di simmetria la retta CD rappresentativa del canale. Infatti il percorso minimo dell'autobotte è equivalente al segmento di linea retta AB' = AM + MB' = AM + MB in un verso e al segmento di linea retta BA' = BM + MA' = BM + MA nell'altro verso. |
 |
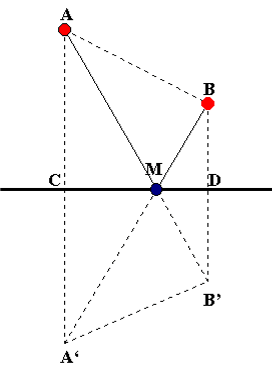Amelia (Milano)
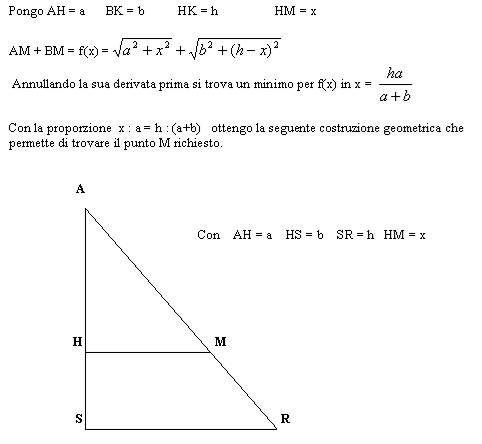
Sistema formale
 |
Sistema formale Un teorema è una stringa di lettere dell'alfabeto italiano. 1. In una stringa che contiene due lettere uguali affiancate si possono eliminare entrambi le lettere 2. In una stringa che contiene due vocali affiancate si può eliminare la seconda delle due vocali. 3. In una stringa che contiene due consonanti affiancate si può eliminare la seconda delle due consonanti. 4. In una stringa si può aggiungere l'intera stringa o una sua parte terminale composta da almeno due lettere. MATEMATICA è l'unico assioma del sistema, dimostrare il teorema MAMMA. Si tratta di trasformare la stringa MATEMATICA utilizzando le quattro regole fino a ottenere la stringa MAMMA. |
Come ha osservato Leon (Teramo) , si può prima dimostrare un LEMMA
Utilizzando le regole di inferenza ogni stringa di lunghezza n>=3, che termina con tre caratteri XYZ di tipo diverso (ossia vocale, consonante, vocale oppure consonante, vocale, consonante) può essere trasformata nella stringa di
lunghezza n-1 che si ottiene eliminando l'ultimo carattere.
DIMOSTRAZIONE.
…XYZ —-> (regola 4)
…XYZXYZ —-> (regola 2 o 3)
…XYZYZ —-> (regola 4)
…XYZYZZYZ —-> (regola 1)
…XYZYYZ —-> (regola 1)
…XYZZ —-> (regola 1)
…XY
TEOREMA.
Utilizzando le quattro regole si può trasformare la stringa MATEMATICA nella
parola MAMMA.
DIMOSTRAZIONE
Applicando 8 volte il LEMMA precedente, la stringa MATEMATICA si può
trasformare
nella stringa MA. Dalla stringa MA si può ottenere MAMMA nel modo seguente:
MA —-> (regola 4)
MAMA —-> (LEMMA)
MAM —-> (regola 4)
MAMMAM —-> (LEMMA)
MAMMA
Osservazioni curiose sono state fatte sulle parole che si ottengono nel corso della dimostrazione:
MATEMATICACCA non è certo un bel passaggio
MATETTE è già più interessante
per arrivare a sciogliere il dilemma MAMMA o non MAMMA?
Gotenx (Mori TN) mi ha fatto sapere che MA significa demonio in giapponese. Ha giustamente osservato che partito da MATEMATICA, ha capito MATEMATICACCA, poi è arrivato il demonio per punirlo ed infine la MAMMA lo ha salvato.
Strade
 |
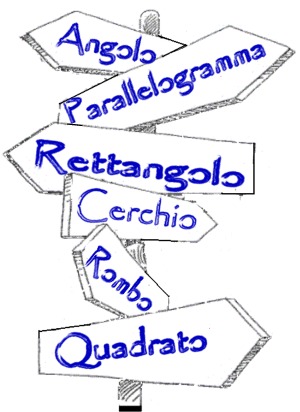Strade Nel paese della Geometria, le città hanno nomi geometrici. Sono collegate tra di loro dalle seguenti strade:
Quadrato è collegato a Equilatero E' possibile andare da Equilatero a Parabola? |
La relazione di collegamento suddivide l'insieme delle città in due sottoinsiemi disgiunti. Le città del primo sottoinsieme non sono collegate con quelle del secondo. Equilatero e Parabola appartengono a due sottoinsimi distinti.
Il disegno è di Leon (Teramo)
Quadratini
 |
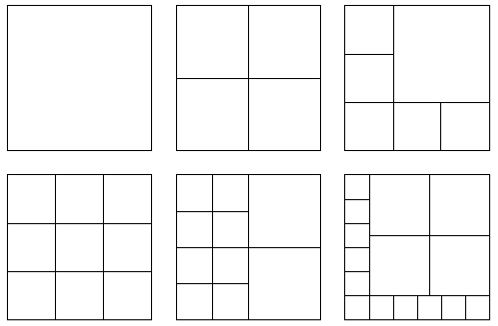Quadrati Un quadrato si può dividere in quadrati più piccoli. Nella figura un quadrato è stato diviso in 1, 4, 6, 9, 10, 15 quadratini. Sei in grado di costruire le suddivisioni in un numero di quadrati da 1 a 20? Puoi utilizzare le suddivisioni del disegno a fianco. Se non hai disponibile un programma di grafica puoi utilizzare un foglio word da inviare come allegato. |
La soluzione di Matrix Teramo
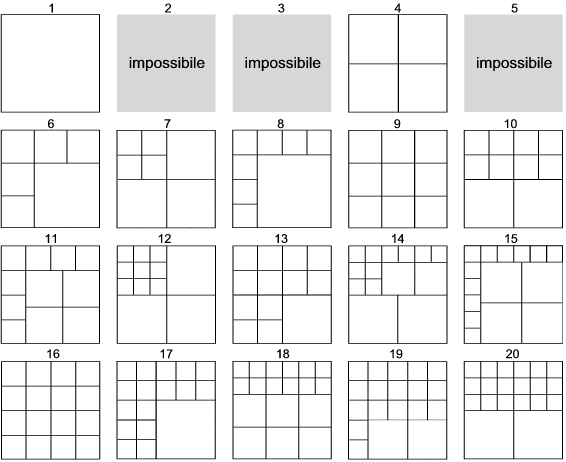
Le osservazioni di Franzkafka Carpi (MO)
Ho osservato che ogni volta che è possibile suddividere in n quadratini il quadrato dato, allora si può suddividerlo anche in n+3 quadratini. A partire dalle suddivisioni in 1, 6, 8 quadratini è possibile in questo modo ottenere le suddivisioni in qualsiasi numero di quadratini compreso fra 1 e 20, con l'eccezione di 2, 3, 5.
La soluzione di Ucando Gallarate (VA)
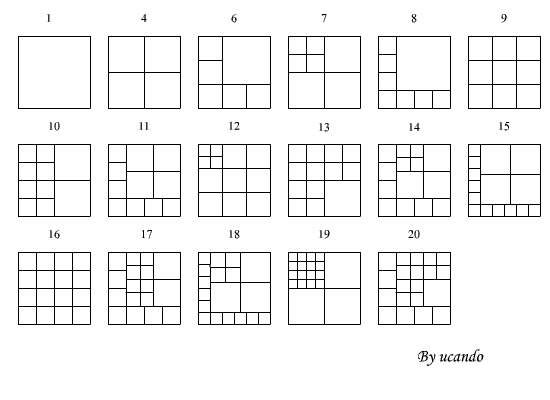
La risposta di Fibonacci Bogotà (Colombia)
I casi 2 e 3 sono impossibili:
dato che ci deve essere almeno un quadrato più piccolo, deve esserci almeno una linea che attraversi tutto il quadrato grande. Se ci fossero solo linee parallele ad essa, le figure semplicemente sarebbero rettangoli oblonghi e pertanto deve esserci, ad ogni lato di essa, una linea perpendicolare (ad essa). Contraddizione. Pertanto è impossibile.
Il caso 5 è impossibile anche se in questo momento non ne ho la prova.
Triangoli
Il complotto dei triangoli
Nel paese di Flatlandia , i triangoli appartengono alla casta inferiore, mentre i poligoni regolari alla nobiltà.
Un giorno, i 21 triangoli del disegno organizzano un complotto: si uniscono per formare un poligono regolare ed entrare nella casa di un nobile. Uno dei triangoli rimane fuori a fare il palo. Quale poligono regolare riescono a formare? Quale triangolo rimane a fare il palo?
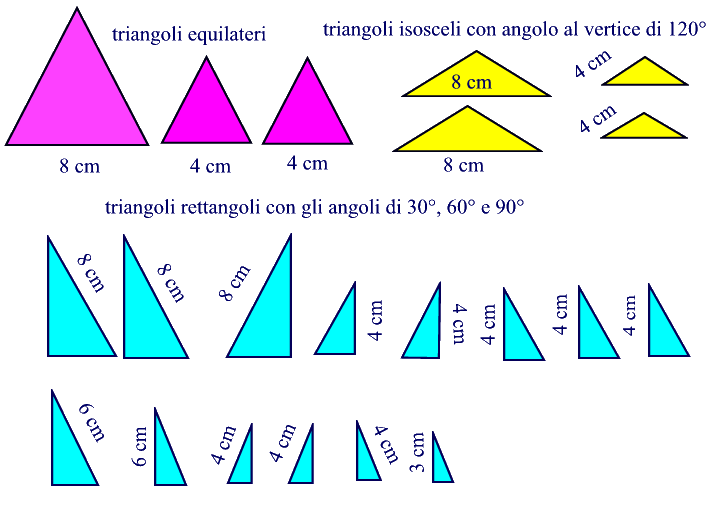
Costruito il poligono regolare? Trovato il palo? Confronta la tua soluzione con la mia
La prima osservazione è che gli angoli del triangolo sono di 30°, 60°, 90°, 120°. Con questi angoli non si può formare un poligono regolare con cinque angoli (pentagono) perché gli angoli di questo poligono misurano 108°; si può formare un esagono perché ha gli angoli di 120° gradi; non si può formare un poligono regolare con sette angoli perché gli angoli di questo poligono misurano 128°. Vi ricordate la formula per calcolare l’angolo interno di un poligono?
(numero di lati -2)*180°/ numero di lati.
Il poligono è quindi probabilmente un esagono di lato 8 cm. A questo punto si può verificare se l’area di questo poligono è inferiore rispetto alla somma delle aree di tutti i triangoli di una quantità che possa corrispondere a uno dei triangoli.
Per comporre l’esagono regolare occorre comporre 6 triangoli equilateri di lato 8 cm. Una possibilità è la seguente
-
triangolo1
-
triangoli 8 e 9
-
triangoli 3, 6, 10
-
triangoli 4, 5, 11, 12
-
triangoli 2, 7, 13, 14, 15
-
triangoli 16, 17, 18, 19, 21
Il triangolo escluso è il 20 con ipotenusa 4 cm.
Una conferma viene dal calcolo delle aree. L’area di un esagono regolare di 8cm di lato è data da
perimetro (8*6=48)*apotema(4*/3 )=166,277cm2
Sommando le aree di tutti i triangoli disegnati si ottiene una superficie di poco più grande, esattamente di 3,464cm2 che corrisponde all’area di un triangolo con angolo di 30°, 60° e 90° e ipotenusa 4cm.
Per calcolare le aree dei triangoli che hanno 30°, 60° e 90°, conoscendo un solo lato si applicano le seguenti formule:
l, ipotenusa, l/2 cateto più piccolo, (l/2)*/3 l’altezza.
Commessa
La commessa licenziata
|
|
La commessa di un negozio di musica è incaricata dal direttore di vendere una scatola di 300 CD al prezzo di 10.000 lire ogni 2 CD. Poco dopo il vicedirettore incarica la stessa commessa di vendere un'altra scatola di 300 CD della stessa marca ma al prezzo speciale di 10.000 lire ogni 3 CD. Completamente disorientata, la commessa non sa a quanto vendere i CD. Come fare a venderli a prezzo differente se i CD sono uguali? Decide allora di applicare la seguente offerta speciale: 5 CD a 20.000. In questo modo venderà 3 CD a 10.000 e 2 CD a 10.000, tenendo contenti entrambi i datori di lavoro. A fine giornata, dopo aver venduto tutti i CD, i conti non tornano. Il direttore pretende (300:2)x10.000=1.500.000. Il vicedirettore pretende (300:3)x10.000=1.000.000. In totale i due pretendono 2.500.000. La ragazza ha invece incassato (600:5)x 20.000 = 2.400.000. Viene accusata di aver rubato 100.000 dalla cassa e licenziata. Siete in grado di assumere la difesa 'matematica' della ragazza e dimostrare che non ha rubato bensì non ha saputo fare bene i calcoli? Dove ha sbagliato? Hai capito l'errore? Controlla la risposta |
L'errore è stato quello di aver venduto alcuni CD più costosi al prezzo di quelli meno costosi. Infatti, vendendoli 5 per volta ha esaurito prima quelli dell'offerta 3 a 10.000, esattamente dopo 100 vendite. A questo punto gli sono rimasti tutti quelli dell'offerta 2 a 10.000 che ha continuato a vendere al prezzo di 5 per 20.000, invece che 5 a 25.000, da qui la perdita di 100.000.
La commessa doveva vendere i Cd del primo gruppo a 5.000 lire l'uno e quelli del secondo gruppo a 3.333,3 lire l'uno, invece li ha venduti a 4.000 lire l'uno. Il prezzo medio per CD doveva essere 8333/2 = 4165, quindi 20.825 per ogni pacco da 5. Il calcolo corretto doveva essere
[(300/2)*10000 + (300/3)*10000)/600]*5=4166,6.
La media di 1/2 e 1/3 vale 5/12, secondo la commessa la media è 2/5.
Ancora (300/2 + 300/3)*10.000 non è la stessa cosa di (600/5)*20.000, è sostanzialmente lo stesso errore che si commette quando si sommano numeratore e denominatore della frazione.
VERDETTO della Giuria dei partecipanti al gioco: non colpevole.
La ragazza non è molto brava in matematica ma, come ha osservato L.De Luca, se è capace di vendere 600 CD in un giorno non è certo da licenziare:)
Ruote
|
|
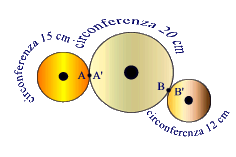
Ruote I tre dischi ruotano a stretto contatto e contemporaneamente. Il primo ha una circonferenza di 15 cm, il secondo di 20 cm, il terzo di 12 cm. |
N1 il numero di giri della prima ruota, N2 quello della seconda, N3 quello della terza. Deve valere la relazione
N1*15=N2*20=N3*12
da cui N1/N2=20/15, semplificando 4/3. I valori più piccoli per N1 e N2 sono appunto 4 e 3.
Come verifica N2/N3=12/20=3/5, quindi N2=3, N3=5.
In conclusione i punto A, A', B, B' tornano a coincidere dopo 3 giri della ruota centrale. La prima ruota compirà 4 giri, la terza 5 giri.
Dopo rispettivamente 4, 3 e 5 giri delle ruote
il punto A ha percorso 3*20cm=60cm
il punto A' ha percorso 4*15cm=60cm
il punto B ha percorso 3*20cm=60cm
il punto B' ha percorso 5*12cm=60cm.
Da ciò si deduce che è sufficiente calcolare il m.c.m. tra 15, 20, 12 che è 60: tutti e quattro i punti possono percorrere contemporaneamente 60 cm. La seconda ruota avrà fatto 60/20=3 giri.
Un altro modo per arrivare alla soluzione può essere la seguente:
dopo 1 giro le ruote hanno percorso rispettivamente cm 20, 15, 12
dopo 1 giro le ruote hanno percorso rispettivamente cm 40, 30, 24
dopo 1 giro le ruote hanno percorso rispettivamente cm 60 , 45, 36
dopo 1 giro le ruote hanno percorso rispettivamente cm 80, 60 , 48
dopo 1 giro le ruote hanno percorso rispettivamente cm 100, 75, 60
che sono i multipli di 20, 15, 12. &0 è il minimo comune multiplo.
Quadrati
 |
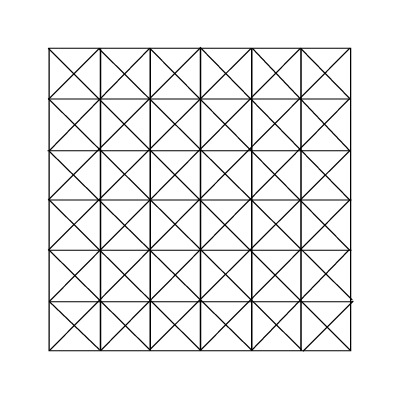Quanti quadrati ci sono nella figura?
Molti … |
Se ci si mette a contare a caso non si arriva da nessuna parte: i quadrati sono veramente tanti che è difficile contare a memoria.
Contiamo prima quelli disposti orizzontalmente.
I quadrati di lato 1 sono 6*6=36,
i quadrati di lato 2 sono 25, non dimenticate quelli centrali,
i quadrati di lato 3 sono 16,
i quadrati di lato 4 sono 9,
i quadrati di lato 5 sono 4,
infine 1 quadrato di lato 6.
91 quadrati orizzontali.
Ora quelli disposti in modo obliquo.
lato 1 quadrati 60
lato 2 quadrati 41
lato 3 quadrati 24
lato 4 quadrati 13
lato 5 quadrati 4
lato 6 quadrati 1
143 quadrati obliqui .
In totale 234 quadrati
Tesoro
|
|
Un tesoro! Tre ladri trovano un tesoro in una vecchia cassaforte. 21 preziose sfere in fine vetro di Murano, perfettamente saldate e sigillate. Al loro interno alcune contengono della polvere che sembra oro. Precisamente, 7 sono completamente piene di polvere d'oro, 7 piene per metà e 7 vuote. I tre vogliono dividersi il tesoro in parti uguali ma non vogliono danneggiare le sfere bucandole. Come possono fare per avere ognuno la stessa quantità di sfere, e la stessa quantità d'oro? Trovata la soluzione? Confrontala con la mia |
Uso i seguenti simboli: P sfera piena, p sfera semipiena, V sfera vuota
I risultati possibili sono
| 1° ladro | 3P | 1p | 3V | 3P | 1p | 3V | |
| 2° ladro | 3P | 1p | 3V | 2P | 3p | 2V | |
| 3° ladro | 1P | 5p | 1V | 2P | 3p | 2V |
Un po' di frazioni
Il riempimento delle sfere è dato da 7 + 7/2= 21/3, che diviso per 3 dà 7/2. Quindi ciascun ladro deve ricevere 7/2 d'oro. Le possibilità sono 0+7/2, 1+ 5/2, 2+3/2, 3+1/2.
La possibilità 0+7/2 è da escludere perché gli altri due ladri potrebbero al più ricevere 3+1/2 e 3+1/2, non accettabile perché in totale da 6+9/2.
La possibilità 1+5/2 può essere combinata con 3+1/2 e 3+1/2, in totale 7+7/2. E' la prima soluzione data.
La possibilità 2+3/2 non può essere combinata con 1+5/2, perché il totale delle mezze sfere dà 8/2.
La possibilità 2+3/2 può esser combinata con 2+3/2, al terzo toccherebbero 3+1/2. E' la seconda soluzione data.
Tennis
 |
Torneo di tennis In un torneo di tennis a eliminazione diretta solo i vincitori di ogni incontro giocano quello successivo, fino alla proclamazione del vincitore del torneo. Sapendo che in totale gli incontri sono stati 1023, quanti erano gli iscritti al torneo? Trovata la risposta? Confrontala con la nostra |
La risposta è 1024. Infatti, se sono stati fatti 1023 incontri significa che sono stati eliminati 1023 giocatori + 1 vincitore =1024.
1024 giocatori disputano 512 partite, ciascuna ha un vincitore, per cui al secondo turno partecipano in 524.
512 giocatori disputano 256 partite
256 giocatori disputano 128 partite
128 giocatori disputano 64 partite
64 giocatori disputano 32 partite
32 giocatori disputano 16 partite
16 giocatori disputano 8 partite
8 giocatori disputano 4 partite
4 giocatori disputano 2 partite
2 giocatori disputano 1 partita.
Osserva che 2, 4, 8, 16, 32, … sono le potenze di 2. Detto G il numero dei giocatori,
al primo turno si disputano G/2 incontri, al secondo G/4, al terzo G/8 ecc.
Quindi, al 1° turno G/21 , al 2° G/22 , al 3° G/23 , al 4° G/24 e così via nell'ultimo incontro I si ha G/2I , che deve essere uguale a 1. Da cui G/2I =1 => G=2I . Cioè i giocatori sono sempre una potenza di 2.
Luciano Sarra ha trovato l'occasione per introdurre anche la serie geometrica, riporto la parte finale della sua argomentazione, dove x=G, n=I
Bottoni
 |
Attacca bottoni Un unico filo celeste attraversa i buchi di un bottone. Quali dei dieci bottoni visti da dietro (R1 .. R10) NON corrispondono al bottone visto d'avanti? Trovati? Controlla la soluzione |
I bottoni R3 e R5 hanno il segmento di filo CD anche sul retro.
Clandestini
 |
Clandestini Tre bambini, immigrati clandestinamente, cercano un piccolo lavoro per sopravvivere. Vengono in contatto con un tipo losco che organizza le vendite di fazzoletti presso i semafori. Il tipaccio non vuole assolutamente prenderli a lavorare ma essi insistono di essere molto bravi e astuti. Alla fine, lo sfruttatore accetta ma alle seguenti assurde condizioni. |
| costo per pacco | 100 lire | 200 lire | 400 lire | totale |
| fazzoletti venduti dal primo | 30 | 15 | 5 | 8.000 |
| fazzoletti venduti dal secondo | 20 | 10 | 10 | 8.000 |
| fazzoletti venduti dal terzo | 10 | 5 | 15 | 8.000 |
Marte
 |
I marziani I marziani sono un popolo strano, lo sappiamo tutti. Hanno circondato l'equatore del loro pianeta con un lungo cavo per portare l'acqua. Ma il loro governatore non è contento: bisogna sollevare il cavo a 1 m di altezza, in modo che tutti possano passare comodamente di sotto. Di quanto gli ingegneri devono allungare il cavo? Fatto i calcoli? Controlla la soluzione |
Contrariamente a quanto si immagina a prima vista, non serve conoscere le dimensioni di Marte. Inoltre, il cavo va allungato di una quantità veramente modesta poco più di 6m, esattamente 2*PIGRECO m. Infatti, la lunghezza della circonferenza è data dalla formula 2*PG*R (PG = pigreco), aumentando R di 1 metro si ha
2*PG*(R+1) = 2*PG*R(circonferenza di Marte)+2*PG.
Faro
 |
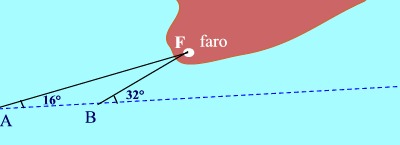Navigando per mare Una nave rileva, quando è nel punto A, un angolo di 16° tra la propria rotta e il faro F. Dopo un miglio è nel punto B e rileva una angolo di 32°. A che distanza si trova ora dal faro? In altre parole, qual è la distanza BF?
Pensaci su e verifica la tua soluzione |
L'angolo esterno a B vale 32°, quindi l'angolo interno vale 148°. Di conseguenza l'angolo F vale 18°. Ricorda il teorema secondo cui la somma degli angoli interni di un triangolo vale 180°. Oppure il teorema secondo cui un angolo esterno equivale allo somma dei due angoli interni non adiacenti ad esso.
In definitiva, il triangolo ABF è isoscele: AB = BF = 1miglio.
Quattro quattro
Quattro quattro
| Con quattro 4 e le quattro operazioni (+, -, *, /) ottenere come risultato i numeri interi da 0 a 10 |
Facile! |
0 = 44-44 = 4/4-4/4 = 4+4-4-4 = (4-4)/4/4 …
1 = 44/44 = 4-4+4/4 = (4+4-4)/4
2 = 4/4+4/4 =
3 = (4+4+4)/4 = (4*4-4)/4
4 = 4+(4-4)/4 = (4-4)*4 +4
5 = (4*4+4)/4
6 = 4+(4+4)/4 = (4+4)/4+4
7 = 4+4-4/4 = 44/4-4 =
8 = 4+4+4-4 = (4+4)*4/4 = 4*4-4-4 …
9 = 4+4+4/4
10=(44-4)/4
L’allenatore
L'allenatore
|
|
L'allenatore di una squadra di calcio deve decidere quale tattica adottare durante la partita. Sapendo che dovrà avere almeno un portiere, due difensori, due centrocampisti e un attaccante, qual è il numero totale di combinazioni tra cui scegliere? Ossia, quanti schemi di gioco (4,4,2 – 5,3,2) può ottenere? |
|
|
Trovata la soluzione. Vedi la mia |
| difensori | centrocampisti | attaccanti | |
| 2 | 2 | 6 | 1 |
| 3 | 2 | 5 | 2 |
| 2 | 3 | 5 | 3 |
| 3 | 3 | 4 | 4 |
| 3 | 4 | 3 | 5 |
| 4 | 3 | 3 | 6 |
| 4 | 2 | 4 | 7 |
| 2 | 4 | 4 | 8 |
| 4 | 4 | 3 | 9 |
| 5 | 2 | 3 | 10 |
| 5 | 3 | 2 | 11 |
| 5 | 4 | 1 | 12 |
| 2 | 5 | 3 | 13 |
| 3 | 5 | 2 | 14 |
| 4 | 5 | 1 | 15 |
| 6 | 2 | 3 | 16 |
| 6 | 3 | 1 | 17 |
| 2 | 6 | 2 | 18 |
| 3 | 6 | 1 | 19 |
| 2 | 7 | 1 | 20 |
| 7 | 2 | 1 | 21 |
1 portiere, 2 difensori, 2 centrocampisti e 1 attaccante sono obbligati, rimangono 5 altri giocatori da posizionare nei vari ruoli da aggiungere al modulo 1,2,2,1.
Borsa
Speculazioni in borsa
 |
La società di analisi statistiche matematicamente S.p.A. è quotata in borsa. Da diverso tempo le sue azioni sono in un fase laterale, ossia salgono e scendono restando in una banda di valori tra i 9 e gli 11 euro. Dopo un lungo periodo di osservazione si è notato il seguente comportamento regolare. 1. Se un giorno supera 10.5E, il giorno dopo perde il 10%. 2. Se un giorno scende sotto 10E, il giorno dopo sale del 10%. 3. Se un giorno aumenta del 10%, il giorno dopo scende del 5%. 4. Se un giorno scende del 10%, il giorno dopo sale del 5%. Ieri ha chiuso a 11E. Potendo eseguire un'unica operazione di acquisto e una di vendita nelle seguenti 30 giornate di borsa, e supponendo che i prezzi di chiusura siano identici a quelli di apertura, qual è l'operazione che dà il massimo guadagno? Indicare in quale dei trenta giorni conviene comprare, in quale vendere e quanto si riesce a guadagnare. Attenzione, nel caso in cui si possono applicare più regole, si applica quella che è espressa da un numero minore. |
|
Trovata la soluzione? Confrontala con la mia |
|
Con un foglio EXCEL si trovano i seguenti valori di apertura per ogni giornata di borsa.
Se si può vendere allo scoperto, si vende a 10,93 e si riacquista a 9,45 , guadagnando 1,48 Euro.
Se non sono ammesse le vendite allo scoperto , si compra a 9,50 e si vende a 10,93 , guadagnando 1,42 Euro.
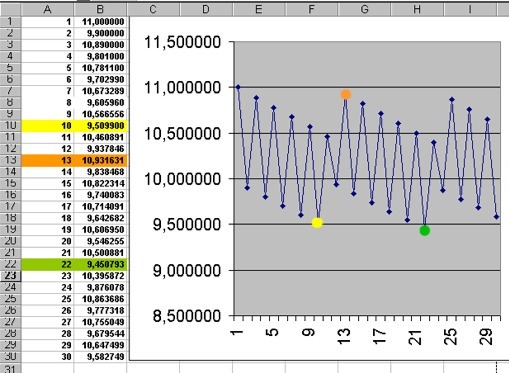
La tabella in Excel è stata ottenuta in questo modo.
Nella colonna A ho inserito i giorni. A1=1, A2=A1+1, quindi copia e incolla fino ad A30.
Nella colonna B ho inserito il valore in euro. B1=11, B2=B1*0,9 (per la condizione 1).
Nella casella B3 la formula =SE(B2>10,5;0,9*B2;SE(B2<10;1,1*B2;SE(B2=B1*1,1;B2*0,95;SE(B2=0,9*B1;1,05*B2;))))
che ho copiato fino a B30.
Il ragno e la mosca
Il ragno e la mosca
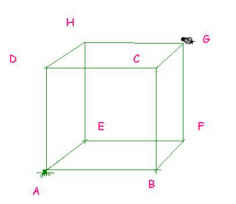
Un ragno ha costruito una ragnatela a forma di cubo.
Si trova nel punto A, quando una mosca si impiglia nel punto G.
Quanti sono i percorsi possibili per andare a A a G senza che nello stesso percorso ripassi due volte per lo stesso punto?
Indicare i percorsi possibili in questo modo
ABFG
ABFEHDCG
……
Fate attenzione a organizzare il vostro procedimento, altrimenti non sarete mai sicuri di aver ottenuto tutti i percorsi possibili.
Pensi di aver trovato la soluzione? Controllala
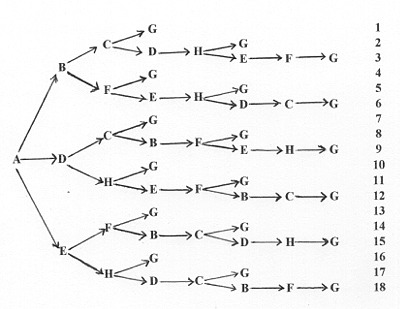
Quadrati e triangoli
 |
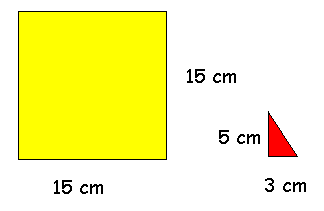Quadrati e triangoli Quante volte il triangolo rosso entra nel quadrato giallo? Trovata la soluzione? Controlla |
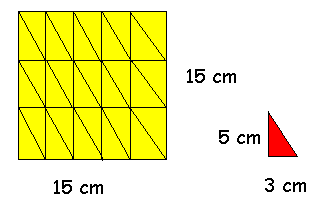
E' sufficiente calcolare l'are del quadrato 15*15=225 e l'area del triangolo 15/2. 225:15/2=30.
$int (arcsin (x))(xdx/sqrt(1-x^2))$
Integrale per parti
$int (arcsin (x))(xdx/sqrt(1-x^2))$
$intln(x+sqrt(1+x^2))dx=x*ln(x+sqrt(1+x^2))-intx/(sqrt(1+x^2))dx$
cioè
$x*ln(x+sqrt(1+x^2))-sqrt(1+x^2)+K$
FINE