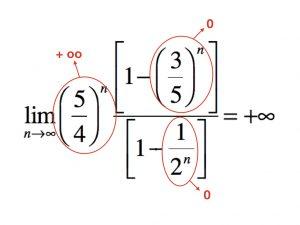
Il limite si presenta in una forma del tipo $ 1^(+oo) $, che è una forma indeterminata, anche se potrebbe non sembrarlo; per risolvere il limite, quindi, possiamo procedere scomponendo la successione in diversi fattori, applicando le proprietà delle potenze:
$ ( 1 + frac(1)(n^3) )^(πn^3 + n + 1) = ( 1 + frac(1)(n^3) )^(πn^3) * ( 1 + frac(1)(n^3) )^n * ( 1 + frac(1)(n^3) )^1 $
In questo modo, possiamo applicare il limite notevole seguente:
$ lim_(n to +oo) ( 1 + frac(1)(n^k) )^(n^k) = e $
Analizziamo ogni singolo fattore, cominciando dal primo:
$ ( 1 + frac(1)(n^3) )^(πn^3) $
Possiamo notare che il fattore può essere scritto in una forma equivalente applicando le proprietà degli esponenti delle potenze:
$ ( 1 + frac(1)(n^3) )^(πn^3) = [( 1 + frac(1)(n^3) )^(n^3)]^π $
In questo modo è possibile applicare il limite precedente considerando $k = 3$; per le proprietà dell’algebra dei limiti, possiamo applicare il limite alla funzione dentro parentesi quadre, ed elevare poi l’intero limite a $π$ :
$ lim_(n to +oo) [( 1 + frac(1)(n^3) )^(n^3)]^π = $
$ [ lim_(n to +oo) ( 1 + frac(1)(n^3) )^(n^3) ]^π = [e]^k = e^k $
Passiamo al secondo fattore:
$ (1 + frac(1)(n^3) )^n $
In questo caso risulta più difficile applicare lo stesso procedimento, in quanto gli esponenti di $n$ sono diversi.
Possiamo, però, cercare di ricostruire l’espressione che ci serve per poter applicare il limite notevole; in particolare, possiamo moltiplicare e dividere l’esponente $n$ per $n^3$:
$ (1 + frac(1)(n^3) )^n = (1 + frac(1)(n^3) )^(n * n^3 * 1/n^3) $
Per le proprietà delle potenze, inoltre, otteniamo la seguente forma equivalente:
$ [ (1 + frac(1)(n^3) )^(n^3) ]^(n * 1/n^3) = [ (1 + frac(1)(n^3) )^(n^3) ]^(1/n^2) $
A questo punto, il termine dentro parentesi quadre può essere trattato come limite notevole, mentre l’esponente $ 1/n^2 $ tende a $0$ per $ n to oo$:

Quindi, passando al limite abbiamo:
$ lim_(n to +oo) [ (1 + frac(1)(n^3) )^(n^3) ]^(1/n^2) = e^0 = 1 $
Passiamo, infine, al terzo ed ultimo fattore:
$ (1 + frac(1)(n^3) )^1 $
Per questo fattore non solo necessari ulteriori passaggi, in quanto siamo in grado di determinare facilmente il suo valore al limite:
$ lim_(n to +oo) (1 + frac(1)(n^3) )^1 = 1 $
Riorganizzando il limite iniziale, abbiamo che:
$ lim_(n to +oo) ( 1 + frac(1)(n^3) )^(πn^3 + n + 1) = $
$ lim_(n to +oo) [( 1 + frac(1)(n^3) )^(πn^3) * ( 1 + frac(1)(n^3) )^n * ( 1 + frac(1)(n^3) )^1] = $
$ lim_(n to +oo) ( 1 + frac(1)(n^3) )^(πn^3) * lim_(n to +oo)( 1 + frac(1)(n^3) )^n * lim_(n to +oo)( 1 + frac(1)(n^3) )^1 = $
$ e^π * 1 * 1 = e^π $
Potrebbe interessarti anche
- Appunti sui Limiti di successione
- Appunti sui Limiti