Alla fine degli anni 70 una azienda decise di valutare l’opportunità del passaggio da una struttura organizzativa funzionale ad una struttura divisionale. Come è noto la struttura funzionale accentra le principali funzioni aziendali, nel caso: Direzione Operativa, Direzione Tecnica, Approvvigionamenti, Commerciale. Continua a leggere “Ristrutturazione”
Autore: stan
Affidabilità
L’affidabilità (reliability) di un sistema, un’apparecchiatura, un circuito, misura la sua probabilità di funzionare correttamente per un tempo predeterminato (tempo di missione).
Naturalmente qualunque sistema dal più semplice, una lampadina, al più complesso, un satellite, è composto da più parti che tutte debbono contribuire per il funzionamento complessivo dell’intero sistema. Continua a leggere “Affidabilità”
Slitta
Luca e Piero sono grandi appassionati della montagna. Abili sciatori, sci-alpinisti, scalatori.
A inizio dell’inverno hanno convinto un amico a prestare loro una baita sulle Dolomiti. Non ci sono mai stati, ma dalla narrazione del proprietario capiscono che il luogo è incantevole: campi da sci, rocce, crepacci tra vette imponenti. Continua a leggere “Slitta”
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x=0$ fino al secondo ordine: $f(x)=e^x log(1+x) cos(x)$
Per risolvere l’esercizio, possiamo avvalerci degli sviluppi fondamentali delle funzioni esponenziale, coseno e logaritmo; ricordiamo che le funzioni hanno i seguenti sviluppi:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + … + frac(z^n)(n!) + o(z^n) $
$ log(1+z) = z – frac(z^2)(2) + frac(z^3)(3) + … + (-1)^(n+1) frac(z^n)(n) + o(z^n) $
$ cos(z) = 1 – frac(z^2)(2) + frac(z^4)(24) – … + frac((-1)^n z^(2n))((2n)!) + o(z^(2n)) $
Poiché è richiesto uno sviluppo al secondo ordine della funzione $f(x)$, e dato che essa è data dal prodotto delle funzioni esponenziale, logaritmo e coseno, sarà sufficiente sviluppare tali funzioni nel modo seguente: la funzione esponenziale può essere sviluppata al primo ordine:
$ e^z = 1 + x + o(x) $
mentre le funzioni coseno e logaritmo entrambe al secondo ordine:
$ log(1+x) = x – frac(x^2)(2) + o(x^2) $
$ cos(z) = 1 – frac(x^2)(2) + o(x^2) $
In questo modo otterremo uno sviluppo della funzione di partenza al secondo ordine; procediamo con i prodotti:
$ f(x) = e^x log(1+x) cos(x) = (1 + x + o(x)) * (x – frac(x^2)(2) + o(x^2)) * (1 – frac(x^2)(2) + o(x^2)) $
Per semplicità svolgiamo inizialmente il prodotto tra i primi due fattori:
$ f(x) = ( x + x^2 + o(x^2) – frac(x^2)(2) – frac(x^3)(2) + o(x^3) ) * (1 – frac(x^2)(2) + o(x^2)) $
Come sappiamo, gli infinitesimi di ordine maggiore vengono inglobati da quelli di ordine minore, quindi in questo caso le potenze di 3 verranno inglobate all’interno di $o(x^2)$:
$ f(x) = ( x + frac(x^2)(2) + o(x^2) ) * (1 – frac(x^2)(2) + o(x^2)) $
Procediamo quindi con il secondo prodotto:
$ f(x) = x – frac(x^3)(2) + o(x^3) + frac(x^2)(2) – frac(x^4)(4) + o(x^4) + o(x^2) $
Applicando lo stesso ragionamento visto in precedenza, possiamo ottenere il risultato finale:
$ f(x) = x + frac(x^2)(2) + o(x^2) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Sia data la seguente seguente funzione: $f(x)=root(3)(1+4x) + root(4)(1- 3x) – 2$ calcolare lo sviluppo in serie di Taylor della funzione al terzo ordine
L’esercizio chiede di calcolare lo sviluppo di Taylor al terzo ordine della funzione; in questo caso, non essendoci funzioni di sviluppo noto, dobbiamo procedere applicando la definizione, ovvero la formula del polinomio di Taylor:
$ T_n (f , x) = f(x_0) + f’(x_0) (x – x_0) + frac(f’’(x_0))(2!) (x – x_0)^2 + … + frac(f^n(x_0))(n!) (x – x_0)^n $
In questo caso, dovendoci fermare al terzo ordine, dobbiamo calcolare le derivate della funzione fino a quella di terzo ordine.
Per semplicità, chiamiamo con $g(x)$ e $h(x)$ le funzioni:
$ g(x) = root(3)(1+4x) $
$ h(x) = root(4)(1- 3x) $
e calcoliamo le loro derivate separatamente.
Cominciamo con $g(x)$.
Il termine di ordine zero coincide con la funzione stessa; la funzione in zero vale 1:
$ g(0) = 1$
Passiamo alla derivata prima:
$ g’(x) = \frac{1}{3} (1+4x)^{ – \frac{2}{3}} * 4 = \frac{4}{3 root(3)((1+4x)^2)} $
Calcoliamo il valori assunti da tale derivata nel punto $x=0$:
$ g’(0) = 4/3 $
Calcoliamo la derivata seconda:
$ g’’(x) = \frac{4}{3} * (- \frac{2}{3}) * (1 + 4x)^{-\frac{5}{3}} * 4 = – \frac{32}{9 root(3)((1+4x)^5) } $
I valori assunti dalla derivata nel punto $x=0$ sono:
$ g’’(0) = – (32)/9 $
Passiamo, infine alla derivata terza:
$ g’’’(x) = \frac{32}{9} * (- \frac{5}{3}) * (1 + 4x)^{-\frac{8}{3}} * 4 = – \frac{640}{27 root(3)((1+4x)^8) } $
Anche in questo caso, calcoliamo il valore assunto dalla derivata in zero:
$ g’’’(0) = (640)/(27) $
Possiamo ora scrivere lo sviluppo in serie di Taylor al terzo ordine della funzione $g(x)$:
$ g(x) = 1 + 4/3 x – (32)/9 frac(x^2)(2) + (640)/(27) frac(x^3)(6) + o(x^3) $
Moltiplicando e semplificando si ha:
$ g(x) = 1 + 4/3 x – (16)/9 x^2 + (320)/(81) x^3 + o(x^3) $
Applichiamo lo stesso procedimento alla funzione $h(x)$, calcolando le sue derivate fino a quella di ordine terzo, e per ciascuna di essa il valore assunto in $x=0$:
Il termine di ordine zero è la funzione stessa; la funzione in zero vale 1:
$ h(0) = 1$
Passiamo alla derivata prima:
$ h’(x) = \frac{1}{4} (1-3x)^{ – \frac{3}{4}} * (-3) = – \frac{3}{4 root(4)((1-3x)^3)} $
Calcoliamo il valori assunti da tale derivata nel punto $x=0$:
$ h’(0) = -3/4 $
Calcoliamo la derivata seconda:
$ h’’(x) = – \frac{3}{4} * (- \frac{3}{4}) (1-3x)^{ – \frac{7}{4}} * (-3) = – \frac{27}{16 root(4)((1-3x)^7)} $
I valori assunti dalla derivata nel punto $x=0$ sono:
$ h’’(0) = – (27)/(16) $
Passiamo, infine alla derivata terza:
$ h’’’(x) = -\frac{27}{16} * (- \frac{7}{4}) * (1 – 3x)^{-\frac{11}{4}} * (-3) = – \frac{567}{64 root(3)((1-3x)^{11})} $
Anche in questo caso, calcoliamo il valore assunto dalla derivata in zero:
$ g’’’(0) = -(567)/(64) $
Possiamo quindi scrivere lo sviluppo in serie di Taylor al terzo ordine della funzione $h(x)$:
$ h(x) = 1 – 3/4 x – (27)/(16) frac(x^2)(2) – (567)/(64) frac(x^3)(6) + o(x^3) $
Moltiplicando e semplificando si ha:
$ h(x) = 1 – 3/4 x – (27)/(32) x^2 – (189)/(128) x^3 + o(x^3) $
A questo punto, possiamo determinare lo sviluppo in serie di Taylor della funzione $f(x)$; sostituiamo alle funzioni $g(x)$ e $h(x)$ i loro sviluppi appena calcolati:
$ f(x) = root(3)(1+4x) + root(4)(1- 3x) – 2 = $
$ 1 + 4/3 x – (16)/9 x^2 + (320)/(81) x^3 + o(x^3) + 1 – 3/4 x – (27)/(32) x^2 – (189)/(128) x^3 + o(x^3) = $
$ 7/(12) x – frac(755)(288) x^2 + ((320)/(81) – (189)/(128)) x^3 + o(x^3) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x_0=0$ fino al quinto ordine: $f(x)=e^(x^2 log(1+x(x+1)))+x sin(x)$
La funzione si presenta in una forma per la quale è possibile applicare lo sviluppo noto di alcune funzioni; in particolare, in questo caso gli sviluppi che verranno utilizzati sono quelli delle funzioni esponenziale, logaritmo e seno, che ricordiamo essere i seguenti:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + … + frac(z^n)(n!) + o(z^n) $
$ log(1+z) = z- frac(z^2)(2) + frac(z^3)(3) + … + (-1)^(n+1) frac(z^n)(n) + o(z^n) $
$ sin(x) = x – frac(x^3)(6) + frac(x^5)(120) – … + frac((-1)^n x^(2n+1))((2n+1)!) + o(x^(2n+1)) $
Possiamo procedere concentrandoci inizialmente sulla prima parte della funzione, ovvero il termine $e^( x^2 log( 1 + x(x+1) ) )$ e sviluppando tale termine al quinto ordine di infinitesimo.
Per farlo, notiamo che l’argomento dell’esponenziale è dato dal prodotto di una funzione logaritmica e di una potenza di x ($x^2$).
Per ottenere un quinto grado, quindi, sarà necessario sviluppare $log( 1 + x(x+1) ) $ al terzo ordine.
Procediamo, quindi, sviluppando la funzione $log(1+z)$ al terzo ordine:
$ log(1+z) = z- frac(z^2)(2) + frac(z^3)(3) + o(z^3) $
Ora, possiamo apportare la seguente sostituzione: $ z = x(x+1) = x^2 + x $; l’uguaglianza $ o(z) = o( x + x^2)$ è valida, in quanto il comportamento delle funzioni $x$ e $ x^2 + 2$ è pressoché uguale quando x tende a zero.
Procediamo, quindi, con la sostituzione:
$ log(1+ x(x+1)) = x^2 + x – frac((x^2 + x)^2)(2) + frac((x^2 + x)^3)(3) + o((x^2 + x)^3) $
Svolgiamo i calcoli:
$ log(1+ x(x+1)) = x^2 + x -1/2 x^4 – 1/2 x^2 – x^3 + 1/3 x^6 + 1/3 x^3 + x^5 + x^4 + o( x^3) $
Possiamo tralasciare i termini con esponenti maggiori di 3, in quanto essi vengono considerati all’interno di $ o(x^3)$:
$ log(1+ x(x+1)) = x^2 + x – 1/2 x^2 – x^3 + 1/3 x^3 + o( x^3) = x + 1/2 x^2 – 2/3 x^3 + o( x^3) $
Nella funzione di partenza, tale logaritmo è moltiplicato per il fattore $x^2$:
$ x^2 * log(1+ x(x+1)) = x^2 [ x + 1/2 x^2 – 2/3 x^3 + o( x^3)] = $
$ x^3 + 1/2 x^4 – 2/3 x^5 + o( x^5) $
Tale espressione costituisce l’esponente di un’esponenziale; per poter determinare lo sviluppo complessivo, dobbiamo inizialmente calcolare lo sviluppo della funzione esponenziale; sarà sufficiente fermarsi al secondo ordine, ottenendo un sesto ordine complessivo:
$ e^z = 1 + z + frac(z^2)(2) + o(z^2) $
Sostituiamo a $z$ l’espressione $ x^3 + 1/2 x^4 – 2/3 x^5 + o( x^5) $ :
$ e^(x^2 * log(1+ x(x+1))) = 1 + [x^3 + 1/2 x^4 – 2/3 x^5 + o( x^5)] + frac((x^3 + 1/2 x^4 – 2/3 x^5
+ o( x^5))^2)(2) + o((x^3 + 1/2 x^4 – 2/3 x^5 + o( x^5))^2) $
Come prima, nello svolgimento dei calcoli, possiamo tralasciare i termini che presentano esponenti maggiori di 5, che verranno ravvolti all’interno di $o(x^5)$:
$ e^(x^2 * log(1+ x(x+1))) = 1 + x^3 + 1/2 x^4 – 2/3 x^5 + 1/2 x^6 + o(x^5) $
Possiamo quindi procedere con lo sviluppo della seconda parte della funzione, ovvero con lo sviluppo dell’espressione $x sin(x) $; in questo caso, dobbiamo sviluppare solo la funzione seno, e lo sviluppo dovrà essere di quarto ordine (moltiplicato per x ci consentirà di ottenere un quinto ordine complessivo).
Lo sviluppo della funzione seno è il seguente:
$ sin(x) = x – frac(x^3)(6) + o(x^4) $
Moltiplichiamo tale espressione per x:
$ x * sin(x) = x * [x – frac(x^3)(6) + o(x^4)] = x^2 – frac(x^4)(6) + o(x^5) $
Possiamo infine determinare lo sviluppo complessivo della funzione di partenza:
$ f(x) = e^( x^2 log( 1 + x(x+1) ) ) + x sin(x) = $
$1 + x^3 + 1/2 x^4 – 2/3 x^5 + 1/2 x^6 + o(x^5) + x^2 – frac(x^4)(6) + o(x^5) = $
$ 1 + x^2 + x^3 + 1/3 x^4 – 2/3 x^5 + o(x^5) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x_0=1$ fino al quarto ordine: $f(x)=x^(x – 1)$
Per la risoluzione di questo esercizio possiamo usare due strade; poiché non possiamo usare gli sviluppi fondamentali (almeno non direttamente), possiamo utilizzare il metodo classico, ovvero applicare la formula dello sviluppo di Taylor, calcolando le derivate (fino alla quarta) della funzione di partenza, e il valore che esse assumono nel punto $x_0=1$.
Oppure possiamo ragionare diversamente, trasformando la nostra funzione in modo da poter applicare gli sviluppi fondamentali.
Notiamo che il punto richiesto nello sviluppo della funzione, ovvero $x_0=1$, può essere scritto che nel seguente modo: $x_0 – 1 = 0$; questo ci suggerisce che, applicando la sostituzione $ x_0 – 1 = t$, ci ritroviamo nel caso classico, perché in questo modo lo sviluppo sarà centrato nel punto $ t = 0$.
Procediamo, quindi, sostituendo nella funzione di partenza $ x-1 = t to x = t + 1$:
$ f(x) = f(t+1) = (t+1)^(t+1 – 1) = (t+1)^t $
Applicando le proprietà che lega potenze e funzione esponenziale, è possibile scrivere la nostra funzione nel seguente modo:
$ f(t+1) = e^(t log(t+1)) $
Notiamo, quindi, che ci siamo ricondotti in un caso classico, che possiamo risolvere facilmente con gli sviluppi fondamentali; in questo caso utilizzeremo lo sviluppo della funzione esponenziale, e della funzione logaritmica, che ricordiamo essere i seguenti:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + … + frac(z^n)(n!) + o(z^n) $
$ log(1+z) = z- frac(z^2)(2) + frac(z^3)(3) + … + (-1)^(n+1) frac(z^n)(n) + o(z^n) $
Per ottenere uno sviluppo al quarto ordine della funzione di partenza, possiamo sviluppare la funzione logaritmo al terzo ordine, ottenendo il seguente sviluppo:
$ log(1+t) = t – frac(t^2)(2) + frac(t^3)(3) + o(t^3) $
Moltiplicando per $t$ abbiamo la seguente espressione, che rappresenta l’esponente dell’esponenziale:
$ t log(1+t) = t^2 – frac(t^3)(2) + frac(t^4)(3) + o(t^4) $
Procediamo ora sviluppando la funzione esponenziale al quarto ordine:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + frac(z^4)(4!) + o(z^4) $
A questo punto dobbiamo sostituire l’espressione precedentemente trovata per l’esponente, alla $z$ che compare nello sviluppo dell’esponenziale; la sostituzione è quindi la seguente:
$ z = t^2 – frac(t^3)(2) + frac(t^4)(3) + o(t^4) $
Per semplicità, possiamo procedere calcolando singolarmente le potenze di $z$; per $z^2$
abbiamo:
$ z^2 = (t^2 – frac(t^3)(2) + frac(t^4)(3) + o(t^4))^2 $
Nell’esecuzione dei calcoli, possiamo tralasciare le potenze con esponente maggiore di 4, in quanto, per le proprietà dell’o-piccolo, esse verranno inglobate all’interno di $o(t^4) $:
$ z^2 = t^4 + o(t^4) $
Nel caso di $z^3$ e $z^4$ si ottengono tutte potenze di grado maggiore di 4.
Procediamo quindi sostituendo i valori trovati precedentemente nello sviluppo di $e^z$:
$ e^(t log(t+1)) = 1 + t^2 – frac(t^3)(2) + frac(t^4)(3) + o(t^4) + frac(t^4)(2) + o(z^4) = $
$ 1 + t^2 – frac(t^3)(2) + 5/6 t^4 + o(z^4) $
A questo punto, dobbiamo ricondurre l’espressione trovata in funzione di x, come era nella funzione di partenza; per farlo, ricordiamo la sostituzione effettuata, ovvero $ x = t+1$, q applichiamo la sostituzione inversa, cioè $ t = x – 1$; otteniamo il seguente sviluppo:
$ e^((x-1) log(x)) = 1 + (x – 1)^2 – 1/2 (x – 1)^3 + 5/6 (x – 1)^4 + o((x – 1)^4) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x_0=0$ fino al terzo ordine: $f(x)=e^(x + x^2)$
Per la risoluzione dell’esercizio possiamo avvalerci degli sviluppi fondamentali delle funzione esponenziale, in quanto lo sviluppo richiesto della funzione di partenza è centrato nel punto $x_0=0$.
Ricordiamo, quindi, che lo sviluppo fondamentale è il seguente:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + … + frac(z^n)(n!) + o(z^n) $
Per poter ottenere uno sviluppo al terzo ordine della funzione di partenza è necessario sviluppare la funzione esponenziale al terzo ordine:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + o(z^3) $
Possiamo quindi effettuare la seguente sostituzione: $ z = x + x^2$; questo è possibile in quanto il comportamento di $x$ e quello di $ x + x^2$ sono pressoché uguali quando x tende a zero, e quindi vale anche la seguente uguaglianza tra o-piccoli: $ o(x + x^2) = o(z) $.
Possiamo quindi procedere con la sostituzione:
$ e^x = 1 + x + x^2 + frac((x + x^2)^2)(2) + frac((x + x^2)^3)(6) + o((x + x^2)^3) $
Svolgiamo i calcoli:
$ e^x = 1 + x + x^2 + frac(x^2 + x^4 + 2x^3)(2) + frac(x^3 + x^6 + 3x^4 + 3x^5)(6) + o(x^3) = $
$ 1 + x + x^2 + 1/2 x^2 + 1/2 x^4 + x^3 + 1/6 x^3 + 1/6 x^6 + 1/2 x^4 + 1/2 x^5 + o(x^3) $
Possiamo tralasciare i termini che presentano esponenti maggiori di tre, in quanto, per le proprietà dell’o-piccolo, essi vengono inglobati all’interno di $ o(x^3)$; quindi abbiamo:
$ e^x = 1 + x + 3/2 x^2 + 7/6 x^3 + o(x^3)$
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x_0=0$ fino al quarto ordine: $f(x)=x*log(sin(x)+cos(x))$
Per la risoluzione dell’esercizio possiamo avvalerci degli sviluppi fondamentali delle funzioni logaritmo, seno e coseno, in quanto lo sviluppo richiesto della funzione di partenza è centrato nel punto $x_0=0$.
Ricordiamo, quindi, che gli sviluppi fondamentali sono i seguenti:
per la funzione logaritmica si ha:
$ log(1+z) = z- frac(z^2)(2) + frac(z^3)(3) + … + (-1)^(n+1) frac(z^n)(n) + o(z^n) $
per la funzione seno:
$ sin(x) = x – frac(x^3)(6) + frac(x^5)(120) – … + frac((-1)^n x^(2n+1))((2n+1)!) + o(x^(2n+1)) $
e infine per la funzione coseno:
$ cos(x) = 1 – frac(x^2)(2) + frac(x^4)(24) – … + frac((-1)^n x^(2n))((2n)!) + o(x^(2n)) $
Possiamo quindi procedere allo svolgimento; per comodità, possiamo considerare inizialmente solo l’espressione che costituisce il secondo fattore della funzione, e sviluppare essa al terzo ordine. Essendo poi moltiplicata per x, ci fornirà un quanto ordine della funzione di partenza.
Cominciamo quindi sviluppando le funzioni seno e coseno al quarto ordine:
$ sin(x) = x – frac(x^3)(6) + o(x^4) $
$ cos(x) = 1 – frac(x^2)(2) + frac(x^4)(24) + o(x^4) $
Ora, possiamo procedere determinando lo sviluppo della funzione logaritmo al quarto ordine:
$ log(1+z) = z- frac(z^2)(2) + frac(z^3)(3) – frac(z^4)(4) + o(z^4) $
Tornando all’espressione presente, abbiamo che l’argomento del logaritmo è dato da:
$ sin(x) + cos(x) = x – frac(x^3)(6) + o(x^4) + 1 – frac(x^2)(2) + frac(x^4)(24) + o(x^4) = $
$ 1 + x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) + o(x^4) $
Quindi, la sostituzione che dobbiamo effettuare è la seguente:
$ z = x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) + o(x^4) $
Per semplificare i calcoli, possiamo tralasciare tutte le potenze di grado maggiore di quattro, in quanto esse vengono incluse all’interno di $ o(x^4)$; procediamo calcolando separatamente le varie potenze di $z$:
$ z^2 = (x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) + o(x^4))^2 = x^2 – x^3 – frac(1)(12) x^4 + o(x^4) $
$ z^3 = (x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) + o(x^4))^3 = x^3 – frac(3)(2) x^4 + o(x^4) $
$ z^4 = (x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) + o(x^4))^4 = x^4 + o(x^4) $
Possiamo ora sostituire le espressioni trovate nello sviluppo del logaritmo:
$ log(1+z) = z- frac(z^2)(2) + frac(z^3)(3) – frac(z^4)(4) + o(z^4) = $
$ x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) + o(x^4) – 1/2 (x^2 – x^3 – frac(1)(12) x^4 + o(x^4)) + 1/3 (x^3 – frac(3)(2) x^4 + o(x^4)) – 1/4 (x^4 + o(x^4)) $
Svolgiamo i calcoli:
$ log(1+z) = x – frac(x^2)(2) – frac(x^3)(6) + frac(x^4)(24) – 1/2 x^2 + 1/2 x^3 + frac(1)(24) x^4 + 1/3 x^3 – frac(1)(2) x^4 – 1/4 x^4 + o(x^4)) = $
$ x – x^2 + frac(2)(3) x^3 – 2/3 x^4 + o(x^4)) $
Moltiplichiamo ora tutto per x, ottenendo così lo sviluppo finale:
$ x log(1+z) = x^2 – x^3 + frac(2)(3) x^4 + o(x^4) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x_0=0$ fino al settimo ordine: $f(x)=x*e^(sin(x^2))$
Per la risoluzione dell’esercizio possiamo avvalerci degli sviluppi fondamentali delle funzioni esponenziale e seno, in quanto lo sviluppo richiesto della funzione di partenza è centrato nel punto $x_0=0$.
Ricordiamo lo sviluppo fondamentale della funzione seno:
$ sin(z) = z – frac(z^3)(6) + frac(z^5)(120) – … + frac((-1)^n z^(2n+1))((2n+1)!) + o(z^(2n+1)) $
e della funzione esponenziale:
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + … + frac(z^n)(n!) + o(z^n) $
Possiamo inizialmente concentrarci sull’espressione $e^(sin(x^2)) $, e svilupparla al sesto ordine; in questo modo, in quanto moltiplicata per $x$ nella funzione di partenza, otterremo un settimo ordine totale.
Possiamo quindi cominciare provando a sviluppare la funzione seno al terso ordine:
$ sin(z) = z – frac(z^3)(6) + o(z^3) $
Poiché nella nostra funzione l’argomento del seno è $x^2$, è necessario apportare la sostituzione $ z=x^2$. Possiamo effettuare tale sostituzione in quanto, al tendere di x a zero, si ha che $ x = x^2$, e quindi possiamo affermare che $ o(z) = o(x)$.
Abbiamo quindi:
$ sin(x^2) = x^2 – frac((x^2)^3)(6) + o((x^2)^3) = x^2 – frac( x^6 )(6) + o( x^6 ) $
A questo punto, sviluppiamo la funzione esponenziale al terzo ordine (questo è necessario, perché altrimenti se ci fermassimo al primo o al secondo ordine, non sarebbe possibile raggiungere un sesto ordine complessivo, a causa delle proprietà algebriche dell’o-piccolo):
$ e^z = 1 + z + frac(z^2)(2) + frac(z^3)(6) + o(z^3) $
In questo caso, quindi, la sostituzione da effettuare è la seguente, valida per il ragionamento effettuato in precedenza: $ z = x^2 – frac( x^6 )(6) + o( x^6 ) $
Procediamo con i calcoli:
$ e^(sin(x^2)) = 1 + (x^2 – frac( x^6 )(6) + o( x^6 )) + frac((x^2 – frac( x^6 )(6) + o( x^6 ))^2)(2) + frac((x^2 – frac( x^6 )(6) + o( x^6 ))^3)(6) + o((x^2 – frac( x^6 )(6) + o( x^6 ))^3) $
Semplifichiamo l’espressione:
$ e^(sin(x^2)) = 1 + x^2 – frac( x^6 )(6) + o( x^6 ) + 1/2 x^4 + frac(x^(12))(72) – frac(x^8)(6) + 1/6 x^6 – frac(x^(10))(12) + frac(x^(14))(12) – frac(x^(18))(6^4) + o( x^6 ) $
Possiamo tralasciare tutti i termini che presentano potenze maggiori di 6, in quanto essi, per le proprietà dell’o-piccolo, vengono considerate all’interno di $o( x^6 ) $; l’espressione diventa quindi:
$ e^(sin(x^2)) = 1 + x^2 – frac( x^6 )(6) + 1/2 x^4 + 1/6 x^6 + o( x^6 ) = $
$ 1 + x^2 + 1/2 x^4 + o( x^6 ) $
Possiamo quindi procedere determinando lo sviluppo al settimo ordine della funzione di partenza:
$ f(x) = x * e^(sin(x^2)) = x * (1 + x^2 + 1/2 x^4 + o( x^6 )) = x + x^3 + 1/2 x^5 + o( x^7 ) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x_0=0$ fino al sesto ordine: $f(x)=6 sin^2(x)+log(1 + x^2)$
Dato che l’esercizio richiede lo sviluppo in serie di Taylor della funzione nel punto $x_0=0$, possiamo avvalerci degli sviluppi fondamentali della funzione seno e della funzione logaritmo; ricordiamo che gli sviluppi fondamentali sono i seguenti:
$ sin(z) = z – frac(z^3)(6) + frac(z^5)(120) – … + frac((-1)^n z^(2n+1))((2n+1)!) + o(z^(2n+1)) $
$ log(1+z) = z – frac(z^2)(2) + frac(z^3)(3) + … + (-1)^(n+1) frac(z^n)(n) + o(z^n) $
Cominciamo dallo sviluppo della prima funzione; poiché la funzione seno è elevata al quadrato, per ottenere uno sviluppo al sesto ordine della funzione di partenza, occorre sviluppare $sin(z)$ al quinto ordine, ottenendo il seguente sviluppo:
$ sin(z) = z – frac(z^3)(6) + frac(z^5)(120) + o(z^5) $
In questo caso, la sostituzione sarà semplicemente $ z = x$; quindi avremo:
$ sin(x) = x – frac(x^3)(6) + frac(x^5)(120) + o(x^5) $
All’interno della nostra funzione, tale espressione è elevata al quadrato e moltiplicata per un fattore 6:
$ 6 (sin(x))^2 = 6 (x – frac(x^3)(6) + frac(x^5)(120) + o(x^5))^2 $
Procediamo quindi al calcolo del quadrato, ricordando le proprietà algebriche dell’o-piccolo:
$ 6 (sin(x))^2 = 6 (x^2 + frac(x^6)(36) + frac(x^10)(120^2) – frac(x^4)(3) + frac(x^6)(60) – frac(x^8) (360) + o(x^6)) $
Come sappiamo, possiamo eliminare tutte le potenze di grado maggiore a 6, in quanto esse vengono inglobate all’interno di $o(x^6)$; quindi abbiamo:
$ 6 (sin(x))^2 = 6 (x^2 + frac(x^6)(36) – frac(x^4)(3) + frac(x^6)(60) + o(x^6)) = $
$ 6 x^2 + frac(x^6)(6) – 2x^4 + frac(x^6)(10) + o(x^6) = 6 x^2 – 2x^4 + frac(4 x^6)(15) + o(x^6) $
Procediamo con lo stesso ragionamento determinando lo sviluppo del logaritmo; questa volta, però, considerando il grado dell’argomento, possiamo fermare lo sviluppo di $log(z)$ al terso ordine:
$ log(1+z) = z – frac(z^2)(2) + frac(z^3)(3) + o(z^3) $
Effettuiamo ora la sostituzione $ z = x^2$, tenendo presente che per $x to 0$ si ha che $ x = x^2$, e quindi possiamo affermare che $ o(z) = o(x^2) $:
$ log(1+ x^2) = x^2 – frac((x^2)^2)(2) + frac((x^2)^3)(3) + o((x^2)^3) = $
$ x^2 – frac(x^4)(2) + frac(x^6)(3) + o(x^6) $
Possiamo quindi determinare lo sviluppo della funzione di partenza:
$ f(x) = 6 sin^2(x) + log(1 + x^2) = $
$6 x^2 – 2x^4 + frac(4 x^6)(15) + o(x^6) + x^2 – frac(x^4)(2) + frac(x^6)(3) + o(x^6) = $
$ 7 x^2 – frac(5 x^4)(2) + frac(3 x^6)(5) + o(x^6) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x=0$ fino all’ottavo ordine: $ f(x)=sin(x^2 + x^3)$
Per la risoluzione dell’esercizio ricordiamo lo sviluppo fondamentale della funzione seno nel punto $x=0$:
$ sin(z) = z – frac(z^3)(6) + frac(z^5)(120) – … + frac((-1)^n z^(2n+1))((2n+1)!) + o(z^(2n+1)) $
In questo caso, è possibile effettuare la sostituzione $ z = x^2 + x^3$, in quanto per x tendente a zero, si ha che $ x = x^2 + x^3 $, e quindi anche che $ o(z) = o(x^2 + x^3) $.
Essendo l’argomento della funzione seno di terzo grado, per poter raggiungere uno sviluppo all’ottavo ordine, sarà sufficiente sviluppare la funzione $sin(z)$ fino al terzo ordine:
$ sin(z) = z – frac(z^3)(6) + o(z^3) $
Effettuiamo ora la sostituzione:
$ sin((x^2 + x^3)) = (x^2 + x^3) – frac((x^2 + x^3)^3)(6) + o((x^2 + x^3)^3) $
Svolgiamo i calcoli:
$ sin((x^2 + x^3)) = x^2 + x^3 – frac( (x^2)^3 + (x^3)^3 + 3 (x^2)^2 * x^3 + 3 x^2 * (x^3)^2 )(6) + o((x^2 + x^3)^4) $
$ sin((x^2 + x^3)) = x^2 + x^3 – frac( x^6 + x^9 + 3 x^7 + 3 x^8 )(6) + o((x^2 + x^3)^4) $
Senza svolgere la quarta potenza all’interno dell’o-piccolo, possiamo facilmente vedere che la potenza di grado minore che comparirà come argomento sarà proprio quella di quarto grado; quindi possiamo direttamente scrivere $ o((x^2 + x^3)^4) = o(x^8) $:
$ sin((x^2 + x^3)) = x^2 + x^3 – 1/6 x^6 – 1/6 x^9 – 1/2 x^7 – 1/2 x^8 + o(x^8) $
Di conseguenza, possiamo eliminare tutti i termini che presentano potenze di x maggiori di 8, in quanto essi verranno “inglobati” all’interno dell’o-piccolo di ottavo ordine:
$ sin((x^2 + x^3)) = x^2 + x^3 – 1/6 x^6 – 1/2 x^7 – 1/2 x^8 + o(x^8) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x=1$ fino al quarto ordine: $f(x)=x^(log(x))$
Per lo svolgimento di questo esercizio, non possiamo avvalerci degli sviluppi di Taylor fondamentali, in quanto la funzione di partenza è una funzione composta, e lo sviluppo richiesto è centrato in un punto diverso da zero.
Dobbiamo procedere, quindi, calcolando le derivate di ordine primo, secondo, terzo e quarto della funzione, e calcolare il valore da esse assunto nel punto $ x = 1$.
In questo caso, quindi, occorre applicare fedelmente la formula del polinomio di Taylor:
$ T_n (f , x) = f(x_0) + f’(x_0) (x – x_0) + frac(f’’(x_0))(2!) (x – x_0)^2 + … + frac(f^n(x_0))(n!) (x -x_0)^n $
Calcoliamo quindi il valore della funzione in 1, ovvero $ f(x_0)$:
$ f(1) = 1^(log(1)) = 1^0 = 1 $
Procediamo calcolando la derivata prima della funzione; semplifichiamo i calcoli trasformando la funzione nel seguente modo:
$ f(x) = x^(log(x)) = e^(log(x)*log(x)) = e^(log^2(x)) $
Quindi abbiamo:
$ f’(x) = frac(d)(dx) e^(log^2(x)) = e^(log^2(x)) * frac(2 log(x) )(x)$
Calcoliamo il valore che la derivata prima assume in $ x = 1$:
$ f’(1) = e^(log^2(1)) * frac(2 log(1) )(1) = 0 $
Procediamo ora con la derivata seconda:
$ f’’(x) = frac(d)(dx) e^(log^2(x)) * frac(2 log(x) )(x) = [e^(log^2(x)) * frac(2 log(x) )(x) * frac(2 log(x) ) (x) ] + [e^(log^2(x)) * frac(2(1-log(x)))(x^2)] $
Svolgiamo tutti i calcoli e semplifichiamo:
$ f’’(x) = [ 4 e^(log^2(x)) * frac(log^2(x) )(x^2) ] + [2e^(log^2(x)) * frac(1-log(x))(x^2)] $
Possiamo effettuare un raccoglimento totale:
$ f’’(x) = 2e^(log^2(x)) [ 2 frac(log^2(x) )(x^2) + frac(1-log(x))(x^2)] = 2 frac(e^(log^2(x)))(x^2) [ 2 log^2(x) – log(x) +1] $
Calcoliamo il valore della derivata seconda nel punto $ x = 1$:
$ f’’(1) = 2 frac(e^(log^2(1)))(1^2) [ 2 log^2(1) – log(1) +1] = 2 $
Proseguiamo con la derivata terza della funzione:
$ f’’’(x) = frac(d)(dx) {2 frac(e^(log^2(x)))(x^2) [ 2 log^2(x) – log(x) +1]} = $
$ [4 e^(log^2(x)) * frac(log(x) – 1)(x^3) ][ 2 log^2(x) – log(x) +1] + 2 frac(e^(log^2(x)))(x^2) * [4 frac(log(x))(x) – 1/x ] $
Svolgiamo i calcoli e semplifichiamo; per agevolare i calcoli effettuiamo un raccoglimento totale:
$ f’’’(x) = e^(log^2(x)) {[4 * frac(log(x) – 1)(x^3) ][ 2 log^2(x) – log(x) +1] + 2 frac(1)(x^2) * [4 frac(log(x))(x) – 1/x ]} = $
$ e^(log^2(x)) {[4 * frac(log(x) – 1)(x^3) ][ 2 log^2(x) – log(x) +1] + 2 frac(1)(x^3) * [4 log(x) – 1 ]} = $
$ frac(e^(log^2(x)))(x^3) {[4 (log(x) – 1) ][ 2 log^2(x) – log(x) +1] + 2 [4 log(x) – 1 ]} = $
$ frac(e^(log^2(x)))(x^3) { (4log(x) – 4) (2 log^2(x) – log(x) +1) + 8 log(x) – 2 } = $
$ 2 frac(e^(log^2(x)))(x^3) { (2log(x) – 2) (2 log^2(x) – log(x) +1) + 4 log(x) – 1 } = $
$ 2 frac(e^(log^2(x)))(x^3) ( 4 log^3(x) – 6 log^2(x) + 8 log(x) – 3) $
Calcoliamo il valore della derivata terza nel punto $ x = 1$:
$ f’’’(1) = 2 frac(e^(log^2(1)))(1^3) ( 4 log^3(1) – 6 log^2(1) + 8 log(1) – 3) = – 6 $
Procediamo con l’ultima derivata, quella di ordine quarto:
$ f^(4)(x) = frac(d)(dx) [2 frac(e^(log^2(x)))(x^3) ( 4 log^3(x) – 6 log^2(x) + 8 log(x) – 3)] = $
$ [2 frac(e^(log^2(x)))(x^4) * (2log(x) – 3) ] * ( 4 log^3(x) – 6 log^2(x) + 8 log(x) – 3) + 2 frac(e^(log^2(x)))(x^3) * [ 12 frac(log^2(x))(x) – 12 frac(log(x))(x) + 8/x ]$
Semplifichiamo, effettuando anche raccoglimenti:
$ [2 frac(e^(log^2(x)))(x^4) * (2log(x) – 3) ] * ( 4 log^3(x) – 6 log^2(x) + 8 log(x) – 3) + 2 frac(e^(log^2(x)))(x^4) * [ 12 log^2(x) – 12 log(x) + 8 ] = $
$ 2 frac(e^(log^2(x)))(x^4) * [ (2log(x) – 3) * ( 4 log^3(x) – 6 log^2(x) + 8 log(x) – 3) + (12 log^2(x) – 12 log(x) + 8) ] = $
$ 2 frac(e^(log^2(x)))(x^4) * [ 8 log^4(x) – 12 log^3(x) + 16 log^2(x) – 6 log(x) – 12 log^3(x) + 18 log^2(x) – 24 log(x) + 9 + 12 log^2(x) – 12 log(x) + 8 ] = $
$ 2 frac(e^(log^2(x)))(x^4) * [ 8 log^4(x) – 24 log^3(x) + 46 log^2(x) – 42 log(x) + 17 ] $
Calcoliamo il valore della derivata quarta nel punto $ x = 1$:
$ f^(4)(1) = 2 frac(e^(log^2(1)))(1^4) * [ 8 log^4(1) – 24 log^3(1) + 46 log^2(1) – 42 log(1) + 17 ] = 34$
Possiamo infine determinare lo sviluppo di Taylor della funzione di partenza, applicando la formula del polinomio di Taylor al quarto ordine:
$ T_4 (f , 1) = f(1) + f’(1) (x – 1) + frac(f’’(1))(2) (x – 1)^2 + frac(f’’’(1))(6) (x – 1)^3 + frac(f^(4)(1))(24) (x -1)^4 = $
$ T_4 (f , 1) = 1 + 0 (x – 1) + frac(2)(2) (x – 1)^2 + frac(-6)(6) (x – 1)^3 + frac(34)(24) (x – 1)^4 = $
$ 1 + (x – 1)^2 – (x – 1)^3 + frac(17)(12) (x – 1)^4 $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Calcolare lo sviluppo di Taylor della seguente funzione nel punto $x=0$ fino al quinto ordine: $f(x)=3x cos(2x)+6 log(1+x^3)$
Per risolvere l’esercizio, possiamo avvalerci degli sviluppi fondamentali delle funzioni coseno e logaritmo; cominciamo dalla funzione coseno, che ha il seguente sviluppo:
$ cos(z) = 1 – frac(z^2)(2) + frac(z^4)(24) – … + frac((-1)^n z^(2n))((2n)!) + o(z^(2n)) $
In questo caso, poiché l’argomento del coseno è $2x$, dobbiamo operare la sostituzione $ z = 2x$, tenendo presente che per $x to 0$ si ha che $2x = x$, e quindi $o(z) = o(x)$; sapendo che il termine coseno è moltiplicato per un fattore x di primo grado, possiamo fermare lo sviluppo del coseno al grado 4:
$ cos(2x) = 1 – frac((2x)^2)(2) + frac((2x)^4)(24) + o((2x)^(4)) $
Moltiplicando per il fattore $3x$ si ottiene:
$ 3x * cos(2x) = 3x [1 – frac((2x)^2)(2) + frac((2x)^4)(24) + o((2x)^(4))] = $
$ 3x [1 – frac(4x^2)(2) + frac( 16 x^4)(24) + o(x^4)] = 3x [1 – 2x^2 + 2/3 x^4 + o(x^4)] = $
$ 3x – 6x^3 + 2 x^5 + o(x^5) $
Applichiamo lo stesso ragionamento per la seconda parte della funzione, ricordando che lo sviluppo fondamentale della funzione logaritmica è il seguente:
$ log(1+z) = z – frac(z^2)(2) + frac(z^3)(3) + … + (-1)^(n+1) frac(z^n)(n) + o(z^n) $
In questo caso occorre applicare la sostituzione $ z = x^3$, quindi, per raggiungere un quinto grado complessivo, sarà sufficiente fermare lo sviluppo della funzione logaritmo al secondo grado:
$ log(1+z) = z – frac(z^2)(2) + o(z^2) $
Applichiamo la sostituzione:
$ log(1+x^3) = x^3 – frac((x^3)^2)(2) + o((x^3)^2) = x^3 – frac(x^6)(2) + o(x^6) $
Ricordiamo che nella funzione il logaritmo era moltiplicato per un fattore:
$ 6 log(1+x^3) = 6 x^3 – 3 x^6 + o(x^6) $
Possiamo procedere ora con lo sviluppo finale della funzione di partenza:
$ f(x) = 3x cos(2x) + 6 log(1+x^3) = 3x – 6x^3 + 2 x^5 + o(x^5) + 6 x^3 – 3 x^6 + o(x^6) $
Come sappiamo, gli infinitesimi di ordine maggiore vengono inglobati da quelli di ordine minore, quindi in questo caso le potenze di 6 verranno inglobate all’interno di $o(x^5)$:
$ f(x) = 3x – 6x^3 + 2 x^5 + o(x^5) + 6 x^3 = 3x + 2 x^5 + o(x^5) $
Potrebbe interessarti anche
- Tavole degli sviluppi di Taylor
- Esercizi svolti su vari argomenti di Analisi (videolezioni).
Risolvere la seguente equazione con numeri complessi: $ z^3 = 1$
Per risolvere un’equazione di questo tipo dobbiamo procedere considerando la rappresentazione esponenziale dei numeri complessi.
Un numero complesso $z$ può essere scritto in questo modo:
$ z = rho e^(i theta)$
dove $rho$ rappresenta il modulo di $z$, mentre $theta$ è un angolo che rappresenta l’argomento del numero complesso.
L’angolo $theta$ servirà per determinare la posizione delle soluzioni sulla circonferenza goniometrica; ricordiamo, infatti, che vale la seguente uguaglianza:
$ e^(i theta) = cos(theta) + i sin(theta) $
La nostra equazione, quindi, può essere espressa in una nuova forma, più facilmente risolvibile:
$ (rho e^(i theta))^3 = 1 to rho^3 e^( 3i theta) = 1 $
Notiamo che, affinché l’uguaglianza sia verificata, è necessario che $ rho = 1$ e che $ e^(i theta) = e^0 = 1$.
$ e^( 3i theta) = e^(0 + 2kπ) = 1$
Possiamo quindi impostare il seguente sistema:
$ {(rho^3 = 1),(3 theta = 0 + 2k pi):} $
Nella risoluzione dell’equazione dobbiamo tener conto del fatto che, poiché l’esponente di $z$ è 3, avremo esattamente tre soluzioni; ciò significa che i valori che può assumere il coefficiente $k$ sono $ 0, 1, 2$.
Dalla prima equazione risulta evidente che deve essere $ rho = 1$.
Risolviamo ora la seconda equazione; ricordiamo che sono validi tutti gli angoli $theta$ multipli di $360°$:
$ e^( 3i theta) = e^(0) to 3theta = 2kπ $
Quindi:
$ theta = frac(2kπ)(3) $
Determiniamo i tre angoli che individuano le tre soluzioni dell’equazione:
$ k = 0 to theta = 0 $
$ k = 1 to theta = frac(2π)(3) $
$ k = 2 to theta = frac(4π)(3) $
Ora dobbiamo scrivere i numeri complessi $ z_1$ , $ z_2$, $ z_3$ nella forma $ a + ib$.
Per farlo, ricorriamo alla rappresentazione trigonometrica dei numeri complessi, ovvero sfruttiamo l’uguaglianza:
$ z = e^(i theta) = cos(theta) + i sin(theta) $
Nel primo caso abbiamo:
$ z_1 = cos(0) + i sin(0) = 1 $
Nel secondo caso:
$ z_2 = cos(frac(2π)(3)) + i sin(frac(2π)(3)) = -1/2 + frac(sqrt3)(2) i $
E nell’ultimo caso:
$ z_3 = cos(frac(4π)(3)) + i sin(frac(4π)(3)) = -1/2 – frac(sqrt3)(2) i $
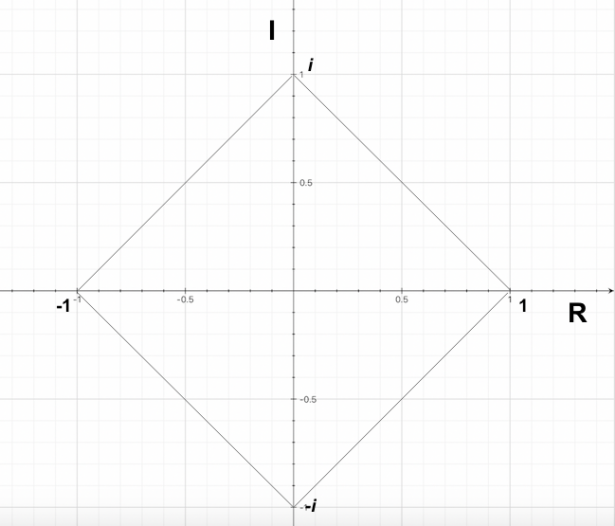
Come possiamo notare, le soluzioni sono una reale e due complesse coniugate; rappresentando le soluzioni ottenute su una circonferenza goniometrica possiamo notare che esse individuano i vertici di un triangolo equilatero.
Risolvere la seguente equazione con numeri complessi: $ z^4 = 1$
Per risolvere un’equazione di questo tipo dobbiamo procedere considerando la rappresentazione esponenziale dei numeri complessi.
Un numero complesso $z$ può essere scritto in questo modo:
$ z = rho e^(i theta)$
dove $ro$ rappresenta il modulo di $z$, mentre $theta$ è un angolo che rappresenta l’argomento del numero complesso.
L’angolo $theta$ servirà per determinare la posizione delle soluzioni sulla circonferenza goniometrica; ricordiamo, infatti, che vale la seguente uguaglianza:
$ e^(i theta) = cos(theta) + i sin(theta) $
La nostra equazione, quindi, può essere espressa in una nuova forma, più facilmente risolvibile:
$ (rho e^(i theta))^4 = 1 to rho^4 e^( 4i theta) = 1 $
Notiamo che, affinché l’uguaglianza sia verificata, è necessario che $ ro = 1$ e che $ e^(i theta) = e^0 = 1$.
$ e^( 4i theta) = e^(0) = 1$
Possiamo quindi impostare il seguente sistema:
$ {(rho^4= 1), (4 theta = 0 + 2k pi):} $
Nella risoluzione dell’equazione dobbiamo tener conto del fatto che, poiché l’esponente di $z$ è 4, avremo esattamente quattro soluzioni; ciò significa che i valori che può assumere il coefficiente $k$ sono $ 0, 1, 2, 3$.
Dalla prima equazione risulta evidente che deve essere $ rho = 1$.
Risolviamo ora la seconda equazione; ricordiamo che sono validi tutti gli angoli $theta$ multipli di $360°$:
$ e^( 4i theta) = e^(0) to 4theta = 2kπ $
Quindi:
$ theta = frac(2kπ)(4) = frac(kπ)(2) $
Determiniamo i tre angoli che individuano le tre soluzioni dell’equazione:
$ k = 0 to theta = 0 $
$ k = 1 to theta = frac(π)(2) $
$ k = 2 to theta = π $
$ k = 3 to theta = frac(3π)(2) $
Ora dobbiamo scrivere i numeri complessi $ z_1$ , $ z_2$, $ z_3$ e $ z_4$ nella forma $ a + ib$.
Per farlo, ricorriamo alla rappresentazione trigonometrica dei numeri complessi, ovvero sfruttiamo l’uguaglianza:
$ z = e^(i theta) = cos(theta) + i sin(theta) $
Nel primo caso abbiamo:
$ z_1 = cos(0) + i sin(0) = 1 $
Nel secondo caso:
$ z_2 = cos(frac(π)(2)) + i sin(frac(π)(2)) = i $
Nel terzo caso:
$ z_3 = cos(π) + i sin(π) = -1 $
Infine, la quarta soluzione è:
$ z_3 = cos(frac(3π)(2)) + i sin(frac(3π)(2)) = -i $
Come possiamo notare, le soluzioni sono due reali e due complesse coniugate; rappresentando le soluzioni ottenute su una circonferenza goniometrica possiamo notare che esse individuano i vertici di un quadrato.
Potrebbe interessarti anche
- Numeri complessi in forma algebrica (videolezione)
- Appunti sui numeri complessi
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = |x+1| + x + log(frac(2x+1)(x-1)) $
Cominciamo lo studio di funzione determinando il dominio della funzione; poiché è presente una funzione logaritmica, dobbiamo imporre che il suo argomento sia maggiore di zero:
$frac(2x+1)(x-1) > 0$
$2x +1 > 0$
$x-1 > 0$
Dallo studio del segno si ottengono i seguenti intervalli: $ x<-1/2 vee x > 1 $
Quindi abbiamo:
$ D = (-oo ; -1/2) uu (1 ; +oo) $.
In questo caso, quindi, la funzione non presenta nessuna intersezione con gli assi, in quanto tutti i punti possibili sono comunque esclusi dal dominio.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = |-x+1| – x + log(frac(-2x+1)(-x-1)) $
La funzione quindi non è ne pari ne dispari.
Passiamo alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo dal limite a $+oo$:
$ lim_(x to +oo) |x+1| + x + log(frac(2x+1)(x-1)) $
In questo intorno, possiamo assumere che $ |x+1| = x + 1$, quindi:
$ lim_(x to +oo) |x+1| + x + log(frac(2x+1)(x-1)) = $
$lim_(x to +oo) x+1 + x + log(frac(2x+1)(x-1)) =$
$lim_(x to +oo) 2x + 1 + log(frac(2x+1)(x-1)) = +oo $
La funzione, quindi, non presenta asintoti orizzontali destri.
Studiamo il comportamento a $- oo$ ; in questo caso si avrà $ |x+1| = – x – 1$:
$ lim_(x to -oo) |x+1| + x + log(frac(2x+1)(x-1)) = $
$lim_(x to -oo) -x-1 + x + log(frac(2x+1)(x-1)) =$
$ lim_(x to -oo) – 1 + log(frac(2x+1)(x-1)) = log(2) – 1 $
Di conseguenza, la retta di equazione $y = log(2) – 1$ è un asintoto orizzontale sinistro per la funzione.
Poiché la funzione presenta solo un asintoto orizzontale sinistro, “a destra” potrebbe essere presente un asintoto obliquo; in tal caso, il coefficiente angolare di tale asintoto è dato da un valore finito di tale limite:
$ m = lim_(x to +oo) frac(f(x))(x) = lim_(x to +oo) 2 + 1/x + frac(log(frac(2x+1)(x-1)))(x) = 2$
Avendo ottenuto un valore finito per $m$, cerchiamo un eventuale $q$:
$ q = lim_(x to +oo) [f(x) – mx] = $
$lim_(x to +oo) 2x + 1 + log(frac(2x+1)(x-1)) – 2x = 1 + log(2) $
Possiamo concludere, quindi, che la retta $ y = 2x + 1 + log(2)$ è un asintoto obliquo destro per la funzione.
Vediamo ora cosa accade quando la funzione si avvicina ai punti che sono esclusi dal dominio; in particolare, risolviamo i seguenti limiti:
$ lim_(x to -1/2 ^-) |x+1| + x + log(frac(2x+1)(x-1)) = $
$lim_(x to -1/2 ^-) x+1 + x + log(frac(2x+1)(x-1)) =$
$ lim_(x to -1/2 ^-) 2x + 1 + log(frac(2x+1)(x-1)) = -oo $
La retta $ x = -1/2$ è quindi asintoto verticale per la funzione.
$ lim_(x to 1^+) |x+1| + x + log(frac(2x+1)(x-1)) = $
$lim_(x to 1^+) x+1 + x + log(frac(2x+1)(x-1)) =$
$lim_(x to 1^+) 2x + 1 + log(frac(2x+1)(x-1)) = +oo $
Anche la retta $ x = 1$ è asintoto verticale per la funzione.
Cerchiamo eventuali punti di massimo o minimo studiando la derivata prima; distendiamo i casi $x > -1$ e $x < – 1$; nel primo caso si ha:
$ f’(x) = 2 + frac(x-1)(2x+1) * frac(2(x-1) – 2x – 1)((x-1)^2) = $
$2 – frac(3)((2x+1)(x-1)) = $ $ frac(4x^2 – 2x – 5)( (2x+1)(x-1) ) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to frac(4x^2 – 2x – 5)( (2x+1)(x-1) ) = 0 $
$ 4x^2 – 2x – 5 = 0 to x = frac(1+sqrt(21))(4) vee x = frac(1-sqrt(21))(4) $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to frac(4x^2 – 2x – 5)( (2x+1)(x-1) ) > 0 $
$ 4x^2 – 2x – 5 > 0 $
$ (2x+1)(x-1) > 0 $
Dallo studio del segno e tenendo conto che siamo nel caso in cui $x > -1 $ otteniamo i seguenti intervalli: $ ( – 1 , frac(1-sqrt(21))(4) ) uu ( frac(1+sqrt(21))(4) ; +oo ) $; la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che il punto individuato da $ x = frac(1+sqrt(21))(4) $ è un punto di minimo relativo per la funzione, mentre il punto individuato da $ x = frac(1-sqrt(21))(4) $ è un punto di massimo relativo per la funzione.
Passiamo ora al caso $ x < – 1$:
$ f’(x) = frac(x-1)(2x+1) * frac(2(x-1) – 2x – 1)((x-1)^2) = frac(3)((2x+1)(x-1)) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to frac(3)((2x+1)(x-1)) = 0 $
In questo caso la derivata prima non si annulla in nessun punto; dallo studio del segno si trova il seguente intervallo: $ (-1/2 , 1) $
Quindi, nell’intervallo che stiamo considerando, la derivata sarà sempre negativa, di conseguenza la funzione sarà decrescente nell’intervallo $ x < – 1$.
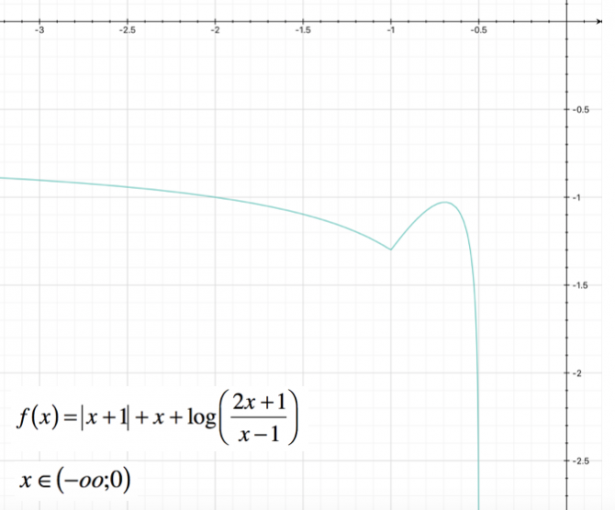
In questo caso, il calcolo della derivata seconda si rivela troppo complesso; possiamo comunque tracciare il grafico approssimativo della funzione:
Nell’intervallo $ (-oo ; 0) $ si avrà un grafico di questo tipo:
Mentre nell’intervallo $ ( 0 ; +oo ) $ si avrà un grafico di questo tipo:
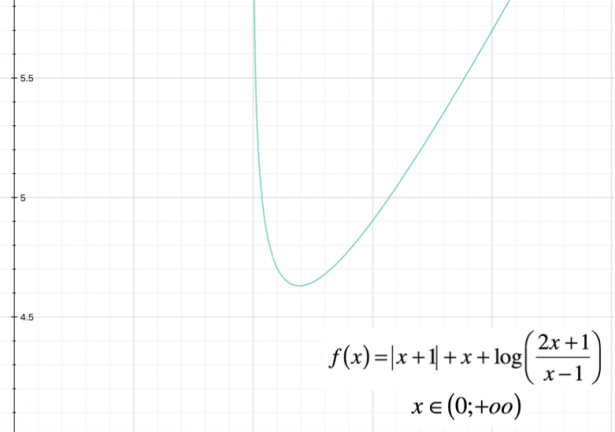
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = arctan( log( frac(x)( (x+3) * |x+4| ) ) ) $
La funzione arcotangente è definita su tutto R, quindi le uniche condizioni che dobbiamo imporre riguardano l’argomento del logaritmo. Poniamo, quindi, tale argomento maggiore di zero:
$frac(x)( (x+3) * |x+4| ) > 0$
$x > 0$
$x+3 > 0$
$|x+4|>0$
Dallo studio del segno si ottengono i seguenti intervalli: $ x<-3 vee x > 0 , x != -4$
Quindi abbiamo:
$ D = (-oo ; -4) uu (-4 ; -3) uu (0 ; +oo) $.
Per semplicità, nello svolgimento dei prossimi calcoli è conveniente eliminare il valore assoluto, e per farlo ricordiamo la proprietà dei valori assoluti per cui:
$ |x| = x text( se ) x >= 0$
$ |x| = -x text( se ) x < 0$
In questo caso, quindi, possiamo assumere:
$ f(x) = arctan( log( frac(x)( (x+3) * (x+4) ) ) ) text(se) x > -4 $
$ f(x) = arctan( log( frac(x)( (x+3) * (-x-4) ) ) ) text(se) x < -4 $
Determiniamo ora i punti di intersezione con gli assi: $ f(x) _|_ (y = 0)$
Se $x > -4$:
$arctan( log( frac(x)( (x+3) * (x+4) ) ) ) = 0 to log( frac(x)( (x+3) * (x+4) ) ) = 0$
$ frac(x)( (x+3) * (x+4) ) = 1 to frac(x – x^2 – 3x – 4x – 12)( (x+3) * (x+4) ) = 0$
$ x^2 + 6x + 12 = 0$
L’equazione è priva di soluzioni reali (delta negativo), quindi la funzione non ha punti di intersezione con l’asse x per $ x > -4$.
Se $x < -4$:
$arctan( log( frac(x)( (x+3) * (-x-4) ) ) ) = 0 to log( frac(x)( (x+3) * (-x-4) ) ) = 0$
$ frac(x)( (x+3) * (-x-4) ) = 1 to frac(x + x^2 + 3x + 4x + 12)( (x+3) * (-x-4) ) = 0$
$ x^2 + 8x + 12 = 0 to x = -6 vee x = -2$
Possiamo accettare come soluzione solo $ x = -6$; di conseguenza, il punto di intersezione è $ ( -6 ; 0 ) $.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = arctan( log( frac(-x)( (-x+3) * |-x+4| ) ) ) $
La funzione quindi non è ne pari ne dispari.
Determiniamo gli intervalli in cui la funzione è positiva; per $x > -4$ si ha:
$ arctan( log( frac(x)( (x+3) * (x+4) ) ) ) > 0 to log( frac(x)( (x+3) * (x+4) ) ) > 0$
$ frac(x)( (x+3) * (x+4) ) > 1 to frac(x-x^2 – 7x – 12)( (x+3) * (x+4) ) > 0 to $
$ frac( -x^2 – 6x – 12)( (x+3) * (x+4) ) > 0 $
Tale disequazione è verificata per valori di x nell’intervallo $(-4;-3)$; la funzione, quindi, è positiva in tale intervallo.
Vediamo ora il caso $x < -4$ si ha:
$ arctan( log( frac(x)( (x+3) * (-x-4) ) ) ) > 0 to log( frac(x)( (x+3) * (-x-4) ) ) > 0$
$ frac(x)( (x+3) * (-x-4) ) > 1 to frac(x)( (x+3) * (x+4) ) < -1 to $
$ frac(x+x^2 + 7x + 12)( (x+3) * (x+4) ) < 0 to frac(x^2 + 8x + 12)( (x+3) * (x+4) ) < 0 $
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo dal limite a $+oo$:
$ lim_(x to +oo) arctan( log( frac(x)( (x+3) * |x+4| ) ) ) = lim_(x to +oo) arctan( log( frac(x)( (x+3) * (x+4) ) ) ) = – π/2$
Passiamo ora al limite a $-oo$ :
$ lim_(x to +oo) arctan( log( frac(x)( (x+3) * |x+4| ) ) ) = lim_(x to +oo) arctan( log( frac(x)( (x+3) * (-x-4) ) ) ) = – π/2$
Quindi, la retta di equazione $ y = – π/2$ è asintoto orizzontale (destro e sinistro) per la funzione.
Studiamo ora il comportamento della funzione quando si avvicina ai punti che sono esclusi dal dominio; cominciamo con il caso $ x to 3^-$:
$ lim_(x to -3^-) arctan( log( frac(x)( (x+3) * |x+4| ) ) ) = lim_(x to -3^-) arctan( log( frac(x)( (x+3) * (x+4) ) ) ) = π/2$
Allo stesso modo, per $x to 0^+$:
$ lim_(x to 0^+) arctan( log( frac(x)( (x+3) * |x+4| ) ) ) = lim_(x to 0^+) arctan( log( frac(x)( (x+3) * (x+4) ) ) ) = -π/2$
Infine, per $ x to -4$ si ha:
$ lim_(x to -4^+) arctan( log( frac(x)( (x+3) * |x+4| ) ) ) = lim_(x to -4^+) arctan( log( frac(x)( (x+3) * (x+4) ) ) ) = π/2$
$ lim_(x to -4^-) arctan( log( frac(x)( (x+3) * |x+4| ) ) ) = lim_(x to -4^-) arctan( log( frac(x)( (x+3)*(-x-4) ) ) ) = π/2$
La funzione, quindi, non presenta asintoti verticali.
Cerchiamo eventuali punti di massimo o minimo studiando la derivata prima:
$ f’(x) = frac( frac(x^2 + 7x + 12 – 2x^2 – 7x)((x^2 + 7x + 12)^2) )( 1 + log^2(frac(x)(x^2 + 7x + 12)) ) * frac(x^2 + 7x + 12)(x) = $
$ frac(1)( 1 + log^2(frac(x)(x^2 + 7x + 12)) ) * frac(12 – x^2)( x^3 + 7x^2 + 12x) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to frac(1)( 1 + log^2(frac(x)(x^2 + 7x + 12)) ) * frac(12 – x^2)( x^3 + 7x^2 + 12x) = 0 $
$ 12 – x^2 = 0 to x^2 = 12 to x = pm sqrt(12) $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to frac(1)( 1 + log^2(frac(x)(x^2 + 7x + 12)) ) * frac(12 – x^2)( x^3 + 7x^2 + 12x) > 0 $
$ 1 + log^2(frac(x)(x^2 + 7x + 12)) > 0 $
$ 12 – x^2 > 0 $
$ x^3 + 7x^2 + 12x > 0 $
Dallo studio del segno si ottengono i seguenti intervalli: $ ( – oo , – 4 ) U ( -sqrt(12) ; -3) U ( 0 ; sqrt(12) ) $; la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che il punto individuato da $ x = – sqrt(12) $ è un punto di minimo relativo per la funzione, mentre il punto individuato da $ x = sqrt(12) $ è un punto di massimo relativo per la funzione.
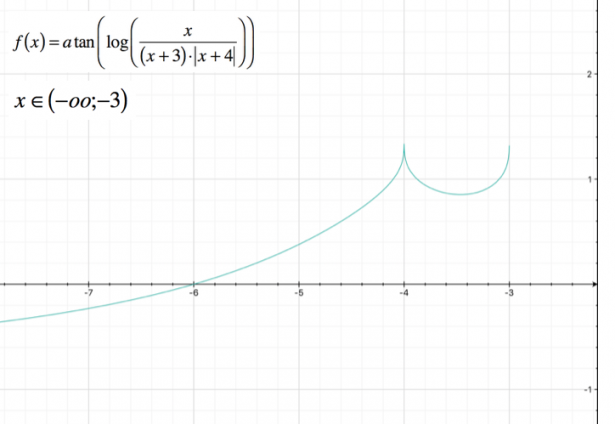
In questo caso, il calcolo della derivata seconda si rivela troppo complesso; possiamo comunque tracciare il grafico approssimativo della funzione.
Nell’intervallo $ (-oo ; -3) $ si avrà un grafico di questo tipo:
Mentre nell’intervallo $ (0 ; +oo) $ si avrà:
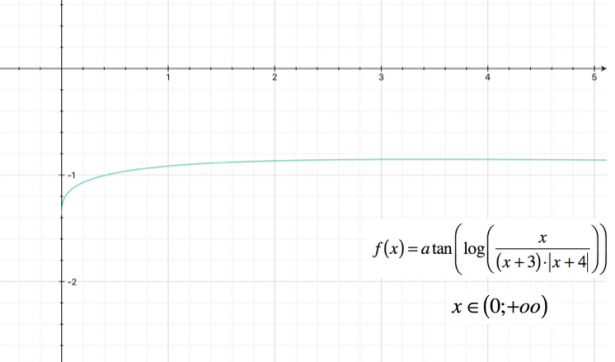
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = arcsin(frac(x+1)(x-1)) $
La funzione in questione è una funzione trigonometrica, e in particolare è la funzione inversa della funzione seno. In questo caso, sapendo che il seno di un angolo è sempre un valore compreso tra -1 e 1, possiamo imporre che:
$ -1 <= frac(x+1)(x-1) <= 1 $
Per poter risolvere questa disequaizone dobbiamo imporre un sistema:
$ {(frac(x+1)(x-1) <= 1),(frac(x+1)(x-1) >= -1):} $
Ovvero:
${(frac(x+1 – x + 1)(x-1) <= 0),(frac(x+1+ x – 1 )(x-1) >= 0):}$
${(frac(2)(x-1) <= 0),(frac(2x)(x-1) >= 0):}$
Risolvendo le due disequazioni si ottiene il seguente sistema:
$ {(x <=1),(x <= 0 V x > 1):} $
Le soluzioni del sistema sono rappresentate dal seguente intervallo $ ( -oo ; 0 ] $, che rappresenta il dominio della funzione.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ (x = 0) $
$ f(0) = arcsin(frac(0+1)(0-1)) = arcsin(-1) = – π/2 $
Il punto individuato è $ ( 0 ; -π/2 ) $.
$ f(x) _|_ (y = 0) $
$ f(x) = 0 to arcsin(frac(x+1)(x-1)) = 0 $
$ frac(x+1)(x-1) = 0 to x + 1 = 0 to x = – 1 $
Otteniamo il punto $ ( -1 ; 0 ) $.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = arcsin(frac(-x+1)(-x-1)) $
La funzione quindi non è ne pari ne dispari.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso il limite a $-oo$:
$ lim_(x to -oo) arcsin(frac(x+1)(x-1)) $
Non vi sono in questo limite forme di indecisione, in quanto la frazione che è argomento del’arcoseno presenta numeratore e denominatore dello stesso grado; si ha quindi:
$ lim_(x to -oo) arcsin(frac(x+1)(x-1)) = arcsin(1) = π/2 $
Ha come asintoto orizzontale la retta di equazione $ y = π/2$.
Studiamo ora il comportamento della derivata prima della funzione:
$ f’(x) = frac(1)(sqrt(1 – (frac(x+1)(x-1))^2) ) = frac(1)(sqrt(1 – frac((x+1)^2)((x-1)^2)) ) = $
$ frac(1)(sqrt(frac( (x-1)^2 – (x+1)^2)((x-1)^2)) ) = frac( | x – 1| )(sqrt( (x-1)^2 – (x+1)^2) ) =$
$ frac( | x – 1| )(sqrt( x^2 + 1 – 2x – x^2 – 1 – 2x) ) = frac( | x – 1| )(sqrt(- 4x) ) $
Poiché la funzione è definita per $x < 0$, e sapendo che $| x – 1| = x – 1 se x >= 1 $
$| x – 1| = – x + 1 se x < 1$ Possiamo scrivere la derivata prima in questo modo: $ f’(x) = frac( 1 – x )(sqrt(- 4x) ) $ Troviamo i punti in cui la deriva prima si annulla: $ f’(x) = 0 to frac( 1 – x )(sqrt(- 4x) ) = 0 $ $ 1 – x = 0 to x = 1 $ Tale punto, però, non appartiene al dominio della funzione; studiamo il segno della derivata prima: $ f’(x) > 0 to frac( 1 – x )(sqrt(- 4x) ) > 0 $
$ 1 – x > 0 $
$ sqrt(- 4x) > 0 $
Dallo studio del segno si ottengono i seguenti intervallo: $ ( 0; +oo ) $; tale intervallo non appartiene al dominio della funzione e quindi, poiché la derivata prima è negativa nei punti del dominio, sappiamo che la funzione sarà decrescente in tutto il dominio.
Possiamo procedere rappresentando il grafico approssimativo della funzione:
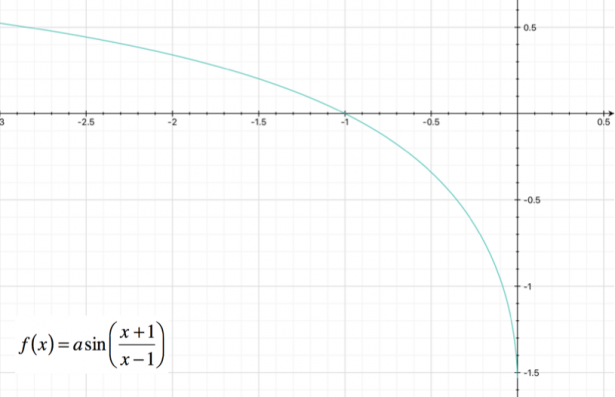
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = x^2 [ log(x/4) – 1]^2 $
Nel caso di funzioni logaritmiche, sappiamo che il dominio corrisponde all’insieme dei numeri reali per i quali l’argomento del logaritmo è positivo:
$ x/4 > 0 to x > 0$
Per cui:
$ D = ( 0 ; +oo)$.
Determiniamo ora i punti di intersezione con l’asse x (con l’asse y non vi sono punti di intersezione, perché i punti per cui x = 0 sono esclusi dal dominio):
$ f(x) _|_ (y = 0) $
$ f(x) = 0 to x^2 [ log(x/4) – 1]^2 = 0 $
$log(x/4) – 1 to log(x/4) = 1 to x/4 = e^1$
$ x/4 = e to x = 4e $
Il punto individuato è $ ( 4e ; 0 ) $.
Quindi la funzione ha un punto di intersezione con l’asse x.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a $+oo$:
$ lim_(x to oo) x^2 [ log(x/4) – 1]^2 $
Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:
$ lim_(x to oo) x^2 [ log(x/4) – 1]^2 = +oo $
La funzione, quindi, non presenta asintoti orizzontali.
Cerchiamo la presenza di eventuali asintoti obliqui:
$ m = lim_(x to oo) frac(f(x))(x) = lim_(x to oo) x [ log(x/4) – 1]^2 = +oo $
Quindi non sono presenti neanche asintoti obliqui.
Studiamo ora il comportamento della funzione quando si avvicina al punto $(0;0)$ (da destra):
$ lim_(x to 0^+) f(x) = lim_(x to 0^+) [ frac(log(x/4) – 1)(x^(-1))]^2 = 0 $
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = 2x (log(x/4) – 1)^2 + x^2 (log(x/4) – 1) * 4/x * 1/4 = (log(x/4) – 1) (2x log(x/4) – 2x + 2x) =$
$ 2x log(x/4) (log(x/4) – 1)$
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to 2x log(x/4) (log(x/4) – 1) = 0 to log(x/4) – 1 = 0 $
$ log(x/4) = 1 to x/4 = e to x = 4e $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to 2x log(x/4) (log(x/4) – 1) > 0 $
$ x > 0 $
$ log(x/4) > 0 to x/4 > 1 to x > 4 $
$ log(x/4) – 1 > 0 to log(x/4) > 1 x/4 > e to x > 4e $
Dallo studio del segno si ottiene: $ ( 0 , 4 ) U ( 4e , +oo) $; la funzione, quindi, è crescente in tale intervallo; nell’intervallo $ ( 4 , 4e )$ la funzione sarà decrescente.
Notiamo, quindi, che il punto $ ( 4e , 0 )$ è un punto di minimo per la funzione.
In questo caso, lo studio della derivata seconda si rileva troppo complesso; possiamo comunque procedere rappresentando il grafico approssimativo della funzione:
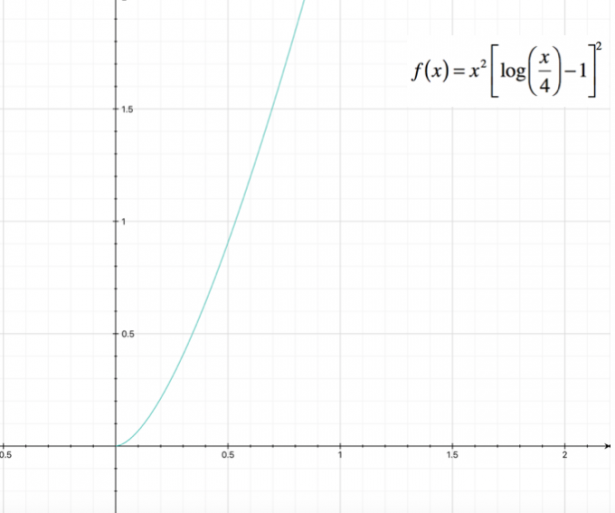
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = \frac{ \root[3]{x}}{x + 1} $
Nel caso di funzioni fratte, nella determinazione del dominio si deve tener conto degli eventuali punti in cui la funzione potrebbe non essere definita, e questi sono i punti per cui il denominatore della funzione si annulla; in questo caso abbiamo:
$ text(Denominatore) = 0 to x + 1 = 0 to x = – 1$
Il dominio della funzione, quindi, è dato dall’insieme dei numeri reali eccetto in valore -1:
$ D = R – {-1}$
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ (x = 0) to f(0) = 0 $
Il punto individuato è quindi $ (0 ; 0) $.
$ f(x) _|_ (y = 0) $
$ f(x) = 0 to \frac{ \root[3]{x}}{x + 1} = 0 to x = 0 $
Il punto individuato è anche in questo caso $ (0 ; 0) $.
La funzione, quindi, passa per l’origine, e non ha altri punti di intersezione con gli assi.
Cerchiamo gli intervalli in cui la funzione è negativa e quelli in cui è positiva:
$ f(x) > 0 to \frac{ \root[3]{x}}{x + 1} > 0 $
Studiando insegno si ottiene $ x < -1 vee x > 0$; la funzione in tale intervallo è positiva, mentre sarà negativa nell’intervallo $ -1 < x < 0$.
Studiamo la parità della funzione; ricordiamo che se $ f(-x) = f(x)$, la funzione è pari, ovvero simmetrica rispetto all’asse y, altrimenti se $ f(-x) = – f(x)$ la funzione è dispari, ovvero simmetrica rispetto all’origine. In questo caso:
$ f(-x) = \frac{ \root[3]{-x}}{-x + 1} = – \frac{ \root[3]{x}}{-x + 1} $
uindi la funzione non è ne pari ne dispari.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso, a $+oo$ e $-oo$:
$ lim_(x to oo) \frac{ \root[3]{-x}}{-x + 1} $
Essendo il denominatore di grado maggiore den numeratore, tale limite vale 0, e questo valore si ha sia per $+oo$ che per $-oo$. Abbiamo, quindi, la presenza di un asintoto orizzontale e, poiché il valore del limite è 0, l’equazione dell’asintoto orizzontale è $ y = 0$, ovvero l’asse x è asintoto orizzontale. Poiché la funzione non è definita in $ x = -1$, in tale punto potrebbe esserci un asintoto verticale; controlliamo quindi la sua eventuale presenza risolvendo i limiti destro e sinistro:
$ lim_(x to -1^+) \frac{ \root[3]{-x}}{-x + 1} , lim_(x to -1^-) \frac{ \root[3]{-x}}{-x + 1} $
Nel primo caso abbiamo:
$ lim_(x to -1^+) \frac{ \root[3]{-x}}{-x + 1} = \frac{-1}{0^+} = – oo $
Mentre nel secondo caso:
$ lim_(x to -1^-) \frac{ \root[3]{-x}}{-x + 1} = \frac{-1}{0^-} = + oo $
Quindi si ha un asintoto verticale sia destro che sinistro di equazione $ x = – 1$.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = frac( 1/3 x^(-2/3) (x + 1) – x^(1/3) )( (x + 1)^2 ) = $
$frac( 1/3 x^(1/3) + 1/3x^(-2/3) – x^(1/3) )( (x + 1)^2 ) = $
$ frac( -2/3 x^(1/3) + 1/3 x^(-2/3) )( (x + 1)^2 ) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to frac( -2/3 x^(1/3) + 1/3 x^(-2/3) )( (x + 1)^2 ) = 0 $
$ 2/3 x^(1/3) = 1/3 x^(-2/3) to frac(2x – 1)(x^(2/3)) = 0 to x = 1/2 $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to frac( -2/3 x^(1/3) + 1/3 x^(-2/3) )( (x + 1)^2 ) > 0 to $
$ frac( -2/3 x + 1/3 )( x^(2/3)(x + 1)^2 ) > 0 to x < 1/2 $
Dallo studio della derivata prima possiamo capire che la funzione sarà crescente per $x<1/2$, quindi necessariamente essa presenterà un massimo (relativo) in $1/2$; in particolare, in tale punto la funzione assume il valore:
$ f(1/2) = \frac{1}{\root[3]{2}} * \frac{1}{3/2} = \frac{ \root[3]{4}}{3} $
Quindi, il punto $ ( \frac{1}{2} ; \frac{ \root[3]{4}}{3} ) $ è un punto di massimo relativo per la funzione.
Possiamo quindi procedere rappresentando il grafico della funzione:
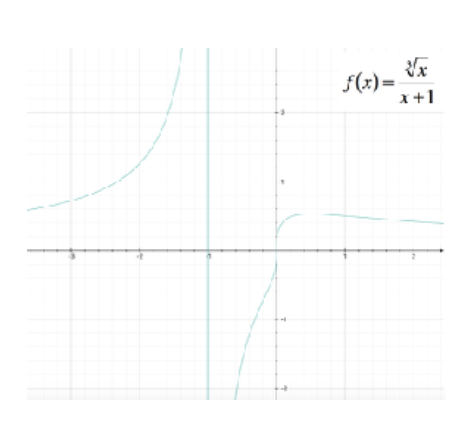
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Giochi di guerra
La teoria dei giochi viene fatta risalire ad un celebre carteggio del 1654 tra Blaise Pascal e Pierre de Fermat, un filosofo e un magistrato entrambi appassionati di matematica. Continua a leggere “Giochi di guerra”
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = x^2 – 3 x^(2/3) $
Nel caso di funzioni esponenziali, sappiamo che il dominio corrisponde a tutto l’insieme dei numeri reali, quindi:
$ D = R $.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ (x = 0) $
$ f(0) = 0^2 – 3 * 0^(2/3) = 0 $
Il punto individuato è $ (0 ; 0) $.
$ f(x) _|_ (y = 0)$
$ f(x) = 0 to x^2 – 3 x^(2/3) = 0 $
$ x^2 = 3 \root[3]{x^2} $
$ x^6 = 27 x^2 to x^2 (x^4 – 27) = 0 $
$ x = +- \root[4]{27} , x = 0 $
I punti individuati sono $ ( \root[4]{27} ; 0 ) $ e $ ( – \root[4]{27} ; 0 ) $.
Quindi la funzione passa per l’origine e ha due punti di intersezione con l’asse x.
Notiamo che $ f(x) = f(-x)$, quindi la funzione è pari, ovvero simmetrica rispetto all’asse y.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso, a $+oo$ e $-oo$:
$ lim_(x to oo) x^2 – 3 x^(2/3) $
Il limite può essere risolto immediatamente: le incognite presenti, infatti, sono di gradi diverso, e nella determinazione del limite si tiene conto di quella di grado più alto; abbiamo, quindi:
$ lim_(x to +oo) x^2 – 3 x^(2/3) = lim_(x to -oo) x^2 – 3 x^(2/3) = + oo $
La funzione, quindi, non presenta asintoti né orizzontali né verticali.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = 2x – 3*2/3 x^(-1/3) = 2x – frac(2)(x^(1/3)) = 2frac(x^(2/3) – 1)(x^(1/3)) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to 2frac(x^(2/3) – 1)(x^(1/3)) = 0 to x^(2/3) = 1 to x = pm 1 $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to 2frac(x^(2/3) – 1)(x^(1/3)) > 0 $
$ N > 0 to x^(2/3) – 1 > 0 to x^2 > 1 to -1 < x < 1$
$ D > 0 to x^(1/3) > 0 to x > 0 $
Dallo studio del segno si ottiene: $ (-1 , 0) uu ( 1 , +oo) $; la funzione, quindi, è crescente in tale intervallo; poiché la funzione è pari, possiamo assumere che essa sia decrescente negli intervalli “speculari”: $ (-oo , -1) uu ( 0 , 1) $.
Notiamo, quindi, che i punti in cui $ x = -1$ e $ x = 1$ sono punti di minimo per la funzione.
Poiché la funzione non presenta asintoti orizzontali, cerchiamo la eventuale presenza di asintoti obliqui:
$ lim_(x to 0) frac(f(x) )(x) = frac(x^2 – 2 x^(2/3))(x) = oo $
Essendo tale limite infinito, la funzione non presenta asintoti obliqui.
Passiamo allo studio della derivata seconda:
$ f’’(x) = 2 * frac(2/3 x^(-1/3) * x^(1/3) – (x^(2/3) – 1) * 1/3 x^(-2/3) )(x^(2/3)) = $
$ 2 * frac(2/3 – 1/3 + 1/3 x^(-2/3) )(x^(2/3)) = $
$ 2/3 frac(1 + x^(-2/3) )(x^(2/3)) $
Troviamo i punti in cui la deriva seconda si annulla:
$ f’’(x) = 0 to 2/3 frac(1 + x^(-2/3) )(x^(2/3)) = 0 to 1 + x^(-2/3) = 0 $
La quantità al numeratore è sempre positiva, quindi la derivata seconda non si annulla mai; ciò significa che , essendo positiva la derivata seconda, la funzione presenta una concavità verso l’alto su tutto $R$.
Possiamo quindi procedere rappresentando il grafico della funzione:
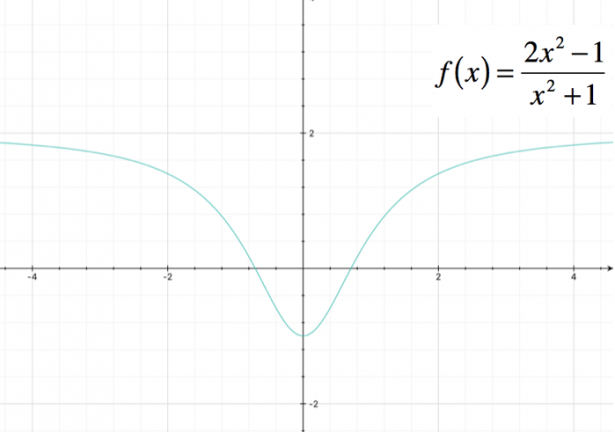
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = 3x – log(| x^2 + x – 2|) $
La funzione si presenta come la somma di due funzioni, di cui una lineare e l’altra logaritmica; sappiamo che l’argomento del logaritmo deve essere un valore positivo, e poiché in questo caso l’argomento è un valore assoluto, dobbiamo escludere dal dominio della funzione solo i valori che annullano tale modulo:
$ x^2 + x – 2 = 0 to x = 1 uu x = -2 $
Quindi abbiamo:
$ D = R – { 1 ; -2} $.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ x = 0$
$ f(0) = 3*0 – log(| 0^2 + 0 – 2|) = – log(2) $
Il punto individuato è $ ( 0 ; – log(2) ) $.
L’intersezione della funzione con l’asse x non può essere calcolata con metodi analitici, in quanto so dovrebbe risolvere un’equazione del tipo:
$ 3x = log(| x^2 + x – 2|) $
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = 3(-x) – log(| (-x)^2 – x – 2|) $
La funzione quindi non è ne pari ne dispari.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo dal limite a $+oo$:
$ lim_(x to +oo) 3x – log(| x^2 + x – 2|) $
Dalle proprietà dei valori assoluti, sappiamo che:
$ | x^2 + x – 2| = x^2 + x – 2 $ quando $ x^2 + x – 2 >= 0 $ cioè $ x < -2 V x > 1$
Quindi, per l’intorno che stiamo studiando, possiamo scrivere il limite nel seguente modo:
$ lim_(x to +oo) 3x – log(| x^2 + x – 2|) = lim_(x to +oo) 3x – log( x^2 + x – 2) $
Poiché il limite si presenta in una forma indeterminata, procediamo nel seguente modo: mettiamo in evidenza $x^2$ nell’argomento del logaritmo:
$ lim_(x to +oo) 3x – log( x^2 + x – 2) = lim_(x to +oo) 3x – log( x^2 ( 1 + 1/x – 2/x^2) $
Applicando le proprietà dei logaritmi si ottiene:
$ lim_(x to +oo) 3x – log( x^2 ( 1 + 1/x – 2/x^2) = $
$lim_(x to +oo) 3x – log(x^2) – log( 1 + 1/x – 2/x^2) = $
$ lim_(x to +oo) 3x – 2log(x) – log( 1 + 1/x – 2/x^2) $
Ora mettiamo in evidenza $x$ fra tutti i termini:
$ lim_(x to +oo) 3x – 2log(x) – log( 1 + 1/x – 2/x^2) = $
$lim_(x to +oo) x [3 – frac(2log(x))(x) – frac(log( 1 + 1/x – 2/x^2))(x)] $
In questo modo possiamo calcolare il valore del limite: infatti, le frazioni che compaiono possono essere risolte facilmente, perché presentano tutte un denominatore che è un infinito di ordine maggiore del numeratore; di conseguenza, tali frazioni tendono a 0 per $x to +oo$.
Abbiamo quindi il risultato seguente:
$ lim_(x to +oo) x [3 – frac(2log(x))(x) – frac(log( 1 + 1/x – 2/x^2))(x)] = +oo $
La funzione, quindi, non presenta asintoti orizzontali destri.
Studiamo ora l’andamento della funzione a $ – oo$. Con un ragionamento analogo al precedente si ha:
$ lim_(x to -oo) 3x – log(| x^2 + x – 2|) = lim_(x to -oo) 3x – log( -x^2 – x + 2) $
Effettuiamo gli stessi raccoglimenti per eliminare la forma indeterminata:
$ lim_(x to -oo) 3x – log( x^2 ( -1 – 1/x + 2/x^2) = $
$lim_(x to -oo) 3x – log(x^2) – log( -1 – 1/x + 2/x^2) = $
$ lim_(x to -oo) 3x – 2log(-x) – log( -1 – 1/x + 2/x^2) = $
$lim_(x to +oo) x [3 – frac(2log(x))(x) – frac(log( -1 – 1/x + 2/x^2))(x)] = -oo$
La funzione, quindi, non presenta neanche asintoti orizzontali sinistri.
Non avendo asintoti orizzontali, la funzione potrebbe presentare degli asintoti obliqui; ricerchiamo, se esiste finito, il coefficiente angolare del possibile asintoto:
$ m = lim_(x to oo) frac(f(x))(x) = lim_(x to oo) 3 – frac(log(| x^2 + x – 2|))(x) $
Scomponiamo il logaritmo fattorizzando il suo argomento e applicando le proprietà algebriche dei logaritmi:
$ m = lim_(x to oo) 3 – frac( log(|(x-1)(x+2)|) )(x) = $
$lim_(x to oo) 3 – frac( log(| x-1|) + log(| x+2|) )(x) = $
$ lim_(x to oo) 3 – frac( log(| x-1|) )(x) – frac( log(| x+2|) )(x) $
Le frazioni presenti hanno un denominatore che è un infinito di ordine maggiore del numeratore; di conseguenza, si ha:
$ lim_(x to oo) 3 – frac( log(| x-1|) )(x) – frac( log(| x+2|) )(x) = 3$
Poiché abbiamo ottenuto un valore finito per $m$, cerchiamo ora il valore di $q$:
$ q = lim_(x to oo) [ f(x) – mx] = $
$lim_(x to oo) [ 3x – log(| x^2 + x – 2|) – 3x] = $
$ lim_(x to oo) [ – log(| x^2 + x – 2|) ] = -oo$
Poiché $q$ assume un valore non finito, possiamo affermare che non esistono asintoti obliqui.
Non essendo definita in $ x = 1$ e $ x = -2$, studiamo il comportamento della funzione quando si avvicina a tali valori:
$ lim_(x to 1) 3x – log(| x^2 + x – 2|) $
Possiamo scomporre il logaritmo fattorizzando il trinomio notevole che ha come argomento, e applicando poi le proprietà dei logaritmi:
$ lim_(x to 1) 3x – log(| x^2 + x – 2|) = lim_(x to 1) 3x – log(|(x-1)(x+2)|) = $
$ lim_(x to 1) 3x – log(| x-1|) – log(| x+2|) $
Poiché si ha:
$ lim_(x to 1) 3x = 3 $
$ lim_(x to 1) – log(| x-1|) = +oo $
$ lim_(x to 1) – log(| x+2|) = – log(3) $
Il valore del limite sarà: $ lim_(x to 1) 3x – log(| x-1|) – log(| x+2|) = + oo$
Di conseguenza, la funzione presenta un asintoto verticale di equazione $ x = 1$.
Vediamo ora cosa accade per $ x to -2$:
$ lim_(x to -2) 3x – log(| x^2 + x – 2|) = lim_(x to -2) 3x – log(|(x-1)(x+2)|) = $
$ lim_(x to -2) 3x – log(| x-1|) – log(| x+2|) $
In questo caso:
$ lim_(x to -2) 3x = -6 $
$ lim_(x to -2) – log(| x-1|) = – log(3) $
$ lim_(x to -2) – log(| x+2|) = + oo $
E quindi il limite generale vale: $ lim_(x to -2) 3x – log(| x-1|) – log(| x+2|) = +oo$
Abbiamo trovato che anche la retta di equazione $ x = -2$ è asintoto verticale per la funzione.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = 3 – frac(2x + 1)(x^2 + x – 2) = frac(3x^2 + x – 7)(x^2 + x – 2) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to frac(3x^2 + x – 7)(x^2 + x – 2) = 0 $
$ 3x^2 + x – 7 = 0 to x = frac(-1 + sqrt(85))(6) vee x = frac(-1 – sqrt(85))(6) $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to frac(3x^2 + x – 7)(x^2 + x – 2) > 0 $
$ 3x^2 + x – 7 > 0 $
$ x^2 + x – 2 > 0 $
Dallo studio del segno si ottengono i seguenti intervalli: $ ( – oo , -2 ) uu ( frac(-1 – sqrt(85))(6) ; 1) uu ( frac(-1 + sqrt(85))(2) ; +oo ) $; la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che i punti individuati da $ x = frac(-1 – sqrt(85))(6) $ e da $ x = frac(-1 – sqrt(85))(6) $ sono punti di minimo relativo per la funzione.
Calcoliamo ora la derivata seconda della funzione:
$ f’’(x) = frac( (6x + 1)(x^2 + x – 2) – (3x^2 + x – 7) * (2x + 1) )( (x^2 + x – 2)^2 ) = $
$ frac( 6x^3 + x^2 + 6x^2 + x – 12x – 2 – 6x^3 – 3x^2 – 2x^2 – x + 14x + 7 )( (x^2 + x – 2)^2 ) = $
$ frac( 2x^2 + 2x + 5 )( (x^2 + x – 2)^2 ) $
Troviamo i valori di x che annullano la derivata seconda:
$ f’’(x) = 0 to frac( 2x^2 + 2x + 5 )( (x^2 + x – 2)^2 ) = 0 $
$ 2x^2 + 2x + 5 = 0 $
Tale valore non si annulla mai, in quanto il delta è minore di zero; poiché la derivata seconda è sempre positiva, possiamo affermare che la funzione rivolge la concavità verso l’alto in tutto il suo dominio.
Possiamo tracciare il grafico della funzione:
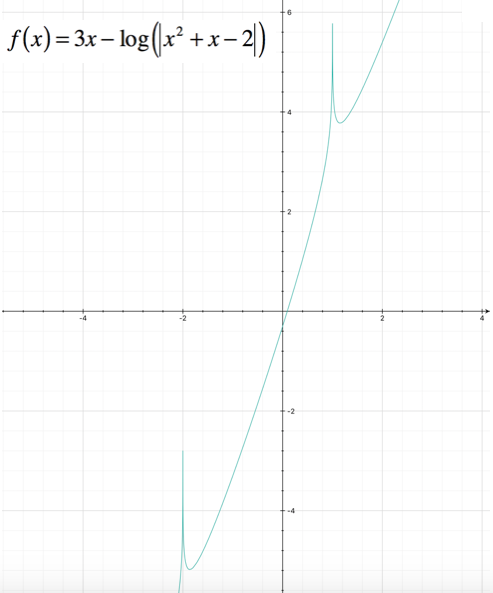
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = (x^2 + x) e^(x+1) $
La funzione si presenta come il prodotto tra due funzioni, di cui una lineare e l’altra esponenziale; in questo caso, quindi, il dominio della funzione è l’insieme dei numeri reali:
$ D = R $.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ (x = 0) $
$ f(0) = (0^2 + 0) e^(0+1) = 0 $
Il punto individuato è $ ( 0 ; 0 ) $.
$ f(x) _|_ (y = 0)$
$ f(x) = 0 to (x^2 + x) e^(x+1) = 0 $
$ x^2 + x = 0 to x(x+1) = 0 to x = 0 V x = -1$
In questo caso abbiamo due punti, di cui uno già individuato in precedenza ($ ( 0 ; 0 ) $), e l’altro $ ( -1 ; 0 ) $.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = ((-x)^2 – x) e^(-x+1) $
La funzione quindi non è ne pari ne dispari.
Cerchiamo gli intervalli in cui la funzione è positiva:
$ f(x) > 0 to (x^2 + x) e^(x+1) > 0 to x^2 + x > 0 $
Poiché l’esponenziale è sempre positivo, la funzione è positiva negli intervalli: $ ( -oo ; -1 ) uu ( 0 ; +oo )$.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a $+oo$:
$ lim_(x to +oo) (x^2 + x) e^(x+1) $
Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:
$ lim_(x to +oo) (x^2 + x) e^(x+1) = +oo $
Calcoliamo ora il limite a $-oo$ :
$ lim_(x to -oo) (x^2 + x) e^(x+1) $
In questo caso abbiamo una forma di indecisione del tipo $ oo * 0 $; per risolverla, possiamo portare l’esponenziale al denominatore:
$ lim_(x to -oo) (x^2 + x) e^(x+1) = lim_(x to -oo) frac( x^2 + x)(e^(-x-1)) $
Ora sia numeratore che denominatore tendono a $+oo$, ma il denominatore è un infinito di ordine maggiore del numeratore, quindi tenderà ad infinito più velocemente; il valore del limite è quindi:
$ lim_(x to -oo) frac( x^2 + x)(e^(-x-1)) = 0 $
La retta $ y = 0$ è quindi un asintoto orizzontale sinistro per la funzione.
Poiché non ci sono asintoti orizzontali per $x to +oo$, occorre verificare se la funzione presenta asintoti obliqui per $x to +oo$:
$ m = lim_(x to oo) frac(f(x))(x) = lim_(x to oo) frac( x + 1)(e^(x+1)) = +oo $
Abbiamo trovato un valore infinito del limite, di conseguenza non sono presenti asintoti obliqui.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = (2x + 1) e^(x+1) + (x^2 + x) e^(x+1) = $
$ e^(x+1) (2x + 1 + x^2 + x) = $
$ e^(x+1) (x^2 + 3x + 1) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to e^(x+1) (x^2 + 3x + 1) = 0 $
$ x^2 + 3x + 1 = 0 to x = frac(-3 + sqrt5)(2) uu x = frac(-3 – sqrt5)(2) $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to e^(x+1) (x^2 + 3x + 1) > 0 $
$ e^(x+1) > 0 $
$ x^2 + 3x + 1 > 0 $
Dallo studio del segno si ottengono i seguenti intervallo:
$ ( – oo , frac(-3 – sqrt5)(2) ) uu ( frac(-3 + sqrt5)(2) ; +oo) $;
la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che il punto individuato da $ x = frac(-3 + sqrt5)(2) $ è un punto di minimo relativo per la funzione, mentre il punto individuato da $ x = frac(-3 – sqrt5)(2) $ è un punto di massimo relativo per la funzione.
Calcoliamo ora la derivata seconda della funzione:
$ f’’(x) = e^(x+1) (x^2 + 3x + 1) + e^(x+1) (2x + 3) = $
$e^(x+1) (x^2 + 3x + 1 + 2x + 3) = $
$ e^(x+1) (x^2 + 5x + 4) $
Troviamo i valori di x che annullano la derivata seconda:
$ f’’(x) = 0 to e^(x+1) (x^2 + 5x + 4) = 0 $
$ x^2 + 5x + 4 = 0 to x = frac(-5 pm sqrt(25 – 16))(2) = frac(-5 pm 3)(2) $
$ x = -1 uu x = -4 $
Studiamo il segno della derivata seconda:
$ f’’(x) > 0 to e^(x+1) (x^2 + 5x + 4) > 0$
$ e^(x+1) > 0 $
$ x^2 + 5x + 4 > 0 $
Dallo studio del segno si trova che $ x < -4 uu x > -1 $ ; di conseguenza, la funzione sarà concava verso l’alto per x in tale intervallo, e sarà rivolta verso il basso per $ -4 < x < -1$. I punti individuati da $ x = -4$ e $ x = -1$ sono quindi punti di flesso.
Possiamo tracciare il grafico della funzione:
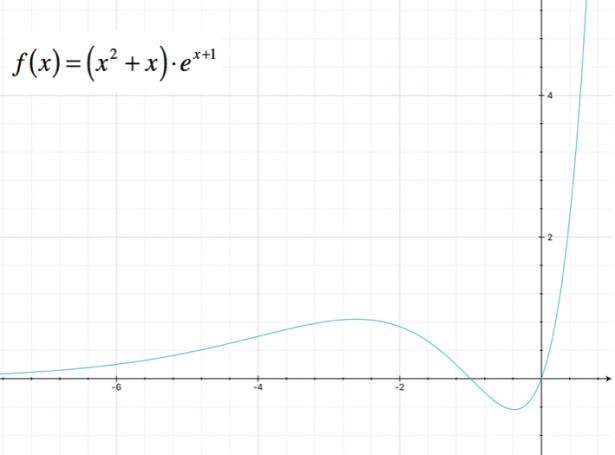
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
- Funzioni pari, dispari, crescenti e decrescenti (videolezione)
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = frac(1)(sinx) + frac(1)(cosx) $
La funzione in questione è una funzione trigonometrica fratta, quindi dobbiamo escludere dal dominio i valori di x che annullano i denominatori:
$ sin(x) = 0 to x = kπ , k in Z $
$ cos(x) = 0 to x = π/2 + kπ , k in Z $
Quindi, il dominio della funzione é $ D = R – { kπ ; π/2 + kπ} , k in Z $.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ (x = 0) $
La funzione non presenta punti di intersezione con l’asse y, in quanto il valore $x = 0$ è escluso dal dominio.
$ f(x) _|_ (y = 0) $
$ f(x) = 0 to frac(1)(sinx) + frac(1)(cosx) = 0 $
$ frac(1)(sinx) = – frac(1)(cosx) to cos(x) = – sin(x) $
$ x = -π/4 + 2kπ V x = 3/4 π + 2kπ to x = -π/4 + kπ $
Otteniamo i punti $ ( x = -π/4 + 2kπ ; 0 ) $.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = frac(1)(sin(-x)) + frac(1)(cos(-x)) = frac(1)(- sin(x)) + frac(1)(cos(x)) $
La funzione quindi non è ne pari ne dispari.
Cerchiamo i punti in cui la funzione è positiva:
$ f(x) > 0 to frac(1)(sin(x)) + frac(1)(cos(x)) > 0$
$ frac(cos(x) + sin(x))(sin(x) cos(x)) > 0 $
$ cos(x) + sin(x) > 0 to -π/4 + 2kπ < x < 3/4 π + 2kπ $ $sin(x) cos(x) > 0 to 0 + kπ < x < π/2 + kπ $
Dallo studio del segno si ottengono i seguenti intervalli:
$ 2kπ < x < π/2 uu 3/4 π + 2kπ < x < π + 2kπ uu $
$ uu 3/2π + 2kπ < x < 7/4π + 2kπ $
In tali intervalli la funzione è crescente.
Passiamo ora alla ricerca degli asintoti; dobbiamo quindi determinare i limiti della funzione. In questo caso, essendo lai funzione periodica, non ha senso calcolare i limiti a $pm oo$. Dato che la funzione non è definita in $ x = kπ$ e $ x = π/2 + kπ$, calcoliamo i limiti per x che tende a tali punti, che potrebbero rappresentare degli asintoti verticali:
$ lim_(x to kπ) frac(1)(sinx) + frac(1)(cosx) = oo $
Quindi le rette di equazione $ x = kπ$ rappresentano asintoti verticali per la funzione; allo stesso modo:
$ lim_(x to π/2 + kπ) frac(1)(sinx) + frac(1)(cosx) = oo $
Quindi anche le rette di equazione $ x = π/2 + kπ$ rappresentano asintoti verticali per la funzione.
Studiamo ora il comportamento della derivata prima della funzione: $ f’(x) = – frac(cosx)(sin^2(x)) + frac(sin(x))(cos^2(x)) = frac(sin^3(x) – cos^3(x))( sin^2(x) cos^2(x)) $
Troviamo i punti in cui la deriva prima si annulla:
$ f’(x) = 0 to frac(sin^3(x) – cos^3(x))( sin^2(x) cos^2(x)) = 0 $
$ sin^3(x) – cos^3(x) = 0 to sin^3(x) = cos^3(x) $
$ sin(x) = cos(x) to x = π/4 + kπ $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to frac(sin^3(x) – cos^3(x))( sin^2(x) cos^2(x)) > 0 $
$ sin^3(x) – cos^3(x) > 0 $
$ sin^2(x) cos^2(x) > 0 $
Dallo studio del segno si ottengono i seguenti intervallo:
$ ( π/4 + 2kπ , 5/4 π + 2kπ ) $
ciò significa che la funzione è crescente in tali intervalli. Di conseguenza, possiamo affermare che in corrispondenza dei punti $ x = π/4 + 2kπ $ la funzione presente dei minimi relativi, mentre in corrispondenza dei punti $ x = 5/4π + 2kπ $ la funzione presente dei massimi relativi.
Possiamo procedere rappresentando il grafico approssimativo della funzione:
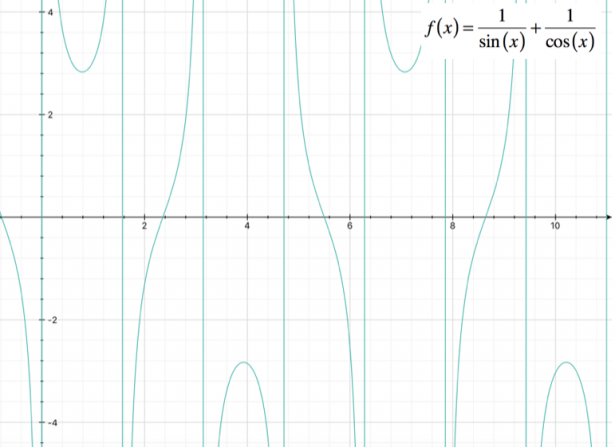
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = x * e^(frac(x)(1 + x)) $
La funzione esponenziale di per se è definita in tutto $R$; in questo caso, però, l’esponente è una frazione, quindi, dobbiamo escludere dal dominio i valori che annullano il denominatore; in questo caso:
$ 1 + x = 0 to x = -1 $
Quindi il dominio sarà l’insieme dei numeri reali eccetto il numero -1:
$ D = R – {-1} $.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) int x = 0$
$ f(0) = 0 * e^(frac(0)(1 + 0)) =0 $
Il punto individuato è $ ( 0 ; 0 ) $.
$ f(x) _!_ (y = 0)$
$ f(x) = 0 to x * e^(frac(x)(1 + x)) = 0 to x = 0$
In entrambi i casi otteniamo come punto di intersezione l’origine degli assi.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = – x * e^(frac(-x)(1 – x)) $
La funzione quindi non è ne pari ne dispari.
Cerchiamo gli intervalli in cui la funzione è positiva:
$ f(x) > 0 to x * e^(frac(x)(1 + x)) > 0 to x > 0 $
Poiché l’esponenziale è sempre positiva, la funzione è positiva nell’intervallo: $ ( 0 ; +oo ) $.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a $+oo$:
$ lim_(x to +oo) x * e^(frac(x)(1 + x)) $
Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:
$ lim_(x to +oo) x * e^(frac(x)(1 + x)) = +oo $
Analogamente, il limite a $-oo$ sarà:
$ lim_(x to -oo) x * e^(frac(x)(1 + x)) = -oo $
La funzione, quindi, non ha asintoti orizzontali; in questo caso possiamo passare alla ricerca degli asintoti obliqui:
$ m = lim_(x to oo) frac(f(x))(x) = lim_(x to oo) e^(frac(x)(1 + x)) = e $
Abbiamo trovato un valore finito del limite, che rappresenta il valore del coefficiente angolare dell’eventuale asintoto; proseguiamo con il calcolo dell’intercetta:
$ q = lim_(x to oo) [ f(x) – mx] = lim_(x to oo) [ x * e^(frac(x)(1 + x)) – ex] = $
$ lim_(x to oo) [ x * (e^(frac(x)(1 + x)) – e) ] = lim_(x to oo) [ ex * (e^(-frac(1)(1 + x)) – 1) ] $
Cerchiamo di ricondurre il limite ad un limite notevole:
$ lim_(x to oo) [ frac(-ex)(x+1) * frac((e^(-frac(1)(1 + x)) – 1))(-frac(1)(x+1)) ] = -e $
Possiamo quindi determinare l’equazione dell’asintoto obliquo:
$ y = ex – e $
Poiché la funzione non è definita in $x = -1$, verifichiamo se in tale punto è presente un asintoto verticale calcolando i seguenti limiti:
$ lim_(x to -1^+) x * e^(frac(x)(1 + x)) , lim_(x to -1^-) x * e^(frac(x)(1 + x)) $
I limiti destro e sinistro assumono i seguenti valori:
$ lim_(x to -1^+) x * e^(frac(x)(1 + x)) = 0 $
$ lim_(x to -1^-) x * e^(frac(x)(1 + x)) = – oo $
Quindi, la retta $ x = – 1$ è asintoto verticale (sinistro) per la funzione; “da destra” la funzione si avvicina a tale punto, senza mai raggiungerlo.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = e^(frac(x)(1+x)) + x * e^(frac(x)(1+x)) * frac(1+x-x)((1+x)^2) =$
$ e^(frac(x)(1+x)) * ( 1 + frac(x)((x+1)^2) ) = e^(frac(x)(1+x)) * frac(x^2 + 3x + 1)((x+1)^2) $
Troviamo i punti in cui la derivata prima si annulla:
$ f’(x) = 0 to e^(frac(x)(1+x)) * frac(x^2 + 3x + 1)((x+1)^2) = 0 $
$ x^2 + 3x + 1 = 0 to $
$ x = frac(-3 + sqrt5)(2) vee x = frac(-3 – sqrt5)(2) $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to e^(frac(x)(1+x)) * frac(x^2 + 3x + 1)((x+1)^2) > 0 $
$ e^(frac(x)(1+x)) > 0 $
$ x^2 + 3x + 1 > 0 $
$ (x+1)^2 > 0 $
Dallo studio del segno si ottengono i seguenti intervallo: $ ( – oo , frac(-3 – sqrt5)(2) ) uu ( frac(-3 + sqrt5)(2) ; +oo) $; la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che il punto individuato da $ x = frac(-3 + sqrt5)(2) $ è un punto di minimo relativo per la funzione, mentre il punto individuato da $ x = frac(-3 – sqrt5)(2) $ è un punto di massimo relativo per la funzione.
In questo caso, lo studio della derivata seconda si rileva troppo complesso; possiamo comunque procedere rappresentando il grafico approssimativo della funzione:
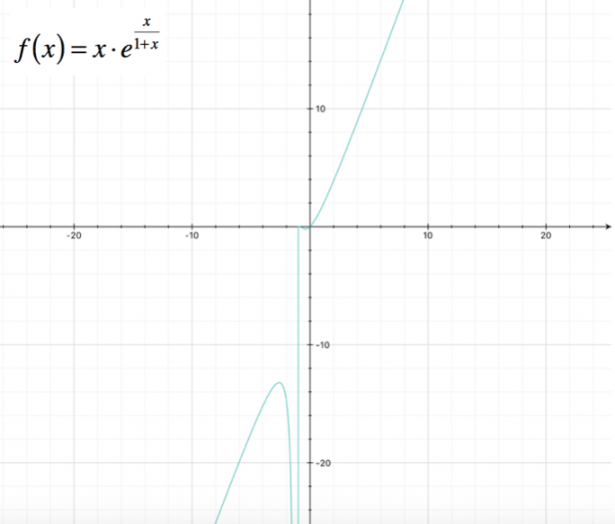
In dettaglio mostriamo l’andamento della funzione nell’intervallo $(-1 ; 0)$ :
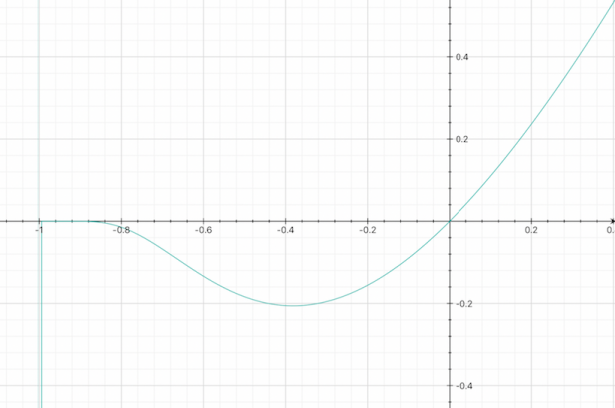
Io penso che tu creda che lei sappia
«Io penso che tu creda che lei sappia» è il titolo dell’ultimo libro pubblicato dalla Sironi Editore per la collana Galapagos. L’autore Bruno Codenotti, direttore di ricerca presso l’Istituto di Informatica e Telematica del CNR di Pisa, si era già dedicato alla divulgazione con «Un biglietto di sola andata», mentre con il successivo «Archimede aveva un sacco di tempo libero» ha avviato la collaborazione, portata avanti anche in questo testo, con Claudia Flandoli, illustratrice e fumettista. «Frutto di un prolungato confronto» tra gli autori, come ci viene specificato nella nota iniziale, il testo porta in sé la ricchezza delle esaurienti spiegazioni di Codenotti e la simpatica chiarezza dei fumetti della Flandoli. Continua a leggere “Io penso che tu creda che lei sappia”
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = frac(e^(-x^2))(x + 2) $
La funzione può essere scritta anche nel modo seguente:
$ f(x) = frac(1)( e^(x^2) (x + 2)) $
Nel caso di funzioni fratte, dobbiamo escludere dal dominio i valori che annullano il denominatore; in questo caso:
$ e^(x^2) (x + 2) = 0 to x + 2 = 0 to x = – 2$
Quindi il dominio sarà l’insieme dei numeri reali eccetto il numero -2:
$ D = R – {-2} $.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) _|_ (x = 0) $
$ f(0) = frac(1)( e^(0^2) (0 + 2)) =1/2 $
Il punto individuato è $ ( 0 ; 1/2 ) $.
Quindi la funzione ha un punto di intersezione con l’asse y.
$ f(x) _|_ y = 0$
$ f(x) = 0 to frac(1)( e^(x^2) (x + 2)) = 0 $
Dato che l’uguaglianza non può essere verificata per nessun valore di x, concludiamo che la funzione non presenta punti di intersezione con l’asse x.
Verifichiamo se la funzione è pari o dispari:
$ f(-x) = frac(1)( e^((-x)^2) (-x + 2)) = frac(1)( e^(x^2) (-x + 2)) $
La funzione quindi non è ne pari ne dispari.
Cerchiamo gli intervalli in cui la funzione è positiva:
$ f(x) > 0 to frac(1)( e^(x^2) (x + 2)) > 0 to e^(x^2) (x + 2) > 0 $
$ x + 2 > 0 to x > – 2 $
La funzione è positiva nel seguente intervallo: $ ( -2 ; +oo ) $.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a $oo$:
$ lim_(x to oo) frac(1)( e^(x^2) (x + 2)) $
Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:
$ lim_(x to oo) frac(1)( e^(x^2) (x + 2)) = 0 $
La funzione, quindi, ha come asintoto orizzontale (destro e sinistro) la retta di equazione $y = 0$ .
Poiché la funzione non è definita in $x = -2$, verifichiamo se in tale punto è presente un asintoto verticale calcolando i seguenti limiti:
$ lim_(x to -2^+) frac(1)( e^(x^2) (x + 2)) , lim_(x to -2^-) frac(1)( e^(x^2) (x + 2)) $
I limiti destro e sinistro assumono i seguenti valori:
$ lim_(x to -2^+) frac(1)( e^(x^2) (x + 2)) = + oo $
$ lim_(x to -2^-) frac(1)( e^(x^2) (x + 2)) = – oo $
Quindi, la retta $ x = – 2$ è asintoto verticale (destro e sinistro) per la funzione.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = – frac(e^(x^2) * 2x(x + 2) + e^(x^2) )( e^(2x^2)(x+2)^2 ) = – frac( 2x^2 + 4x + 1)( e^(x^2)(x+2)^2 ) $
Troviamo i punti in cui la derivata prima si annulla:
$ f’(x) = 0 to – frac( 2x^2 + 4x + 1)( e^(x^2)(x+2)^2 ) = 0 $
$ 2x^2 + 4x + 1 = 0 to x = -1 + frac(sqrt2)(2) V x = -1 – frac(sqrt2)(2) $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to – frac( 2x^2 + 4x + 1)( e^(x^2)(x+2)^2 ) > 0 $
$ – (2x^2 + 4x + 1) > 0 $
$ e^(x^2) > 0 $
$ (x+2)^2 > 0 $
Dallo studio del segno si ottiene l’intervallo: $ ( -1 – frac(sqrt2)(2) , -1 + frac(sqrt2)(2) ) $; la funzione, quindi, è crescente in tale intervallo.
Notiamo, quindi, che il punto individuato da $ x = -1 – frac(sqrt2)(2) $ è un punto di minimo relativo per la funzione, mentre il punto individuato da $ x = -1 + frac(sqrt2)(2) $ è un punto di massimo relativo per la funzione
In questo caso, lo studio della derivata seconda si rileva troppo complesso; possiamo comunque procedere rappresentando il grafico approssimativo della funzione:
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
Studiare la seguente funzione, determinandone il dominio, i punti di intersezione con gli assi, eventuali punti di massimo e minimo, e punti di flesso; verificare la presenza di asintoti, e tracciare il grafico approssimativo. $ f(x) = frac(2x^2 – 1)(x^2 + 1) $
Nel caso di funzioni fratte, nella determinazione del dominio si deve tener conto degli eventuali punti in cui la funzione potrebbe non essere definita, e questi sono i punti per cui il denominatore della funzione si annulla; in questo caso abbiamo:
$ D = 0 to x^2 + 1 = 0 to x^2 = – 1$
Poiché il denominatore è una quantità sempre diversa da zero, possiamo concludere che il dominio della funzione è tutto $R$.
Determiniamo ora i punti di intersezione con gli assi:
$ f(x) int x = 0$
$ f(0) = frac(2 * 0^2 – 1)(0^2 + 1) = – 1$
Il punto individuato è $ (0 ; -1) $.
$ f(x) int y = 0$
$ f(x) = 0 to frac(2 x^2 – 1)(x^2 + 1) = 0 to x = pm frac(sqrt2)(2) $
I punti individuati sono $ ( frac(sqrt2)(2) ; 0 ) $ e $ ( – frac(sqrt2)(2) ; 0 ) $.
Quindi la funzione ha un punto di intersezione con l’asse y e due punti di intersezione con l’asse x.
Notiamo che $ f(x) = f(-x)$, quindi la funzione è pari, ovvero simmetrica rispetto all’asse y.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, in questo caso, a $+oo$ e $-oo$:
$ lim_(x to oo) frac(2 x^2 – 1)(x^2 + 1) $
Poiché numeratore e denominatore sono dello stesso grado, il limite vale $2$; tale limite vale sia per $+oo$ che per $-oo$.
Abbiamo, quindi, la presenza di un asintoto orizzontale; dato che il valore del limite è 2, l’equazione dell’asintoto orizzontale è $ y = 2$.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
$ f’(x) = frac(4x(x^2 + 1) – (2x^2 – 1)*2x )( (x^2 + 1)^2 ) = frac(6x)( (x^2 + 1)^2 ) $
Troviamo i punti in cui la derivata prima si annulla:
$ f’(x) = 0 to frac(6x)( (x^2 + 1)^2 ) = 0 to x = 0 $
Studiamo il segno della derivata prima:
$ f’(x) > 0 to frac(6x)( (x^2 + 1)^2 ) > 0 to x > 0 $
Dallo studio della derivata prima possiamo capire che la funzione sarà crescente per $x>0$, quindi necessariamente essa presenterà un punto di minimo in $0$; tale punto di minimo corrisponde al punto di intersezione con l’asse y determinato in precedenza.
Passiamo allo studio della derivata seconda:
$ f’’(x) = frac( 6(x^2 + 1)^2 – 6x * 2(x^2 + 1)*2x )( (x^2 + 1)^4 ) = frac(6x^2 + 6 – 24x^2)( (x^2 + 1)^3 ) = frac(6 – 18 x^2)((x^2 + 1)^3) $
Troviamo i punti in cui la deriva seconda si annulla:
$ f’’(x) = 0 to frac(6 – 18 x^2)((x^2 + 1)^3) = 0 to x = pm frac(sqrt3)(3) $
Studiamo il segno della derivata seconda:
$ f’’(x) > 0 to frac(6 – 18 x^2)((x^2 + 1)^3) > 0 $
$ 6 – 18 x^2 > 0 to – frac(sqrt3)(3) < x < frac(sqrt3)(3) $
La funzione, quindi, presenta una concavità verso l’alto nell’intervallo $- frac(sqrt3)(3) < x < frac(sqrt3)(3) $; in particolare, si ha che:
$ f(frac(sqrt3)(3)) = f(-frac(sqrt3)(3)) = frac(2/3 – 1)(1/3 + 1) = – 1/4 $
di conseguenza, i punti $ ( frac(sqrt3)(3) ; – 1/4 ) $ e $ ( – frac(sqrt3)(3) ; – 1/4 ) $ sono punti di flesso.
Possiamo quindi procedere rappresentando il grafico della funzione:
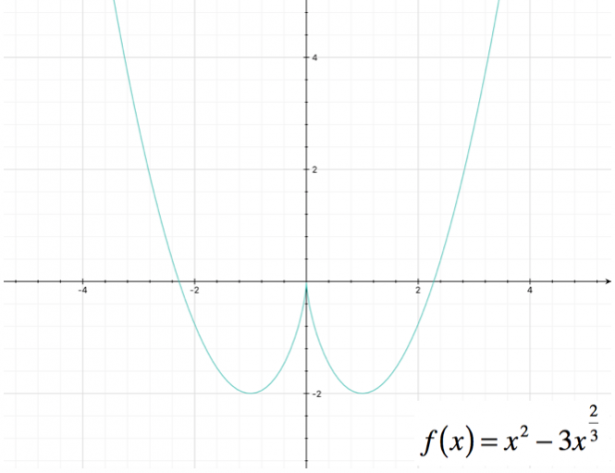
Potrebbe interessarti anche
- Appunti sullo Studio di funzioni
Calcolare il valore del seguente limite: $ lim_(x to 0) frac( e^(x^2) – 1 – x log(1 + x) )( tg^2(x) * log(1+x) ) $
Per risolvere questo limite risulta complicato procede con metodi “tradizionali”, in quanto è difficile potersi ricondurre a limiti notevoli, o applicare proprietà note; il limite, infatti, si presenta nella forma indeterminata $0/0$.
In questi casi, poiché il limite è per $ x to 0$, è utile procedere sviluppando numeratore e denominatore in serie di Taylor.
Cominciamo dal numeratore; ricordiamo che:
$ log(1+x) = x – frac(x^2)(2) + frac(x^3)(3) – …. + frac((-1)^(n+1))(n) x^n + o(x^n) $ per $ |x| < 1 $
$ e^x = 1 + x + frac(x^2)(2) + ….. + frac(x^n)(n!) + o(x^n) $
Nel nostro caso, quindi, sviluppando al terzo ordine otteniamo:
$ N = 1 + x^2 + frac( (x^2)^2)(2) + o((x^2)^2) – 1 – x(x – frac(x^2)(2) + frac(x^3)(3) + o(x^3)) = $
$ 1 + x^2 + frac(x^4)(2) + o(x^4) – 1 – x^2 + frac(x^3)(2) – frac(x^4)(3) + o(x^4) = $
$ frac(x^3)(2) – frac(x^4)(6) + o(x^4) $
Sviluppiamo anche il denominatore; per determinare lo sviluppo della funzione tangente ricordiamo che:
$ f(x) = f(x_0) + frac(f^(1)(x_0))(1!) (x – x_0) + frac(f^(2)(x_0))(2!) (x – x_0)^2 + … $
Se chiamiamo $ g(x) = tg(x) $, abbiamo che:
$ g(0) = 0$
$ g’(x) = frac(1)(cos^2(x)) $
e $ g’(0) = 1$ ; quindi, al primo ordine la funzione sarà:
$ g(x) = x + o(x) $
Proviamo a fermarci al primo ordine, e a sviluppare la funzione $ log(x+1) $ al secondo ordine; l’obiettivo è quello di ottenere funzioni di grado terzo al denominatore.
Al denominatore avremmo quindi:
$ D = (x + o(x))^2 ( x – frac(x^2)(2) + o(x^2) ) = (x^2 + o(x^2)) ( x – frac(x^2)(2) + o(x^2) ) = $
$ x^3 – frac(x^4)(2) + o(x^4) $
Tornando al limite si ottiene:
$ lim_(x to 0) frac( frac(x^3)(2) – frac(x^4)(6) + o(x^4) )( x^3 – frac(x^4)(2) + o(x^4)) $
A questo punto numeratore e denominatore sono confrontabili, in quanto presentano entrambi le funzioni di grado minore dello stesso grado. Possiamo, quindi, pensare di mettere in evidenza al numeratore e al denominatore il fattore $x^3$, e di semplificarlo:
$ lim_(x to 0) frac( frac(1)(2) – frac(x)(6) + o(x) )( 1 – frac(x)(2) + o(x)) $
A questo punto siamo in grado di calcolare il limite:
$ lim_(x to 0) frac( frac(1)(2) – frac(x)(6) + o(x) )( 1 – frac(x)(2) + o(x)) = 1/2 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(x to 0) frac( log(1 + x^3) – sin^3(x) )( x^2 arctg(x^3) ) $
Per risolvere questo limite risulta complicato procede con metodi “tradizionali”, in quanto è difficile potersi ricondurre a limiti notevoli, o applicare proprietà note; il limite, infatti, si presenta nella forma indeterminata $0/0$.
In questi casi, poiché il limite è per $ x to 0$, è utile procedere sviluppando numeratore e denominatore in serie di Taylor.
Cominciamo dal numeratore; ricordiamo che:
$ log(1+x) = x – frac(x^2)(2) + frac(x^3)(3) – …. + frac((-1)^(n+1))(n) x^n + o(x^n) $ per $ |x| < 1 $
$ sin(x) = x – frac(x^3)(6) + ….. + frac((-1)^n x^(2n+1))((2n+1)!) + o(x^(2n+1)) $
Nel nostro caso, quindi, sviluppando al secondo ordine otteniamo:
$ N = x^3 – frac((x^3)^2)(2) + o((x^3)^2) – (x – frac(x^3)(6) + o(x^3))^3 = $
$ x^3 – frac(x^6)(2) + o(x^6) – x^3 + frac(x^5)(2) + o(x^5) = $
$ frac(x^5)(2) + o(x^5) $
Sviluppiamo anche il denominatore, questa volta dobbiamo sviluppare la funzione arcotangente al primo ordine in modo da ottenere terze potenze (l’argomento della funzione, infatti, è già elevato alla terza);in questo modo, dato che la funzione è moltiplicata per $x^2$, otterremo comunque un quinto grado al denominatore.
Lo sviluppo della funzione arcotangente può essere determinato calcolando le derivate della funzione, sapendo che in generale:
$ f(x) = f(x_0) + frac(f^(1)(x_0))(1!) (x – x_0) + frac(f^(2)(x_0))(2!) (x – x_0)^2 + … $
Se chiamiamo $ g(x) = arctg(x) $, abbiamo che:
$ g(0) = 0$
$ g’(x) = frac(1)(1 + x^2)) $
e $ g’(0) = 1$ ; quindi, al primo ordine la funzione sarà:
$ g(x) = x + o(x) $
$ g’’(x) = frac(2x)(2sqrt(1 – x^2) * (1-x^2)) $
Al denominatore avremmo quindi:
$ D = x^2 ( x^3 + o(x^3) ) = x^5 + o(x^5) $
Tornando al limite si ottiene:
$ lim_(x to 0) frac( frac(x^5)(2) + o(x^5) )( x^5 + o(x^5) ) $
Essendo numeratore e denominatore dello stesso grado, possiamo pensare di “semplificare” i termini $x^5$, ottenendo quindi:
$ lim_(x to 0) frac( frac(1)(2) + o(1) )( 1 + o(1) ) = 1/2 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(x to 0) frac( sin^2(x) – log(1 + x^2) )( x^2 – x arcsin(x) ) $
Per risolvere questo limite risulta complicato procede con metodi “tradizionali”, in quanto è difficile potersi ricondurre a limiti notevoli, o applicare proprietà note; il limite, infatti, si presenta nella forma indeterminata $0/0$.
In questi casi, poiché il limite è per $ x to 0$, è utile procedere sviluppando numeratore e denominatore in serie di Taylor.
Cominciamo dal numeratore; ricordiamo che:
$ log(1+x) = x – frac(x^2)(2) + frac(x^3)(3) – …. + frac((-1)^(n+1))(n) x^n + o(x^n) per |x| < 1 $
$ sin(x) = x – frac(x^3)(6) + ….. + frac((-1)^n x^(2n+1))((2n+1)!) + o(x^(2n+1)) $
Nel nostro caso, quindi, sviluppando al secondo ordine otteniamo:
$ N = (x – 1/6 x^3 + o(x^3))^2 – (x^2 – frac(x^4)(2) + o(x^4)) = $
$ x^2 – 1/3 x^4 – x^2 + frac(x^4)(2) + o(x^4) = frac(x^4)(6) + o(x^4) $
Nei calcoli precedenti, le potenze di ordine superiore al quarto sono state ignorate, in quanto “inglobate” all’interno di $ o(x^4)$.
Sviluppiamo anche il denominatore, questa volta dobbiamo sviluppare la funzione arcoseno al terzo ordine in modo da ottenere terze potenze; dato che la funzione è moltiplicata per $x$, otterremo comunque un quarto grado al denominatore.
Lo sviluppo della funzione arcoseno può essere determinato calcolando le derivate della funzione, sapendo che in generale:
$ f(x) = f(x_0) + frac(f^(1)(x_0))(1!) (x – x_0) + frac(f^(2)(x_0))(2!) (x – x_0)^2 + …$
Se chiamiamo $ g(x) = arcsin(x) $, abbiamo che:
$ g’(x) = frac(1)(sqrt(1 – x^2)) $
e $ g’(0) = 1$ ; quindi, al primo ordine la funzione sarà:
$ g(x) = x + o(x) $
$ g’’(x) = frac(2x)(2sqrt(1 – x^2) * (1-x^2)) $
e $ g’’(0) = 0$ ; proseguiamo, quindi, calcolando la derivata terza:
$ g’’’(x) = frac(1 + 3x – x^2)(sqrt(1 – x^2) * (1-x^2)^2) $
$ g’’’(0) = 1$ ; quindi, al terzo ordine la funzione sarà:
$ g(x) = x + 1/6 x^3 + o(x^3) $
Al denominatore avremmo quindi:
$ D = x^2 – x( x + 1/6 x^3 + o(x^3) ) = x^2 – x^2 – 1/6 x^4 + o(x^4) = $
$ -1/6 x^4 + o(x^4) $
Tornando al limite si ottiene:
$ lim_(x to 0) frac( frac(x^4)(6) + o(x^4) )( -1/6 x^4 + o(x^4) ) $
Essendo numeratore e denominatore dello stesso grado, possiamo pensare di “semplificare” i termini $x^4$, ottenendo quindi:
$ lim_(x to 0) frac( frac(1)(6) + o(1))( -1/6 + o(1)) = -1 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(x to 0) frac( cos(sqrt2 x^2) – e^(-x^4) )( x^5 * (arcsin(x))^3) $
Per risolvere questo limite risulta complicato procede con metodi “tradizionali”, in quanto è difficile potersi ricondurre a limiti notevoli, o applicare proprietà note; il limite, infatti, si presenta nella forma indeterminata $0/0$.
In questi casi, poiché il limite è per $ x to 0$, è utile procedere sviluppando numeratore e denominatore in serie di Taylor.
Cominciamo dal numeratore; ricordiamo che:
$ e^x = 1 + x + frac(x^2)(2) + ….. + frac(x^n)(n!) + o(x^n) $
$ cos(x) = 1 – frac(x^2)(2) + ….. + frac((-1)^n x^(2n))((2n)!) + o(x^(2n)) $
Nel nostro caso, quindi, sviluppando al secondo ordine otteniamo:
$ N = 1 – frac( (sqrt2 x^2)^2 )(2) + frac((sqrt2 x^2)^4)(4!) – 1 + x^4 – frac(x^8)(2) + o(x^8) = $
$ frac(x^8)(6) – frac(x^8)(2) + o(x^8) = – frac(x^8)(3) + o(x^8) $
Sviluppiamo anche il denominatore, questa volta dobbiamo sviluppare la funzione arcoseno al primo ordine in modo da ottenere terze potenze, in quanto la funzione è elevata alla terza e moltiplicata poi per un fattore $x^5$, e questo ci permette comunque di ottenere un infinitesimo di ordine 8 anche al denominatore.
Lo sviluppo della funzione arcoseno può essere determinato calcolando le derivate della funzione, sapendo che in generale:
$ f(x) = f(x_0) + frac(f^(1)(x_0))(1!) (x – x_0) + frac(f^(2)(x_0))(2!) (x – x_0)^2 + ….
Se chiamiamo $ g(x) = arcsin(x) $, abbiamo che:
$ g’(x) = frac(1)(sqrt(1 – x^2)) $
e $ g’(0) = 1$ ; quindi, al primo ordine la funzione sarà:
$ g(x) = x + o(x) $
Al denominatore avremmo quindi:
$ D = x^5 ( x + o(x) )^3 $
Applicando le proprietà algebriche dell’o-piccolo, abbiamo che:
$ D = x^5 ( x + o(x) )^3 = x^5 ( x^3 + o(x^3)) = x^8 + o(x^8) $
Possiamo quindi fermarci qui; tornando al limite si ottiene:
$ lim_(x to 0) frac( – frac(x^8)(3) + o(x^8) )( x^8 + o(x^8) ) $
Essendo numeratore e denominatore dello stesso grado, possiamo pensare di “semplificare” i termini $x^4$, ottenendo quindi:
$ lim_(x to 0) frac( -frac(1)(3) + o(1))( 1 + o(1)) = -1/3 $
Potrebbe interessarti anche
- Appunti sui Limiti
- Appunti di Goniometria
Calcolare il valore del seguente limite: $ lim_(x to 0) frac(e^(-x^2) – cos(sqrt2 x))( x^3 * sin(x)) $
Per risolvere questo limite risulta complicato procede con metodi “tradizionali”, in quanto è difficile potersi ricondurre a limiti notevoli, o applicare proprietà note; il limite, infatti, si presenta nella forma indeterminata $0/0$.
In questi casi, poiché il limite è per $ x to 0$, è utile procedere sviluppando numeratore e denominatore in serie di Taylor.
Cominciamo dal numeratore; ricordiamo che:
$ e^x = 1 + x + frac(x^2)(2) + ….. + frac(x^n)(n!) + o(x^n) $
$ cos(x) = 1 – frac(x^2)(2) + ….. + frac((-1)^n x^(2n))((2n)!) + o(x^(2n)) $
Nel nostro caso, quindi, sviluppando al secondo ordine otteniamo:
$ N = 1 + (-x^2) + frac((-x^2)^2)(2) + o(x^4) – ( 1 – frac((sqrt2 x)^2)(2) + frac((sqrt2 x)^4)(4!) + o(x^4) ) = $
$ 1 – x^2 + frac(x^4)(4) -1 + x^2 – frac(x^4)(6) + o(x^4) = $
$ frac(x^4)(3) + o(x^4) $
Sviluppiamo anche il denominatore, questa volta ci possiamo fermare al primo ordine, in quanto il seno è moltiplicato per un fattore $x^3$, e questo ci permette comunque di ottenere un infinitesimo di ordine 4 anche al denominatore.
Ricordiamo che lo sviluppo della funzione seno è il seguente:
$ sin(x) = x – frac(x^3)(6) + ….. + frac((-1)^n x^(2n+1))((2n+1)!) + o(x^(2n+1)) $
Abbiamo quindi:
$ D = x^3( x + o(x) ) = x^4 + o(x^4) $
Tornando al limite si ottiene:
$ lim_(x to 0) frac(frac(x^4)(3) + o(x^4))( x^4 + o(x^4)) $
Essendo numeratore e denominatore dello stesso grado, possiamo pensare di “semplificare” i termini $x^4$, ottenendo quindi:
$ lim_(x to 0) frac(frac(1)(3) + o(1))( 1 + o(1)) = 1/3 $
Potrebbe interessarti anche
- Appunti sui Limiti
Verificare, applicando la definizione, che vale il seguente limite: $ lim_(n to oo) sqrt(n^2 + n + 1) = + oo $
Nella dimostrazione di tale limite, teniamo presente che il limite è un limite infinito, cioè che la successione al crescere di $n$ tende ad un valore infinito (positivo); e che il parametro tende ad un valore infinito $ n to oo$.
La definizione, in questo caso, è la seguente:
$ forall M > 0, exists \bar{n} in N : forall n >= \bar{n} $
$ sqrt(n^2 + n + 1) > M $
Ovvero, dobbiamo dimostrare che, comunque scelto un $M$ molto grande (in modulo), esisterà un valore di $n$ per cui il valore della successione è più grande di $M$.
La verifica del limite consiste nel trovare (se esiste) un valore di $\bar{n} $ che soddisfi la disuguaglianza precedente.
Cominciamo, quindi, svolgendo la disuguaglianza:
$ sqrt(n^2 + n + 1) > M $
Eleviamo tutto al quadrato:
$ (sqrt(n^2 + n + 1))^2 > M^2 $
$ n^2 + n + 1 > M^2 $
Portiamo tutto a primo membro:
$ n^2 + n + 1 – M^2 > 0 $
Passiamo all’equazione associata (in $n$):
$ n^2 + n + 1 – M^2 = 0 $
Troviamo le soluzioni con la formula di risoluzione delle equazioni di secondo grado:
$ n = frac( -1 pm sqrt( 1 – 4 + 4M^2) )(2) = frac( -1 pm sqrt(4M^2 – 3) )(2) $
Poiché la diseguaglianza è maggiore di zero, le soluzioni sono date dai valori esterni all’intervallo delle radici:
$ n < frac( -1 – sqrt(4M^2 – 3) )(2) vee n > frac( -1 + sqrt(4M^2 – 3) )(2) $
Dato che la disuguaglianza, per le condizioni iniziali, deve valere $forall n >= \bar{n} $, e tenendo conto del risultato ottenuto, possiamo scegliere come valore di $\bar{n} $ un qualunque valore tale che:
$ \bar{n} > frac( -1 + sqrt(4M^2 – 3) )(2) $.
Poiché abbiamo trovato valori possibili per $\bar{n} $, possiamo concludere che il limite è verificato.
Potrebbe interessarti anche
- Appunti sui Limiti
- Appunti su Successioni e serie
Verificare, applicando la definizione, che vale il seguente limite: $ lim_(n to oo) sqrt(n) – n = – oo $
Nella dimostrazione di tale limite, teniamo presente che il limite è un limite infinito, cioè che la successione al crescere di $n$ tende ad un valore infinito (negativo); e che il parametro tende ad un valore infinito $ n to oo$.
La definizione, in questo caso, è la seguente:
$ forall M > 0, exists \bar{n} in N : forall n >= \bar{n} $
$ sqrt(n) – n < – M $
Ovvero, dobbiamo dimostrare che, comunque scelto un $M$ molto grande (in modulo), esisterà un valore di $n$ per cui il valore della successione è più piccolo di $ – M$.
La verifica del limite consiste nel trovare (se esiste) un valore di $\bar{n} $ che soddisfi la disuguaglianza precedente.
Cominciamo, quindi, svolgendo la disuguaglianza:
$ sqrt(n) – n < – M $
Isoliamo il termine $sqrt(n)$:
$ sqrt(n) < n – M $
Eleviamo tutto al quadrato:
$ (sqrt(n))^2 < (n – M)^2 $
$ n < n^2 + M^2 – 2nM $
Portiamo tutto a primo membro e cambiamo il segno:
$ n – n^2 – M^2 + 2nM < 0 $
$ n^2 – n – 2nM + M^2 < 0 $
$ n^2 – n (1 + 2M) + M^2 < 0 $
Passiamo all’equazione associata (in $n$):
$ n^2 – n (1 + 2M) + M^2 = 0 $
Troviamo le soluzioni con la formula di risoluzione delle equazioni di secondo grado:
$ n = frac( (1 + 2M) pm sqrt( (1 + 2M)^2 – 4M^2) )(2) $
Svolgiamo i calcoli sotto radice:
$ n = frac( (1 + 2M) pm sqrt( 1 + 4M^2 + 4M – 4M^2) )(2) = $
$ frac( (1 + 2M) pm sqrt( 1 + 4M) )(2) $
Poiché la diseguaglianza è maggiore di zero, le soluzioni sono date dai valori esterni all’intervallo delle radici:
$ n < frac( (1 + 2M) – sqrt( 1 + 4M) )(2) wedge n > frac( (1 + 2M) + sqrt( 1 + 4M) )(2) $
Dato che la disuguaglianza, per le condizioni iniziali, deve valere per ogni $n >= \bar{n} $, e tenendo conto del risultato ottenuto, possiamo scegliere come valore di $\bar{n} $ un qualunque valore tale che:
$ \bar{n} > frac( (1 + 2M) + sqrt( 1 + 4M) )(2) $.
Poiché abbiamo trovato valori possibili per $\bar{n} $, possiamo concludere che il limite è verificato.
Potrebbe interessarti anche
- Appunti sui Limiti
- Appunti su Successioni e serie
Verificare, applicando la definizione, che vale il seguente limite: $ lim_(n to oo) log_2 (1/n) = – oo $
Nella dimostrazione di tale limite, teniamo presente che il limite è un limite infinito, cioè che la successione al crescere di $n$ tende ad un valore infinito (negativo); e che il parametro tende ad un valore infinito $ n to oo$.
La definizione, in questo caso, è la seguente:
$ forall M > 0, exists \bar{n} in N : forall n >= \bar{n} $ risulta verificata l’espressione
$ log_2 (1/n) < – M $
Ovvero, dobbiamo dimostrare che, comunque scelto un $M$ molto grande (in modulo), esisterà un valore di $n$ per cui il valore della successione è più piccolo di $ – M$.
La verifica del limite consiste nel trovare (se esiste) un valore di $\bar{n} $ che soddisfi la disuguaglianza precedente.
Cominciamo, quindi, svolgendo la disuguaglianza:
$ log_2 (1/n) < – M $
Passiamo all’esponenziale:
$ 1/n < 2^(- M) to n > 2^M $
Dato che la disuguaglianza, per le condizioni iniziali, deve valere $per ogni n >= \bar{n} $, e tenendo conto del risultato ottenuto, possiamo scegliere come valore di $\bar{n} $ un qualunque valore tale che $ \bar{n} > 2^M $.
Poiché abbiamo trovato valori possibili per $\bar{n} $, possiamo concludere che il limite è verificato.
Potrebbe interessarti anche
- Appunti sui Limiti
Verificare, applicando la definizione, che vale il seguente limite: $ lim_(n to oo) frac(n^2 + 1)(n + 1) = + oo $
Nella dimostrazione di tale limite, dobbiamo tener presente che il limite è un limite infinito, cioè che la successione al crescere di $n$ tende ad un valore infinito; e che il parametro tende ad un valore infinito $ n to oo$.
La definizione, in questo caso, è la seguente:
$ forall M > 0, exists \bar{n} in N : forall n >= \bar{n} $ risulta in corrispondenza
$ frac(n^2 + 1)(n + 1) > M $
Ovvero, dobbiamo dimostrare che, comunque scelto un $M$ molto grande, esisterà un valore di $n$ per cui il valore della successione è più grande di $M$.
La verifica del limite consiste nel trovare (se esiste) un valore di $\bar{n} $ che soddisfi la disuguaglianza precedente.
Cominciamo, quindi, svolgendo la disuguaglianza:
$ frac(n^2 + 1)(n + 1) > M $
Svolgiamo il minimo comune multiplo:
$ n^2 + 1> M(n + 1) $
$ n^2 + 1> Mn + M $
Portiamo tutto a primo membro:
$ n^2 + 1- Mn – M > 0 $
Troviamo le soluzioni della disequazione di secondo grado in $n$ associata:
$ n^2 – Mn + 1 – M = 0 $
Risolviamo con la formula di risoluzione delle equazioni di secondo grado:
$ n = frac(M pm sqrt(M^2 – 4(1 – M) ) )(2) = frac(M pm sqrt(M^2 – 4 + 4M ) )(2) $
Poiché la disequazione è maggiore di zero, le soluzioni sono date dai valori esterni all’intervallo delle radici:
$ n < frac(M – sqrt(M^2 – 4 + 4M ) )(2) V n > frac(M + sqrt(M^2 – 4 + 4M ) )(2) $
Dato che la disuguaglianza, per le condizioni della definizione, deve valere $per ogni n >= \bar{n} $, e tenendo conto del risultato ottenuto, possiamo scegliere come valore di $\bar{n} $ un qualunque valore tale che:
$ \bar{n} > frac(M + sqrt(M^2 – 4 + 4M ) )(2) $.
Poiché abbiamo trovato valori possibili per $\bar{n} $, possiamo concludere che il limite è verificato.
Potrebbe interessarti anche
- Appunti sui Limiti
- Appunti su Successioni e serie numeriche
Verificare, applicando la definizione, che vale il seguente limite: $ lim_(n to oo) frac(2n + 3)(n + 1) = 2 $
Nella dimostrazione di tale limite, dobbiamo tener presente che il limite è un limite finito, cioè che la successione al crescere di $n$ tende ad un valore finito; e che il parametro tende ad un valore infinito $ n to oo$.
La definizione, in questo caso, è la seguente:
\( \forall \epsilon \gt 0, \exists \bar{n}\in N : \forall n \ge \bar{n}\) risulta
$ | frac(2n + 3)(n + 1) – 2 | < epsilon $
Ovvero, dobbiamo dimostrare che, comunque scelto un $epsilon$ piccolo a piacere, esisterà un valore di $n$ per cui la “distanza” della funzione dal valore limite sarà più piccola di $epsilon$.
La verifica del limite consiste nel trovare (se esiste) un valore di $\bar{n} $ che soddisfi la disuguaglianza precedente.
Cominciamo, quindi, svolgendo la disuguaglianza:
$ | frac(2n + 3)(n + 1) – 2 | < epsilon $
Sommiamo i termini all’interno del modulo:
$ | frac(2n + 3 – 2n – 2)(n + 1)| < epsilon $
$ | frac(1)(n + 1)| < epsilon $
Come sappiamo, una disequazione in cui è presente un modulo minore di un valore positivo $epsilon$ può essere risolta considerando i valori interni all’intervallo $ (-epsilon ; epsilon) $:
$ – epsilon < frac(1)(n + 1) < epsilon $
In questo caso è necessario impostare un sistema per risolvere le due disequazioni:
$ frac(1)(n + 1) < epsilon $ $ frac(1)(n + 1) > – epsilon $
Dalla prima otteniamo:
$ 1 < epsilon (n + 1) to 1/epsilon < n + 1 to n > 1/epsilon – 1 $
Dalla seconda:
$ 1 > – epsilon (n + 1) to -1/epsilon < n + 1 to n > – 1/epsilon – 1 $
Dovendo mettere a sistema le soluzioni, troviamo che la disuguaglianza è verificata per $n > 1/epsilon – 1 $.
Dato che la disuguaglianza, per le condizioni della definizione, deve valere per ogni $n >= \bar{n} $, e tenendo conto del risultato ottenuto, possiamo scegliere come valore di $\bar{n} $ un qualunque valore tale che $ \bar{n} > 1/epsilon – 1 $.
Poiché abbiamo trovato valori possibili per $\bar{n} $, possiamo concludere che il limite è verificato.
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(x to +oo) ( 2x – sqrt(4x^2+x) ) $
Il limite si presenta in una forma indeterminata del tipo $ +oo -oo$, in quanto la $x$ di secondo grado si trova sotto ad una radice quadrata, e può essere quindi considerata dello stesso grado di infinito della $x$ di primo grado.
In questi casi risulta utile effettuare una sorta di razionalizzazione, moltiplicando e dividendo per una quantità in modo da eliminare la radice ed il segno meno, così da risolvere anche la situazione di indeterminazione.
In questo caso possiamo moltiplicare e dividere per $2x + sqrt(4x^2+x) $:
$2x – sqrt(4x^2+x) = 2x – sqrt(4x^2+x) * frac(2x + sqrt(4x^2+x))(2x + sqrt(4x^2+x)) $
Svolgiamo i calcoli:
$ frac( (2x – sqrt(4x^2+x))*(2x + sqrt(4x^2+x)))(2x + sqrt(4x^2+x)) =$
$frac( (2x)^2 – (sqrt(4x^2+x))^2 )(2x + sqrt(4x^2+x)) $
Svolgiamo i quadrati:
$frac( 4x^2 – 4x^2 – x )(2x + sqrt(4x^2+x)) = frac( – x )(2x + sqrt(4x^2+x))$
Applicando il limite, possiamo notare che siamo ancora in presenza di una forma indeterminata, questa volta del tipo $frac(oo)(oo)$; possiamo procedere mettendo in evidenza il termine $x$ sia al numeratore che al denominatore (all’interno della radice dobbiamo raccogliere $x^2$):
$ frac( – x )(2x + sqrt(4x^2+x)) = frac( – x )(2x + sqrt(x^2 (4 + frac(1)(x^2) ))$
Poiché nel nostro caso $ x to +oo$, possiamo portare $x^2$ fuori dalla radice senza valore assoluto, in quanto al limite $x$ sarà sicuramente positivo:
$ frac( – x )(2x + x*sqrt(4 + frac(1)(x^2) )$
Mettiamo in evidenza $x$ a numeratore e denominatore e semplifichiamo:
$ frac( – x )( x ( 2 + sqrt(4 + frac(1)(x^2) )) = frac( -1 )( 2 + sqrt(4 + frac(1)(x^2) ) $
Abbiamo eliminato ogni forma di indeterminazione, poiché l’unito termine in $x$ presenta $x$ al denominatore, che come sappiamo darà un contributo nullo al valore del limite.
Possiamo quindi procedere al calcolo del limite:
$ lim_(x to +oo) ( 2x – sqrt(4x^2+x) ) = lim_(x to +oo) frac( -1 )( 2 + sqrt(4 + frac(1)(x^2) ) = – 1/4 $
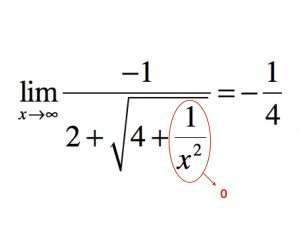
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(x to +oo) frac( sin(x) – cos(x) )(x) $
Il limite in questione non può essere calcolato mediante soluzioni note, in quanto si hanno delle funzioni periodiche di cui è impossibile calcolare l’andamento quando l’argomento tende ad infinito.
Facciamo alcune considerazioni sulla frazione di cui dobbiamo calcolare il limite; possiamo scrivere tale funzione come prodotto di due funzioni:
$ frac( sin(x) – cos(x) )(x) = 1/x * ( sin(x) – cos(x) )$
Con questa scrittura possiamo ragionare sulle singole funzioni; il primo fattore, ovvero $1/x$ è un’iperbole, di cui sappiamo calcolare il limite:
$ lim_(x to oo) 1/x = 0 $
Per quanto riguarda il secondo fattore, invece, non risulta immediato il valore del limite, o meglio non si può determinare il suo valore; sappiamo, però, che le funzioni seno e coseno sono limitate, e in particolare:
$ -1 <= sin(x) <= 1 , -1 <= cos(x) <= 1$
Di conseguenza, certamente anche la funzione $sin(x) – cos(x) $ è una funzione limitata, in quanto somma di funzioni limitate.
Possiamo, quindi, trattare la funzione al numeratore, all’interno del nostro limite, come una costante, essendo una funzione limitata.
Con questi presupposti, possiamo concludere che il limite avrà il seguente valore:

$ lim_(x to oo) frac( sin(x) – cos(x) )(x) = 1/x * ( sin(x) – cos(x) ) = 0 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite di funzione: $ lim_(x to pi/4) frac( sin(x) – cos(x) )( sin(4x) ) $
Il limite presenta una forma indeterminata del tipo $0/0$, infatti sostituendo $π/4$ ad $x$ nella funzione otteniamo:
$ frac( sin(π/4) – cos(π/4) )( sin(4*π/4) ) = frac( frac(sqrt2)(2) – frac(sqrt2)(2) )( sin(π) ) = 0/0 $
Procediamo, quindi, cercando di eliminare tale forma di indeterminazione; a tal proposito, possiamo moltiplicare numeratore e denominatore per $ sin(x) + cos(x) $, e cercare di semplificare qualche fattore:
$ frac( sin(x) – cos(x) )( sin(4x) ) * frac(sin(x) + cos(x))(sin(x) + cos(x)) $
Moltiplicando otteniamo:
$ frac( (sin(x) – cos(x))(sin(x) + cos(x)))( sin(4x)*(sin(x) + cos(x))) = frac( sin^2(x) – cos^2(x) )( sin(4x)*(sin(x) + cos(x))) $
Dalla relazione fondamentale, ricordando la relazione tra seno e coseno, abbiamo:
$ frac( sin^2(x) – cos^2(x) )( sin(4x)*(sin(x) + cos(x))) = frac( 1 -cos^2(x) – cos^2(x) )( sin(4x)*(sin(x) + cos(x))) = $
$ frac( 1 – 2cos^2(x) )( sin(4x)*(sin(x) + cos(x))) $
Ricordiamo che vale la seguente relazione per la formula di duplicazione del coseno:
$ cos(2x) = 2cos^2(x) – 1 $
Nel nostro caso si ha quindi:
$ frac( 1 – 2cos^2(x) )( sin(4x)*(sin(x) + cos(x))) = frac( – cos(2x) )( sin(4x)*(sin(x) + cos(x)))$
Passiamo ora al denominatore; ricordiamo che la formula di duplicazione del seno è la seguente:
$ sin(2x) = 2 sin(x) cos(x) $
Nel nostro caso la formula da applicare è la seguente:
$ sin(4x) = sin(2 * 2x) = 2 sin(2x) cos(2x) $
Sostituendo alla funzione:
$ frac( – cos(2x) )( sin(4x)*(sin(x) + cos(x))) = frac( – cos(2x) )( 2 sin(2x) cos(2x)*(sin(x) + cos(x)))$
Notiamo che è possibile semplificare il termine $ cos(2x) $, ed eliminare così la forma indeterminata:
$ frac( – cos(2x) )( 2 sin(2x) cos(2x)*(sin(x) + cos(x))) = frac( – 1 )( 2 sin(2x)*(sin(x) + cos(x))) $
Torniamo ora al limite:
$ lim_(x to π/4) frac( sin(x) – cos(x) )( sin(4x) ) = lim_(x to π/4) frac( – 1 )( 2 sin(2x)*(sin(x) + cos(x))) $
Poiché la funzione è ora definita in $ x = π/4$, per determinare il valore del limite possiamo semplicemente sostituire $π/4$ nella funzione:
$ lim_(x to π/4) frac( – 1 )( 2 sin(2x)*(sin(x) + cos(x))) = $
$ frac( – 1 )( 2 sin(2*π/4)*(sin(π/4) + cos(π/4))) = $
$ frac( – 1 )( 2 sin(π/2)*( frac(sqrt2)(2) + frac(sqrt2)(2) )) = $
$ frac( – 1 )( 2 * 1*( sqrt2)) = – frac(1)( 2 sqrt2) $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite di funzione: $ lim_(x to 0) frac( cos(x) – cos(2x) )( 1 – cos(x) ) $
Il limite presenta una forma di indeterminazione del tipo $0/0$, in quanto sostituendo si trova:
$ frac( cos(x) – cos(2x) )( 1 – cos(x) ) = frac( cos(0) – cos(2*0) )( 1 – cos(0) ) = frac(1-1)(1-1) = 0/0 $
Possiamo cercare di eliminare la forma indeterminata sviluppando $cos(2x)$, ricordando che vale la seguente uguaglianza:
$ cos(2x) = 2cos^2(x) – 1$
Sostituendo alla nostra funzione si ottiene:
$ frac( cos(x) – cos(2x) )( 1 – cos(x) ) = frac( cos(x) – [2cos^2(x) – 1] )( 1 – cos(x) ) = $
$ frac( cos(x) – 2cos^2(x) + 1 )( 1 – cos(x) ) $
Cerchiamo ora di fattorizzare il numeratore in modo da poter ottenere dei fattori che possano essere semplificati con il denominatore; scriviamo, quindi, $ 2cos^2(x) $ come $ cos^2(x) + cos^2(x) $:
$ frac( cos(x) – 2cos^2(x) + 1 )( 1 – cos(x) ) = frac( cos(x) – cos^2(x) – cos^2(x) + 1 )( 1 – cos(x) ) $
Effettuiamo un raccoglimento parziale tra i primi due termini, mentre per i secondi due notiamo che possono essere scritti come prodotto di somma e differenza di due quadrati:
$ frac( cos(x) [ 1 – cos(x)] – [cos^2(x) – 1] )( 1 – cos(x) ) = $
$frac( cos(x) [ 1 – cos(x)] – [cos^2(x) – 1] )( 1 – cos(x) ) =$
$ frac( cos(x) [ 1 – cos(x)] – [(cos(x) – 1)(cos(x) + 1)] )( 1 – cos(x) ) $
Cambiamo segno al secondo termine:
$ frac( cos(x) ( 1 – cos(x)) + (1 – cos(x))(cos(x) + 1) )( 1 – cos(x) ) $
Notiamo che abbiamo ottenuto il risultato desiderato: possiamo semplificare per $(1 – cos(x))$ ed eliminare così la forma indeterminata:
$ frac( cos(x) ( 1 – cos(x)) + (1 – cos(x))(cos(x) + 1) )( 1 – cos(x) ) = $
$ cos(x) + (cos(x) + 1) = 2cos(x) + 1$
Passiamo ora al limite, di cui possiamo facilmente determinare il valore:
$ lim_(x to 0) frac( cos(x) – cos(2x) )( 1 – cos(x) ) = lim_(x to 0) 2cos(x) + 1 = $
$ 2cos(0) + 1 = 2 + 1 = 3 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite di funzione: $ lim_(x to 0) frac( x^2 – sin^2(x) )( x^2 + sin(x^2) ) $
Il limite proposto presenta una forma di indeterminazione del tipo $0/0$, in quanto si ha che:
$ frac( 0^2 – sin^2(0) )( 0^2 + sin(0^2) ) = 0/0 $
Data la presenza della funzione $sin(x)$, e poiché il limite si ha per $x to 0$, possiamo cercare di risolvere l’esercizio cercando di ricondurci al limite notevole seguente:
$ lim_(x to 0) frac( sin(x) )( x ) = 1 $
In questo caso, è conveniente procedere raccogliendo al numeratore e al denominatore della frazione il termine $x^2$:
$ frac( x^2 – sin^2(x) )( x^2 + sin(x^2) ) = frac( x^2 ( 1 – frac(sin^2(x))(x^2)) )( x^2 ( 1 + frac(sin(x^2))(x^2)) ) $
Possiamo inoltre semplificare la frazione eliminando $x^2$:
$ frac( x^2 ( 1 – frac(sin^2(x))(x^2) ))( x^2 ( 1 + frac(sin(x^2))(x^2) )) = frac( 1 – frac(sin^2(x))(x^2) )( 1 + frac(sin(x^2))(x^2) ) $
Al numeratore è presente il termine $frac(sin^2(x))(x^2) $ che può essere scritto come $(frac(sin(x))(x))^2$.
Passiamo quindi al limite:
$ lim_(x to 0) frac( x^2 – sin^2(x) )( x^2 + sin(x^2) ) = lim_(x to 0) frac( 1 – (frac(sin(x))(x))^2 )( 1 + frac(sin(x^2))(x^2) ) $
Ogni forma di indeterminazione è stata eliminata, e ricorrendo al limite notevole accennato precedentemente, possiamo calcolare il valore del limite:
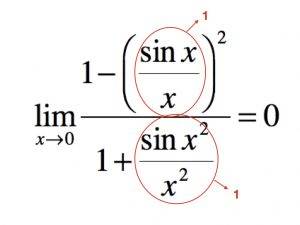
Concludiamo che il limite vale $0$:
$ lim_(x to 0) frac( 1 – (frac(sin(x))(x))^2 )( 1 + frac(sin(x^2))(x^2) ) = frac(1-1)(1+1) = 0/2 = 0 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite di funzione: $ lim_(x to 0) frac( x^2 + sin^2(x) )( x^2 + sin(x^2) ) $
Il limite proposto presenta una forma di indeterminazione del tipo $0/0$, in quanto si ha che:
$ frac( 0^2 + sin^2(0) )( 0^2 + sin(0^2) ) = 0/0 $
Data la presenza della funzione $sin(x)$, e poiché il limite si ha per $x to 0$, possiamo cercare di risolvere l’esercizio cercando di ricondurci al limite notevole seguente:
$ lim_(x to 0) frac( sin(x) )( x ) = 1 $
In questo caso, è conveniente procedere raccogliendo al numeratore e al denominatore della frazione il termine $x^2$:
$ frac( x^2 + sin^2(x) )( x^2 + sin(x^2) ) = frac( x^2 ( 1 + frac(sin^2(x))(x^2)) )( x^2 ( 1 + frac(sin(x^2))(x^2)) ) $
Possiamo inoltre semplificare la frazione eliminando $x^2$:
$ frac( x^2 ( 1 + frac(sin^2(x))(x^2) )( x^2 ( 1 + frac(sin(x^2))(x^2) ) = frac( 1 + frac(sin^2(x))(x^2) )( 1 + frac(sin(x^2))(x^2) ) $
Al numeratore è presente il termine $frac(sin^2(x))(x^2) $ che può essere scritto come $(frac(sin(x))(x))^2$.
Passiamo quindi al limite:
$ lim_(x to 0) frac( x^2 + sin^2(x) )( x^2 + sin(x^2) ) = lim_(x to 0) frac( 1 + (frac(sin(x))(x))^2 )( 1 + frac(sin(x^2))(x^2) ) $
Ogni forma di indeterminazione è stata eliminata, e ricorrendo al limite notevole accennato precedentemente, possiamo calcolare il valore del limite:
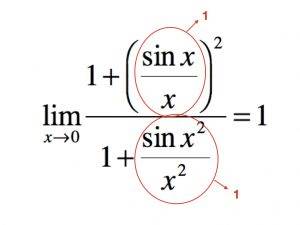
Concludiamo che il limite vale $1$:
$ lim_(x to 0) frac( 1 + (frac(sin(x))(x))^2 )( 1 + frac(sin(x^2))(x^2) ) = frac(1+1)(1+1) = 2/2 = 1 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite di funzione: $ lim_(x to π) frac( sqrt(1+sin(x)) – sqrt(1-sin(x)) )( sin^2(x) ) $
Il limite proposto presenta una forma di indeterminazione del tipo $0/0$, in quanto si ha che:
$ frac( sqrt(1+sin(0)) – sqrt(1-sin(0)))( sin^2(0) ) = frac(1-1)(0) = 0/0 $
Per eliminare l’indeterminazione e determinare il valore del limite, possiamo razionalizzare la frazione, moltiplicando numeratore e denominatore per $sqrt(1+sin(x)) + sqrt(1-sin(x)) $:
$ frac( [sqrt(1+sin(x)) – sqrt(1-sin(x))] * [sqrt(1+sin(x)) + sqrt(1-sin(x))] )( sin^2(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) $
Svolgiamo i calcoli al numeratore:
$ frac( [sqrt(1+sin(x))]^2 – [sqrt(1-sin(x))]^2 )( sin^2(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) = $
$ frac( 1+sin(x) – 1 + sin(x) )( sin^2(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) = $
$ frac( 2 sin(x) )( sin^2(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) = $
Possiamo semplificare $sin(x)$:
$ frac( 2 sin(x) )( sin^2(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) = frac( 2 )( sin(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) $
Notiamo che in questo modo abbiamo eliminato la forma indeterminata; infatti, passando al limite, si ha:
$ lim_(x to π) frac( 2 )( sin(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) $
L’espressione tra parentesi quadra da come contributo $2$, poiché, sostituendo $π$ nelle funzioni:
$ sqrt(1+sin(π)) + sqrt(1-sin(π)) = sqrt(1) + sqrt(1) = 1+1 = 2$
Mentre il primo fattore del prodotto al denominatore, cioè $sin(x)$, da come contributo $0$, in quanto $ sin(π) = 0$; il limite, quindi, può essere facilmente calcolato:
$ lim_(x to π) frac( 2 )( sin(x) * [sqrt(1+sin(x)) + sqrt(1-sin(x))] ) = $
$ lim_(x to π) frac( 2 )( sin(x) * 2 ) = oo $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite di funzione: $ lim_(x to 0) frac(sin(2x))(sin(3x)) $
Il limite proposto presenta una forma di indeterminazione del tipo $0/0$; per eliminarla e determinare il valore del limite, possiamo ricordare di un limite notevole che coinvolge la funzione $sin(x)$, ed è il seguente:
$ lim_(x to 0) frac(sin(x))(x) = 1 $
Possiamo cercare di ricondurre la funzione $frac(sin(2x))(sin(3x)) $ a una funzione equivalente in modo da poter sfruttare il limite notevole; cominciamo, per esempio, moltiplicando e dividendo per x:
$ frac(sin(2x))(sin(3x)) = frac(sin(2x))(sin(3x)) * x/x = $
$ frac(sin(2x))(x) * frac(x)(sin(3x))$
Notiamo che la funzione assume una forma che ricorda quella del limite notevole; dobbiamo però tener presente che l’argomento del seno è dato da $x$ moltiplicato per un fattore e tale fattore deve essere presente anche al denominatore.
Procediamo, quindi, moltiplicando e dividendo per 6:
$ frac(sin(2x))(x) * frac(x)(sin(3x)) = frac(sin(2x))(x) * frac(x)(sin(3x)) * 6/6 = $
$ frac(sin(2x))(x) * frac(x)(sin(3x)) * 2/2 * 3/3 = $
$ frac(sin(2x))(2x) * frac(3x)(sin(3x)) * 2/3 $
Passiamo ora al limite:
$ lim_(x to 0) frac(sin(2x))(sin(3x)) = lim_(x to 0) frac(sin(2x))(2x) * frac(3x)(sin(3x)) * 2/3 $
I primi due fattori possono essere ricondotti al limite notevole discusso precedentemente, e tendono quindi ad 1:
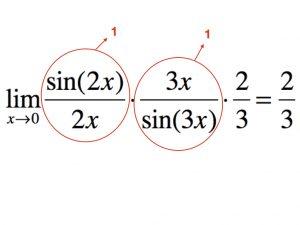
Concludiamo, quindi, che il valore del limite è $2/3$:
$ lim_(x to 0) frac(sin(2x))(2x) * frac(3x)(sin(3x)) * 2/3 = 2/3 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(n to +oo) frac(log(n))( 1 + sqrt(n) ) $
Il limite si presenta in un forma indeterminata del tipo $frac(+oo)(+oo)$; in questo caso, poiché è presente un logaritmo al numeratore e una potenza al denominatore, possiamo cercare di sfruttare il limite notevole seguente:
$ lim_(n to +oo) frac(log(n))( n^k ) = 0 $
Possiamo procedere effettuando un raccoglimento totale al denominatore, mettendo in evidenza il termine $sqrt(n)$:
$ lim_(n to +oo) frac(log(n))( 1 + sqrt(n) ) = lim_(n to +oo) frac(log(n))( sqrt(n) (1/sqrt(n) + 1) ) $
In questo modo, abbiamo il limite nella forma cercata; applicando le proprietà algebriche dei limiti, infatti, possiamo scrivere il nostro limite in una forma equivalente:
$ lim_(n to +oo) frac(log(n))( sqrt(n)) * lim_(n to +oo) frac(1)(1/sqrt(n) + 1 ) $
Il primo limite, quindi, corrisponde al limite notevole visto in precedenza, ed è quindi uguale a zero; il secondo termine, invece, presenta al denominatore la somma di due termini, di cui uno tendente a zero. Il secondo limite vale quindi 1.
Il valore del limite iniziale è quindi il seguente:
$ lim_(n to +oo) frac(log(n))( sqrt(n)) * lim_(n to +oo) frac(1)(1/sqrt(n) + 1 ) = 0 * 1 = 0 $
Potrebbe interessarti anche
- Appunti sui Limiti
Calcolare il valore del seguente limite: $ lim_(n to +oo) ( cot(1/n) )^( frac(1)(log(sin(1/n))) ) $
Il limite proposto si trova nella forma indeterminata del tipo $0^0$. Per poter eliminare la forma indeterminata e risolvere il limite, è conveniente esprimere la potenza nella forma esponenziale, ovvero sfruttare la seguente relazione:
$ a^b = e^(b*log(a)) = exp(b*log(a)) $
Nel nostro caso, la successione diventa:
$ ( cot(1/n) )^( frac(1)(log(sin(1/n))) ) = e^( frac(1)(log(sin(1/n))) * log(cot(1/n)) ) $
per comodità scriveremo:
$ e^( frac(1)(log(sin(1/n))) * log(cot(1/n)) ) = exp(frac(1)(log(sin(1/n))) * log(cot(1/n))) $
Ora, trasformiamo il termine $log(cot(1/n)) $ in una forma equivalente, in modo da poterlo mettere in relazione con l’altro fattore.
Dalla relazione tra tangente e cotangente risulta che:
$log(cot(1/n)) = log( frac(1)(tg(1/n)) ) $
e dalla proprietà dei logaritmi:
$ log( frac(1)(tg(1/n)) ) = log( (tg(1/n))^(-1) ) = – log( tg(1/n) ) $
Sapendo che la tangente di un angolo si esprime come rapporto di seno e coseno di quell’angolo, possiamo scrivere:
$ – log( tg(1/n) ) = – log( frac(sin(1/n))(cos(1/n)) ) $
e dalle proprietà algebriche dei logaritmi, sappiamo che il logaritmo di un rapporto equivale alla differenza tra logaritmo del numeratore e logaritmo del denominatore:
$ – log( frac(sin(1/n))(cos(1/n)) ) = – [log(sin(1/n)) – log(cos(1/n))] = $
$ – log(sin(1/n)) + log(cos(1/n)) $
Tornando alla successione, e applicando tali modifiche al secondo fattore, si ottiene:
$ exp(frac(1)(log(sin(1/n))) * log(cot(1/n))) = exp(frac(1)(log(sin(1/n))) * [- log(sin(1/n)) + log(cos(1/n))]) $
Ovvero:
$ exp( frac( – log(sin(1/n)) + log(cos(1/n)) )(log(sin(1/n)))) = $
$ exp(frac(-log(sin(1/n)))(log(sin(1/n))) + frac(log(cos(1/n)))(log(sin(1/n)))) = $
$ exp( – 1 + frac( log(cos(1/n)) )(log(sin(1/n)) )) $
Consideriamo la frazione che compare nell’esponenziale; per $n to oo$, sappiamo che $ 1/n to 0$, e poiché tale espressione è argomento di funzioni goniometriche, siamo in grado di calcolare tali limiti; in particolare, il numeratore tende a $0$, poiché $ cos(0) = 1$, e tale valore è argomento di un logaritmo, mentre il denominatore tende a $-oo$, poiché $ sin(0) = 0$, e al limite il logaritmo tende a $-oo$ e il suo argomento tende a zero.
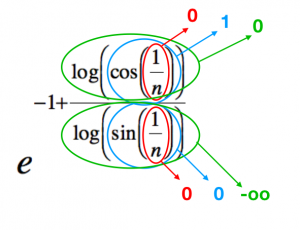
Quindi, passando al limite abbiamo:
$ lim_(n to oo) exp( – 1 + frac( log(cos(1/n)) )(log(sin(1/n)) )) = e^(-1) = 1/e $
Potrebbe interessarti anche
- Appunti sui Limiti di successione
- Appunti sui Limiti
