Punto di massimo relativo

Consideriamo la funzione $ y = f(x) $, definita in un intervallo $ I $. Se $ c $ è un punto dell’intervallo $ I $, si dice che $ c $ è un punto di massimo relativo per la funzione $ f(x) $ se esiste un intorno di  $ c $, contenuto in $ I $, tale che, per tutti i punti $ x $ di tale intorno, si abbia: \[ f(x) \le f(c) \]

Quindi, il valore $ f(c) $ è il valore massimo che la funzione assume nell’intorno considerato di  $ c $, e quindi $ f(c) $ viene definito massimo relativo della funzione $ f(x) $.

Punto di minimo relativo

Consideriamo sempre una generica funzione $ y = f(x) $, definita in un intervallo $ I $. Se $ c $ è un punto dell’intervallo $ I $, diciamo che $ c $ è un punto di minimo relativo per la funzione $ f(x) $ se esiste un intorno di $ c $, contenuto in $ I $, tale che, per tutti i punti $ x  $di tale intorno, si ha: \[ f(x) \ge f(c) \]

Quindi, in questo caso, il valore $ f(c) $ è il valore minimo che la funzione assume nell’intorno considerato di $ c $, e quindi $ f(c) $ viene definito minimo relativo della funzione $ f(x) $.

I punti $ c $ di massimo e minimo vengono anche definiti punti estremanti per la funzione, e i loro corrispettivi valori $ f(c) $ si definiscono estremi relativi.

In particolare, i massimi e i minimi relativi vengono anche definiti massimi e minimi locali, in quanto si riferiscono solo ad un particolare intorno del punto $ c $, e non in tutto l’intervallo $ I $, in cui la funzione può avere più di un punto di massimo o minimo relativo.

Estremi relativi forti e deboli

Consideriamo la funzione $ y = f(x) $, definita in un intervallo  $ I $, e sia $ c $ un punto di massimo relativo per $ f(x) $. Ciò significa che esiste un intorno di $ c $ in cui \( f(x) \le f(c) \). Se esiste un intorno di $ c $ per tutti gli  $ x $ del quale (escluso al più $ x = c $) si ha: \[ f(x) \lt f(c) \]

allora $ c $ viene definito punto di massimo relativo forte (o proprio) e $ f(c) $ di dice massimo relativo forte.

Altrimenti, $ c $ si definisce punto di massimo relativo debole (o improprio), e $ f(c) $ è un massimo relativo debole.

Allo stesso modo, se esiste un intorno di $ c $ in cui per tutti gli $ x $ di tale intorno (escluso al più $ x = c $) si ha: \[ f(x) \gt f(c) \]

$ c $ viene definito punto di minimo relativo forte (o proprio) e $ f(c) $ si dice minimo relativo forte.

In caso contrario, $ c $ si definisce punto di minimo relativo debole (o improprio), e $ f(c) $ è un minimo relativo debole.

Il punto di flesso

Consideriamo una funzione $ y = f(x) $; se esiste la retta, non parallela all’asse $ y $, tangente al grafico della funzione nel punto $ (x_0 ; f(x_0)) $, e se esiste un intorno di $ x_0 $, che indichiamo \( (x_0 – \delta; x_0 + \delta) \) in cui la funzione, in corrispondenza dell’intorno destro e sinistro, si trovi in parti opposte rispetto alla retta tangente, allora il punto $ (x_0 ; f(x_0)) $ è un flesso della curva di equazione $ y = f(x) $.

In particolare, ricordiamo che se la funzione è derivabile nel punto $ x_0 $, la retta tangente ha equazione: \[ t(x) = f'(x_0)(x-x_0)+f(x_0) \]

In base alla posizione della funzione rispetto alla retta tangente e agli interni destro e sinistro, possiamo classificare i flessi in flessi ascendenti e discendenti.

Nel caso in cui si abbia

\( \begin{cases} f(x) \le t(x) \text{ per } x_0 – \delta \lt x \lt x_o \\ f(x) \ge t(x) \text{ per } x_0 \lt x \lt x_0 + \delta \end{cases}  \)

il flesso è ascendente.

Altrimenti, se abbiamo:

\( \begin{cases} f(x) \gt t(x) \text{ per } x_0 – \delta \lt x \lt x_0 \\ f(x) \le t(x) \text{ per } x_0 \lt x \lt x_0 + \delta \end{cases} \)

allora, il flesso è discendente.

Il teorema di De L’Hopital presenta le seguenti ipotesi: si considerano due funzioni f(x) e g(x) definite e derivabili in tutti i punti di un intorno I di un punto c (finito o infinito), escluso al più c stesso; se il limite del rapporto per x che tende a c delle funzioni si presenta in una forma indeterminata del tipo [0/0] o \( [\infty/\infty]\), se la derivata della funzione g(x) è diversa da zero in tutti i punti di I, escluso x = c, e se esiste il limite per \( x \rightarrow c \) del rapporto delle derivate delle funzioni, allora esiste anche il limite, per \( x \rightarrow c \), del rapporto delle funzioni stesse, e i due limiti coincidono:

\[ \lim_{x \rightarrow c} \frac{f(x)}{g(x)} = \lim_{x \rightarrow c} \frac{f'(x)}{g'(x)} \]

Da questo teorema possiamo ricavare una regola molto utile, da applicare per risolvere certi limiti che si presentano nelle forme indeterminate sopra elencate; tale regola viene definita regola di De L’Hopital:

• Il limite del rapporto di due funzioni, che si presenta nella forma indeterminata [0/0] o \( [\infty/\infty] \), è uguale al limite del rapporto delle loro derivate , purché siano soddisfatte tutte le ipotesi del teorema.

In particolare, il teorema e la regola di De L’Hopital sono validi considerando il limite per x che tende a c, sia nel caso in cui c è un valore finito, sia nel caso in cui esso sia un valore infinito.

Inoltre, se c è un valore finito, il teorema vale anche se I è un intorno solamente destro, o solamente sinistro di c.

Ci sono alcuni casi, poi, in cui capita che anche il limite per \( x \rightarrow c \) delle derivate delle funzioni si presenti in una forma indeterminata del tipo [0/0] o \( [\infty/\infty] \):

\( \displaystyle \lim_{x \rightarrow c} \frac{f'(x)}{g'(x)} = \frac{0}{0} \text{ oppure } \lim_{x \rightarrow c} \frac{f'(x)}{g'(x)} = \frac{\infty}{\infty} \)

in questo caso, la regola di De L’Hopital può essere applicata nuovamente sul rapporto delle derivate, e in questo caso si ha che:

\( \displaystyle \lim_{x \rightarrow c} \frac{f(x)}{g(x)} = \lim_{x \rightarrow c} \frac{f'(x)}{g'(x)} = \lim_{x \rightarrow c} \frac{f”(x)}{g”(x)} \)

Quindi, il teorema può essere applicato ripetutamente, finché non si giunge ad un limite che non si trova più in una forma indeterminata.

Applicazioni al confronto di particolari infiniti

Il teorema di De L’Hopital può essere applicato allo studio di infiniti particolari. Consideriamo, per esempio, la funzione logaritmica, \( y = \log x \), e paragoniamola alla funzione $ y = x $. Studiamo, quindi, il seguente limite:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{\log x}{x^{\alpha}} \)

cercando di capire se esiste un esponente di x positivo per cui il limite sia finito e non nullo.

Poiché il limite si presenta nella forma indeterminata \( [\infty/\infty] \), possiamo applicare il teorema di De L’Hopital:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{\log x}{x^{\alpha}} = \lim_{x \rightarrow +\infty} \frac{\frac{1}{x}}{\alpha \cdot x^{\alpha – 1}} = \lim_{x \rightarrow +\infty} \frac{1}{\alpha \cdot x^{\alpha}} = 0 \)

Possiamo quindi affermare che il limite sopra scritto è sempre nullo:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{\log x}{x^{\alpha}} = 0 \text{, } \forall \alpha \in \mathbb{R^{+}} \)

Questo ci permette di dire che il logaritmo in base $ e $ è un infinito di ordine inferiore a qualsiasi potenza di x ad esponente positivo, e quindi non esiste un numero che possa esprimerne l’ordine di grandezza.

Similmente, possiamo studiare la funzione esponenziale $ y = e^x $, calcolando il seguente limite:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{e^x}{x^{\alpha}} \)

Poiché, anche in questo caso il limite si presenta nella forma indeterminata $[\infty/\infty]$, possiamo applicare il teorema di De L’Hopital:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{e^x}{x^{\alpha}} = \lim_{x \rightarrow +\infty} \frac{e^x}{\alpha \cdot x^{\alpha-1}} \)

Notiamo che, essendo la derivata di $ e^x $ sempre $ e^x $, non abbiamo cambiamenti al numeratore, e al denominatore abbiamo sempre potenze di x; dobbiamo, quindi, applicare il teorema finché al denominatore non resta un fattore che moltiplica x:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{e^x}{\alpha \cdot x^{\alpha-1}} = \ldots = \lim_{x \rightarrow +\infty} \frac{e^x}{k \cdot x} =\lim_{x \rightarrow +\infty} \frac{e^x}{k} = +\infty \)

Quindi, il limite precedente vale sempre più infinito:

\( \displaystyle \lim_{x \rightarrow +\infty} \frac{e^x}{x^{\alpha}} = +\infty, \,\,\, \forall \alpha \in \mathbb{R^{+}} \)

Possiamo, quindi, affermare che l’esponenziale $ e^x $ è un infinito di ordine superiore a qualsiasi potenza di x ad esponente positivo, e quindi, anche in questo caso, non esiste un numero che ne esprima l’ordine di infinito.

Funzioni crescenti e decrescenti in un intervallo

Una funzione y = f(x) definita in un intervallo I, limitato o illimitato, si dice strettamente crescente in I (o semplicemente crescente in I) se:

\[ \forall x_1, x_2 \in I\,\,, \,\, x_1 \lt x_2 \rightarrow f(x_1) \lt f(x_2) \]

Invece, la funzione f(x) si dice strettamente decrescente in I (o semplicemente decrescente in I ) se accade che:

\[ \forall x_1, x_2 \in I \,\,, \,\, x_1 \lt x_2 \rightarrow f(x_1) \gt f(x_2) \]

Vediamo ora un teorema che è una conseguenza del teorema di Lagrange, e mette in relazione la crescenza o la decrescenza di una funzione con il segno della sua derivata; ciò ci permette di determinare gli intervalli di monotonia di una funzione cioè gli intervalli in cui la funzione è crescente o decrescente.

Teorema

Consideriamo una funzione y = f(x) continua in un intervallo I (limitato o illimitato) e derivabile nei punti interni di I. Se la derivata della funzione è sempre positiva in I, allora la funzione è crescente in I; se, invece, la derivata della funzione è sempre negativa in I, allora la funzione è decrescente in I.

Possiamo quindi dire che il fatto che una funzione abbia derivata positiva, o negativa, nei punti interni di un intervallo I è condizione sufficiente per affermare che la funzione è crescente o decrescente in quell’intervallo.

Il teorema precedente può essere invertito, e si ha il seguente:

Teorema

Data una funzione y = f(x) continua in un intervallo I e derivabile nei punti interni di tale intervallo, se f(x) è crescente in I, allora nei punti interni di I la sua derivata è positiva: \( f’(x) \ge 0 \); altrimenti, se f(x) è decrescente in I, la sua derivata è negativa nei punti interni di I, cioè \( f’(x) \le 0 \).

Esempio

Consideriamo la seguente funzione, e stabiliamo in quali intervalli essa è crescente, e in quali è decrescente:

\[ y = f(x) = \frac{x}{1+x^2} \]

Notiamo che la funzione è definita in tutto R, quindi l’unione degli intervalli in cui la funzione è crescente e decrescente è uguale a R. Come abbiamo visto in precedenza, poiché la crescenza e la decrescenza di una funzione sono legate al segno della derivata, calcoliamo la derivata della funzione.

Applichiamo la regola vista nel caso in cui la funzione è data dal rapporto di due funzioni:

\( f'(x) = \frac{1+x^2-x\cdot 2x}{(1+x^2)^2} =\frac{1+x^2-2x^2}{(1+x^2)^2} =\frac{1-x^2}{(1+x^2)^2} \)

Studiamo ora il segno della derivata, e cerchiamo gli intervalli in cui essa è positiva; risolviamo, quindi, la seguente disequazione:

\[ f'(x) \ge 0 \rightarrow \frac{1-x^2}{(1+x^2)^2} \ge 0 \]

Poiché il denominatore, essendo il quadrato di una somma di quadrati, è sempre positivo, e non si annulla mai, il segno della frazione è dato dal segno del numeratore:

\[ 1 – x^2 \ge 0 \]

La disequazione è risolta per valori interni all’intervallo delle radici; quindi, la derivata della funzione f(x) è positiva nel seguente intervallo:

\[ -1 \le x \le 1 \]

E, in questo intervallo, quindi, la funzione è crescente.

Di conseguenza, essendo la derivata della funzione negativa per \( x \lt -1 \text{ e } x \lt 1 \), in tali intervalli la funzione è decrescente.

Teorema di Cauchy

Nel teorema di Cauchy, si considerano due funzioni y = f(x) e y = g(x), entrambe continue nell’intervallo chiuso [a;b] e derivabili nell’intervallo aperto (a;b). Se la funzione g(x) ammette derivata diversa da zero in tutti i punti dell’intervallo (a;b), allora esiste un punto c, interno all’intervallo, nel quale si ha che:

\[ \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)} \]

Questo teorema viene anche definito teorema degli accrescimenti finiti, in quanto esso esprime che, se due funzioni soddisfano le condizioni indicate, allora il rapporto tra gli incrementi delle due funzioni in un intervallo indicato è uguale al rapporto delle derivate delle funzioni calcolate in uno stesso punti interno all’intervallo.

Il teorema di Lagrange, o del valor medio, afferma che, data una funzione y = f(x) continua nell’intervallo chiuso e limitato [a;b], e derivabile nell’intervallo aperto (a;b), esiste almeno un punto c, interno all’intervallo [a;b], tale che si abbia:

\[ \frac{f(b)-f(a)}{b-a} = f'(c) \]

Il teorema, quindi, esprime l’uguaglianza tra il rapporto incrementale della funzione nell’intervallo [a;b] e la derivata della funzione in un punto c, interno all’intervallo.

Interpretiamo, ora, il teorema di Lagrange dal punto di vista geometrico.

Consideriamo una curva di equazione y = f(x), e chiamiamo AB l’arco di questa funzione i cui estremi hanno ascisse a e b. Come sappiamo, il coefficiente angolare della retta AB è dato dal quoziente della differenza delle ascisse e la differenza delle ordinate di due punti qualsiasi appartenenti alla retta.

In questo caso, considerando i punti A e B, e sapendo che essi hanno coordinate, rispettivamente, (a; f(a)) e (b; f(b)), il coefficiente angolare della retta AB è dato da:

\[ m_{AB} = \frac{y_b – y_A}{x_B – x_A} = \frac{f(b)-f(a)}{b-a} \]

Dal teorema di Lagrange, abbiamo che m = f’(c), dove c è un punto interno all’intervallo [a;b]; sapendo che f’(c) è il coefficiente angolare della retta tangente alla curva in un punto P, possiamo affermare che tale retta è parallela alla retta passante per i punti A e B.

Applicazioni del teorema di Lagrange

Vediamo alcuni teoremi che ci illustrano delle applicazioni del teorema di Lagrange:

Teorema: Se una funzione continua ha derivata nulla in tutti i punti di un intervallo I (limitato, o illimitato ), allora essa è costante in quell’intervallo.

Teorema: Se due funzioni continue f(x) e g(x) hanno derivate uguali in tutti i punti di un intervallo, esse differiscono per una costante.

Infatti, se chiamiamo F(x) la differenza tra le funzioni f(x) e g(x), cioè:

\[ F(x) = f(x) – g(x) \]

sappiamo che la sua derivata è data dalla somma algebrica delle derivate delle singole funzioni:

\[ F'(x) = f'(x) – g'(x) \]

ma, dal momento che le derivate di f(x) e g(x) sono uguali in tutti i punti dell’intervallo considerato, abbiamo che:

\[ f'(x) = g'(x) \Rightarrow f'(x) – g'(x) = 0 \]

e quindi, anche $ F’(x) = 0 $; ciò significa che F(x) è una costante.

Consideriamo una funzione f(x) continua in un intervallo chiuso di estremi a e b, e derivabile nei punti interni di tale intervallo; se la funzione assume valori uguali agli estremi a e b dell’intervallo, allora esiste almeno un punto c, interno all’intervallo, in cui la funzione ha derivata nulla, cioè tale che $  f’(c) = 0 $.

Possiamo schematizzare il teorema di Rolle in questo modo:

\( \left. \begin{array}{l} \text{$f(x)$ continua in } [a;b] \\ \text{$f(x)$ derivabile in } (a;b) \\ f(a) = f(b)\end{array} \right\} \Rightarrow \exists c \in (a;b) | f'(c) = 0 \)

Vediamo ora alcuni casi in cui si verificano le ipotesi del teorema di Rolle; chiamiamo m e M i valori minimo e massimo assunti dalla funzione nell’intervallo [a;b]:

• Se m = M, la funzione assume, in tutto l’intervallo, lo stesso valore, che corrisponde a m = M; la funzione è, quindi, la funzione costante, e in particolare, si avrà anche che f (c) = m = M. Pertanto, in tutti i punti dell’intervallo, e quindi anche in c, la derivata della funzione sarà nulla.

• Se \( m \lt M \), la funzione non è costante in [a;b]; in questo caso possiamo capire meglio il teorema di Rolle anche dal punto di vista geometrico. Sappiamo, infatti, che la derivata di una funzione in un punto rappresenta il coefficiente angolare della retta tangente alla funzione in quel punto; se in un intervallo [a;b] esiste un punto c tale che si ha $ f’(c) = 0 $, allora in quel punto la tangente alla funzione è parallela all’asse x.

Significa che F(x) è una costante.

Il differenziale di una funzione

Se consideriamo una funzione f(x), derivabile in un intervallo I, sappiamo che comunque preso un punto x in tale intervallo, e incrementando x di un valore h in modo che x + h appartenga ancora ad I, la frazione che ha per numeratore la differenza tra la funzione calcolata in x + h e la funzione calcolata in x, e per denominatore h, si dice rapporto incrementale; inoltre, sappiamo che il limite per h che tende a zero di tale rapporto è la derivata prima della funzione.

Ora, indichiamo con \( \Delta x \) l’incremento della variabile indipendente, cioè:

\( \Delta x = (x+h) – x = x +h – x = h \)

e con \( \Delta y \) l’incremento della variabile dipendente, cioè:

\( \Delta y = f(x+h) – f(x) \)

Per quanto detto prima, sappiamo che il limite per \( \Delta x \) che tende a zero del rapporto tra \( \Delta y \) e \( \Delta x \) corrisponde alla derivata della funzione:

\( \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) \)

Inoltre, dato che la funzione f(x) è derivabile, sappiamo che la derivata f’(x) esiste sempre; in base al valore di f’(x) possiamo stabilire la relazione tra gli incrementi, e in particolare abbiamo che:

• se \( f’(x)  \ne 0 \) , allora \( \Delta y \) e \( \Delta x \) sono infinitesimi dello stesso ordine;
• se \( f’(x) = 0 \), allora \( \Delta y \) è un infinitesimo di ordine superiore a \( \Delta x \).

Ricordando, poi, il concetto di scrittura fuori dal limite, possiamo scrivere il limite precedente in questo modo:

\( \frac{\Delta y}{\Delta x} = f'(x) + \epsilon(\Delta x) \)

dove, \( \epsilon \) è funzione di \( \Delta x \), e tale che il suo limite per \( \Delta x \) che tende a zero è zero.

Dalla relazione precedente, moltiplicando ambi i membri per ∆x, otteniamo:

\( \Delta y = f'(x) \cdot \Delta x + \epsilon ( \Delta x ) \cdot \Delta x \)

e l’espressione \( f’(x) \cdot  \Delta x \), che si indica con \( df(x) \), o con $ dy $, prende il nome di differenziale della funzione f(x) nel punto x, relativamente all’incremento \( \Delta x \).

Quindi, il differenziale di una funzione in un punto, in cui la funzione è derivabile, corrisponde al prodotto della derivata della funzione stessa per l’incremento della variabile indipendente:

\[ dy = f'(x) \cdot \Delta x \]

In particolare, se la funzione in questione è la funzione $ y = f(x) = x $, la sua derivata è uguale a 1, quindi il suo differenziale corrisponde all’incremento \( \Delta x \):

\( dx = \Delta x \Leftarrow \begin{cases} dy = f'(x) \cdot \Delta x = 1 \cdot \Delta x = \Delta x \\ dy = df(x) = dx \end{cases} \)

Quindi, poiché il differenziale della variabile indipendente coincide con il suo incremento, possiamo affermare che il differenziale di una funzione è il prodotto tra la derivata della funzione stessa per il differenziale della variabile indipendente:

\( dy = f'(x) \cdot dx \)

Operazioni con i differenziali

Possiamo calcolare il differenziale di funzioni in vari casi, per esempio nel caso di somma o differenza di funzioni, prodotto o quoziente di funzioni. Le regole di derivazione che valgono per la somma, la differenza, il prodotto e il quoziente di funzioni valgono anche per calcolare tali differenziali.

In particolare, esaminiamo i vari casi:

• Differenziale della somma algebrica di funzioni

Il differenziale della somma algebrica di due o più funzioni è uguale alla somma algebrica dei differenziali delle singole funzioni:

\( d[f(x)\pm g(x)] = df(x) \pm dg(x) \)

• Differenziale del prodotto di due (o più) funzioni

Il differenziale del prodotto di due funzioni è uguale alla somma del prodotto del differenziale della prima funzione per la seconda, più il prodotto della prima funzione per il differenziale della seconda:

\( d[f(x) \cdot g(x)] = df(x) \cdot g(x) + f(x) \cdot dg(x) \)

• Differenziale del quoziente di due funzioni

Il differenziale del quoziente di due funzioni è uguale ad una frazione che ha per denominatore il quadrato del divisore, e per numeratore il prodotto del differenziale del dividendo per il divisore diminuito del prodotto tra il dividendo e il differenziale del divisore:

\( d\Big[ \frac{f(x)}{g(x)} \Big] = \frac{df(x) \cdot g(x) – f(x) \cdot dg(x)}{[g(x)]^2} \)

Significato geometrico di differenziale

Consideriamo una funzione $ y = f(x) $, e la sua tangente $ t $ nel punto $ P [ x ; f(x) ] $.

Il differenziale della funzione f(x) nel punto x, relativo a un incremento h, è l’incremento che subisce l’ordinata di un punto, muovendosi sulla retta tangente al grafico della funzione nel punto $ P [x; f(x)] $, quando la sua ascissa passa da x a x + h.

Considerando la figura precedente, possiamo dire che il differenziale dy è rappresentato dall’incremento dell’ordinata del punto P (di ascissa x ), che si sposta lungo la tangente, fino ad arrivare al punto T, che ha ascissa x + h; il differenziale è, quindi, rappresentato dalla misura del segmento MT.

Come abbiamo visto in precedenza, considerando una funzione generica f(x), e calcolando il limite del rapporto incrementale per h che tende a zero, otteniamo la derivata della funzione, che indichiamo con $ f’(x) $: \[ \displaystyle \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{f(x)} = f'(x) \]

Se, ora, consideriamo la funzione $ f’(x) $, possiamo applicare lo stesso ragionamento effettuato per $ f(x) $, cioè possiamo calcolare il limite del rapporto incrementale di $ f’(x) $, per trovare la derivata di $ f’(x) $. Tale derivata viene definita derivata seconda, o derivata del secondo ordine di $ f(x) $, e si indica $ f’’(x) $: \[ \displaystyle \lim_{h \rightarrow 0} \frac{f'(x+h) – f'(x)}{h} = f”(x) \]

Allo stesso modo, possiamo continuare, determinando le derivate del terzo, quarto ordine, e così via.

Per tali derivate, e per le derivate successive, si parla di derivate di ordine superiore della $ f(x) $.

Esempio di derivate di ordini superiori

\( f(x) = 4x^3-9x^2+3x-1 \)

\( f'(x) = 12x^2 – 18x + 3 \)

\( f”(x) = 24x – 18 \)

\( f”'(x) = 24 \)

\( f^{IV}(x) = 0 \)

Esempio 2

\( f(x) = \sin (x) \)

\( f'(x) = \cos (x) \)

\( f”(x) = -\sin (x) \)

\( f”'(x) = -\cos (x) \)

\( f^{IV}(x) = \sin (x) \)

La derivata di una funzione in un punto rappresenta il coefficiente angolare della retta tangente alla funzione in quel punto. Sfruttando questa relazione, è possibile determinare l’equazione della retta tangente al grafico di una funzione $ f(x) $, conoscendo l’ascissa ($ x_0 $) del punto P in cui la retta è tangente alla curva.

Tale retta, infatti, dovrà soddisfare i seguenti requisiti:

• Sapendo che il punto P in cui la retta è tangente alla curva ha ordinata x0, e sapendo che tale punto appartiene alla curva $ f(x) $, sappiamo che la sua ordinata è $ f(x_0) $. Quindi, la retta in questione passa per il punto $ P(x_0 ; f(x_0)) $. La sua equazione sarà quindi del tipo: \[ y = f(x_0) = m (x-x_0) \]dove m indica il suo coefficiente angolare.
• Sapendo, poi, che la derivata della funzione nel punto x0 rappresenta proprio il coefficiente angolare della retta cercata, abbiamo: \[ m = f'(x_0) \]

Dalle relazioni precedenti, possiamo dare l’equazione della retta richiesta, ottenibile conoscendo l’ascissa del punto di tangenza, e la derivata della curva in questione in quel punto: \[ y = f'(x_0) \cdot (x-x_0) + f(x_0) \]

Notiamo che l’equazione precedente si riferisce ad una retta non parallela agli assi; infatti, se la retta fosse parallela all’asse $ y $, essa avrebbe equazione $ x = x_0 $.

In questo caso, la funzione non sarebbe derivabile in $ x_0 $, in quanto ammetterebbe derivata infinita.

Vediamo ora alcuni casi particolari, in cui nei punti in questione la funzione non è derivabile:

Punto angoloso

La funzione $ f(x) $ è continua in $ x_0 $, ma non è derivabile in $ x_0 $, per esempio nel caso in cui il rapporto incrementale relativo al punto $ x_0 $ non ha limite, in quanto sono diversi i limiti sinistro e destro.

In questo caso, infatti, anche le derivate destra e sinistra sono diverse, quindi la funzione non è derivabile in $ x_0 $, ma esisteranno due rette tangenti alla funzione nel punto $ x0 $, che prende il nome di punto angoloso.

Quindi: \[ {f’}_{+}(x) = l_1 \in \mathbb{R} \wedge {f’}_{-}(x) = l_2 \in \mathbb{R} \]

e si ha che: \[ l_1 \ne l_2 \]

Il punto angoloso si ha anche quando una delle due derivate nel punto $ x_0 $ (la derivata destra, o quella sinistra) è finita, e l’altra infinita, e viceversa.

\[ {f’}_{+}(x) = \pm \infty \wedge {f’}_{-}(x) = l \in \mathbb{R} \]

oppure:

\[ {f’}_{+}(x) = l \in\mathbb{R} \wedge {f’}_{-}(x) = \pm\infty \]

Cuspide

Può accadere che in un punto $ x_0 $, in cui la funzione non è derivabile, vi siano due rette tangenti coincidenti, che sono parallele all’asse $ y $; si dice che il punto $ x_0 $ è una cuspide, che può essere definita come un caso particolare di punto angoloso.

In questo caso, le derivate destra e sinistra sono entrambe infinite, ma con segno opposto.

\[ {{f’}_{+}(x) = +\infty \wedge {f’}_{-}(x) = -\infty \,\,\,\, \mbox{ oppure } \,\,\,\, {{f’}_{+}(x) = -\infty \wedge {f’}_{-}(x) = +\infty

Flesso a tangente verticale

La funzione $ f(x) $ non è derivabile nel punto $ x_0 $, in quanto i valori delle derivate, destra e sinistra, sono uguali, ma entrambi infiniti.

Abbiamo quindi che: \[ {f’}_{+}(x) = +\infty \wedge {f’}_{-}(x) = +\infty \]

oppure: \[ {f’}_{+}(x) = -\infty \wedge {f’}_{-}(x) = – \infty \]

Consideriamo una generica funzione $ y = f(x) $, invertibile; sappiamo, allora, che possiamo calcolare la sua inversa, che indicheremo con: \[ f^{-1}(x) = F(y) \]

Possiamo, inoltre, calcolare la derivata di una funzione inversa anche senza calcolare l’inversa stessa; infatti, vale il seguente teorema:

Teorema: La derivata di una funzione inversa è il reciproco della derivata della funzione data, in tutti i punti in cui quest’ultima ha derivata non nulla: \[ {f^{-1}}'(x) = F(y) = \frac{1}{f'(x)} \,\,\,\, , \,\,\,\, f'(x) \ne 0 \]

Esaminiamo, ora, alcune funzioni di cui già sappiamo calcolare la derivata, ma che possono essere considerate funzioni inverse di altre più semplici, o più semplicemente derivabili.

• Consideriamo la funzione radice n-esima, di equazione: \[ y = \sqrt[n]{x} \,\,\,\, , \,\,\,\, n \in \mathbb{N_0} \,\,\,\, , \,\,\,\, x \gt 0 \]

Possiamo considerare questa funzione come funzione inversa della potenza n-esima, e possiamo scrivere: \[ y = \sqrt[n]{x} \Leftrightarrow x = y^n \]

Quindi, se vogliamo calcolare la derivata della funzione radice n- esima, possiamo applicare la formula vista precedentemente: \[ y’ = \frac{1}{D(y^n)} \]

Svolgiamo ora i calcoli, e determiniamo la derivata della funzione $ y^n $: \[ y’ = \frac{1}{D(y^n)} = \frac{1}{n \cdot y^{n-1}} \]

Sapendo che le funzioni sono una l’inversa dell’altra, abbiamo la seguente uguaglianza: \[ y’ = \frac{1}{n \cdot y^{n-1}} = \frac{1}{n \cdot (\sqrt[n]{x})^{n-1}}  = \frac{1}{n \cdot \sqrt[n]{x^{n-1}}} \]

Che corrisponde proprio alla formula che utilizziamo per calcolare la derivata della funzione radice n-esima.

• Consideriamo ora la funzione esponenziale di equazione: \[ y = a^x \,\,\,\, , \,\,\,\, x \in \mathbb{R} \,\,\,\, , \,\,\,\, a \gt 0 \]

Come sappiamo, la funzione inversa dell’esponenziale è la funzione logaritmica, infatti abbiamo la seguente relazione: \[ y = a^x \Leftrightarrow x = \log_a y \]

Anche in questo caso, possiamo calcolare la derivate della funzione esponenziale utilizzando la formula vista in precedenza: \[ y’ = \frac{1}{D(\log_a y)} = \frac{1}{\frac{1}{y} \cdot \frac{1}{\log a}} = y \cdot \log a \]

Dalla relazione che abbiamo tra le funzioni x ed y, possiamo riscrivere la derivata in questo modo: \[ y’ = a^x \cdot \log a \]

Derivate delle inverse delle funzioni goniometriche

Così come per le funzioni viste in precedenza, anche nel caso delle funzioni goniometriche possiamo calcolare le derivate delle inverse.

Derivata della funzione inversa del seno

La funzione inversa del seno è la funzione arcoseno, che è espressa dalla seguente equazione: \( y = \arcsin x \). La derivata di questa funzione può essere calcolate con la seguente formula: \[ y = \arcsin x \Rightarrow y’ = \frac{1}{\sqrt{1 – x^2}} \]

Derivata della funzione inversa del coseno

La funzione inversa del coseno è la funzione arcocoseno, che ha equazione: \( y = \arccos x \). La derivata di questa funzione può essere calcolata con la seguente formula: \[ y = \arccos x \Rightarrow y’ = -\frac{1}{\sqrt{1-x^2}} \]

Derivata della funzione inversa della tangente

La funzione inversa della tangente è la funzione arcotangente, con equazione: \( y = arctan x \). La derivata di questa funzione può essere calcolate con la seguente formula: \[ y = \arctan x \Rightarrow y’ = \frac{1}{1+x^2} \]

Derivata della funzione inversa della cotangente

La funzione inversa della cotangente è la funzione arcocotangente, con equazione: \(\def\arccot{\mbox{arccot}} y = \arccot x \). La derivata di questa funzione può essere calcolate con la seguente formula: \[ y = \arccot x \Rightarrow y’ = -\frac{1}{1+x^2} \]

Notiamo che, mentre le derivate delle inverse della tangente e della cotangente sono definite per ogni x reale, le derivate delle inverse di seno e coseno non sono definite per x = 1 e x = -1, anche se per questi valori sono definite le funzioni di partenza. in questo caso, quindi, i domini delle funzioni di partenza e di quelle derivate non coincidono.

Esempio: Calcoliamo la derivata della seguente funzione composta: \[ y = \arctan(\sqrt{x}) \]

Come sappiamo, per calcolare la derivata di una funzione composta, espressa come \( f(x) \circ g(x) \), dobbiamo calcolare il prodotto tra la derivata della funzione stessa \( (f’(g(x)) \) per la derivata della funzione \( g’(x) \). In questo caso, abbiamo quindi: \[ y’ = D\Big[ \arctan(\sqrt{x}) \Big] \cdot D(\sqrt{x}) \]

Calcoliamo quindi le derivate, e svolgiamo i calcoli: \[ y’ = \frac{1}{1+(\sqrt{x})^2} \cdot \frac{1}{2\sqrt{x}} = \frac{1}{1+x} \cdot \frac{1}{2\sqrt{x}}= \frac{1}{2(1+x)\sqrt{x}} \]

Molto spesso, le funzioni con cui abbiamo a che fare sono formate dalla composizioni di funzioni che possono esser ricondotte alle elementari.

Per esempio, consideriamo due funzioni f(x) e g(x); la funzione composta, che chiamiamo h(x), è data da \( f(x) \circ g(x) \), che si può anche scrivere come $ h(x) = f(g(x)) $. In questo caso, se vogliamo calcolare la derivata di funzione composta, cioè $ h’(x) $, sappiamo che questa è data dal prodotto della derivata di g(x) per la derivata della funzione $ f(g(x)) $, cioè:

\[ \color{red}{\boxed{\color{black}{y = f(g(x)) \Rightarrow y’ = g'(x) \cdot f'(g(x))}}} \]

Esempio: Consideriamo la seguente funzione: \[ y = (2x^2 – 3x + 1)^3 \]

Possiamo considerare la funzione come composizione di due funzioni, che chiamiamo f(x) e g(x), che sono le seguenti:

\[ f(x) = x^3\,\,\,\,\,\, , \,\,\,\,\, g(x) = 2x^2 – 3x + 1 \]

Sapendo che la derivata di f(x) è $ f’(x) = 3x^2 $, possiamo facilmente calcolare la derivata della funzione $ f(g(x)) $, che è la seguente:

\( f'(g(x)) = 3 \cdot (2x^2 – 3x + 1)^2 \cdot (4x – 3) \)

Inoltre, conosciamo la derivata di g(x), che è un polinomio di secondo grado:

\( g'(x) = 2 \cdot 2x – 3 = 4x – 3 \)

Quindi, per calcolare la derivata della funzione composta, applicando la regola vista precedentemente abbiamo:

\( y’ = 3 \cdot (4x-3)(2x^2 – 3x + 1)^2 \)

Esaminiamo, ora, una particolare funzione composta, di equazione \( y = \log(f(x)) \), con \( f(x) \gt 0 \). Come abbiamo visto in precedenza, la derivata di questa funzione si può calcolare in questo modo:

\[ \color{red}{\boxed{\color{black}{y = \log[f(x)] \Rightarrow y’  = \frac{1}{f(x)} \cdot f'(x) = \frac{f'(x)}{f(x)}}}} \]

Derivate fondamentali

Con le nozioni finora acquisite, siamo in grado di determinare le derivate di altre funzioni, che possiamo assumere come derivate fondamentali.

• Consideriamo la seguente funzione: \[ y = x^\alpha \,\,\,\, , \,\,\,\, x \gt 0 \,\,\,\, , \,\,\,\, \alpha \in \mathbb{R} \]

Anche in questo caso, vale la regola che abbiamo visto nel caso in cui l’esponente è intero e positivo, quindi la derivata della funzione potenza con esponente reale è data da:

\[ y = x^\alpha \Rightarrow y’ = \alpha \cdot x^{\alpha – 1} \]

La regola vale anche nel caso in cui l’esponente sia frazionario, per esempio se abbiamo come esponente

\[ \alpha = \frac{1}{n} \]

con n intero e positivo; in questo caso, infatti, se x è elevato ad un esponente frazionario, è come se venisse applicata ad x una radice ennesima, infatti:

\[ x^{\frac{1}{n}} = \sqrt[n]{x} \]

Per calcolare la derivata di una radice ennesima, applichiamo la seguente formula:

\[ \color{red}{\boxed{\color{black}{y = \sqrt[n]{x} \Rightarrow y’=\frac{1}{n \cdot \sqrt[n]{x^{n-1}}} }}} \]

Esempio: Calcoliamo la derivata della seguente funzione: \[ y = \sqrt[3]{x} + \sqrt[5]{x} – \sqrt{x} \]

Questa funzione è composta dalla somma di tre radici di x, che sono tutte funzioni derivabili; la sua derivata, pertanto, equivale alla somma delle derivate delle singole funzioni. Applicando la formula vista in precedenza, abbiamo:

\( y’ = \frac{1}{3\sqrt[3]{x^{3-1}}} + \frac{1}{5\sqrt[5]{x^{5-1}}} – \frac{1}{2\sqrt{x^{2-1}}} = \frac{1}{3\sqrt[3]{x^2}} + \frac{1}{5\sqrt[5]{x^4}} – \frac{1}{2\sqrt{x}} \)

Possiamo calcolare la derivata della funzione precedente anche seguendo la regola vista per le funzioni potenza; sappiamo, infatti, che ogni radice può essere espressa come potenza, quindi possiamo scrivere la funzione precedente in questo modo:

\( y = x^{\frac{1}{3}} + x^{\frac{1}{5}} – x^{\frac{1}{2}} \)

Applicando, poi, la regola di derivazione per le potenze, otteniamo:

\( y’ = \frac{1}{3} x^{\frac{1}{3}-1} + \frac{1}{5} x^{\frac{1}{5}-1} – \frac{1}{2} x^{\frac{1}{2}-1} = \frac{1}{3} x^{-\frac{2}{3}} + \frac{1}{5} x^{-\frac{4}{5}} – \frac{1}{2} x^{-\frac{1}{2}} \)

Possiamo ritrasformare le potenze in radici, poiché esse hanno esponente frazionario; inoltre, poiché gli esponenti sono negativi, sappiamo che x si troverà al denominatore delle frazioni:

\( y’ = \frac{1}{3} \cdot \frac{1}{x^{\frac{2}{3}}} + \frac{1}{5} \cdot \frac{1}{x^{\frac{4}{5}}} – \frac{1}{2} \cdot \frac{1}{x^{\frac{1}{2}}} = \frac{1}{3} \cdot \frac{1}{\sqrt[3]{x^3}} + \frac{1}{5} \cdot \frac{1}{\sqrt[5]{x^4}} – \frac{1}{2} \cdot \frac{1}{\sqrt{x}} \)

la funzione derivata ottenuta, quindi, è uguale alla precedente, calcolata con la formula:

\( y’ = \frac{1}{3\sqrt[3]{x^2}} + \frac{1}{5\sqrt[5]{x^4}} – \frac{1}{2\sqrt{x}} \)

• Consideriamo, ora, la seguente funzione: \[ y = [f(x)]^{g(x)} \]

sapendo che f(x) deve essere maggiore di zero. Per calcolare la derivata della funzione possiamo applicare la seguente formula:

\[ y= [f(x)]^{g(x)} \Rightarrow y’ = [f(x)]^{g(x)} \cdot \Big\{\Big[ g'(x) \log f(x) + g(x) \frac{f'(x)}{f(x)} \Big]\Big\} \]

Esempio: Consideriamo la seguente funzione, e calcoliamo la sua derivata:

\( y = x^{2x} \)

possiamo calcolarne la derivata applicando la formula vista precedentemente, cioè:

\( y’ = x^{2x} \cdot \Big\{\Big[D(2x) \cdot \log x + 2x \cdot \frac{D(x)}{x}\Big]\Big\} \)

Calcoliamo le derivare delle funzioni che compaiono, e svolgiamo i conti:

\( y’ = x^{2x} \cdot \Big\{\Big[ 2 \log x + 2x \cdot \frac{1}{x} \Big]\Big\} = x^{2x} \cdot (2 \log x + 2) = 2x^{2x} \cdot (\log x + 1) \)

Per avere una conferma, possiamo calcolare la derivata con un metodo alternativo; sappiamo che le funzioni di questo tipo possono essere espresse come potenze con base e, quindi, la nostra funzione può essere scritta in questo modo:

\( y = x^{2x} = e^{2x \cdot \log x} \)

Possiamo, poi, calcolare questa derivata come derivate di due funzioni composte, una delle quali è $e^x$, e l’altra è \( 2x\log(x) \), quindi:

\( y’ = D(e^{2x\cdot \log x}) \cdot D(2x \cdot \log x) \)

Calcoliamo le derivate delle funzioni:

\( y’ = e^{2x \cdot \log x} \cdot \Big(2\log x + 2x \cdot \frac{1}{x}\Big) = \)

\( = e^{2x \cdot \log x} \cdot (2 \log x + 2) = 2x^{2x} \cdot (\log x + 1) \)

Teorema: La derivata della somma di due funzioni derivabili è uguale alla somma delle derivate delle funzioni stesse; si ha quindi:

\[ y = f(x) + g(x) \Rightarrow y’ = f'(x) + g'(x) \]

Un teorema molto simile si ha per la differenza di due funzioni derivabili, ed è il seguente:

Teorema: La derivata della differenza tra due funzioni derivabili è uguale alla differenza tra le derivate delle due funzioni, cioè:

\[ y = f(x) – g(x) \Rightarrow y’ = f'(x) – g'(x) \]

In generale, possiamo quindi dire che la derivata della somma algebrica di due o più funzioni derivabili è uguale alla somma algebrica delle derivate delle due funzioni.

Esempio: Consideriamo la seguente funzione, e calcoliamo la sua derivata:

\[ f(x) = \cos x + x – \log x + 3 \]

Questa funzione è costituita dalla somma algebrica di quattro funzioni; come abbiamo visto in precedenza, la sua derivata è data dalla somma algebrica delle derivate delle singole funzioni, quindi abbiamo che:

\[ f'(x) = -\sin x + 1 – \frac{1}{x} \]

Teorema: La derivata del prodotto di due funzioni derivabili è uguale al prodotto della derivata della prima funzione per la seconda funzione non derivata, più il prodotto della prima funzione (non derivata) per la derivata della seconda:

\[ y = f(x) \cdot g(x) \Rightarrow y’ = f'(x) \cdot g(x) + f(x) \cdot g'(x) \]

In particolare, se una delle due funzioni è la funzione costante, allora la derivata del prodotto delle due funzioni è uguale al prodotto della funzione costante per la derivata dell’altra funzione (infatti, sappiamo che la derivata di una funzione costante è sempre uguale a zero):

\[ y = f(x) \cdot c \Rightarrow y’ = f'(x) \cdot c \]

Questa regola, che riguarda il prodotto di due funzioni, può essere estesa al prodotto di più funzioni; quindi, possiamo dire che, in generale, la derivate del prodotto di più funzioni derivabili è uguale alla somma dei prodotti della derivata di ciascuna funzione per tutte le altre non derivate.

Esempio: Calcoliamo la derivata del prodotto delle funzioni seguenti:

\[ f(x) = \sin x \,\,\,\, , \,\,\,\, g(x) = \cos x \]

Sapendo che, la derivata di sinx è cosx e che la derivata di cosx è – sinx, possiamo calcolare la derivata della funzione prodotto:

\[ y = \sin x \cdot \cos x \Rightarrow y’ = \cos x \cdot \cos x + \sin x \cdot (-\sin x) \]

Quindi, svolgendo i calcoli, otteniamo:

\[ y’ = \cos^2 x – \sin^2 x \]

Teorema: La derivate del quoziente di due funzioni derivabili (la funzione che è al denominatore deve essere diversa da zero nei punti in cui si calcola la derivata) è uguale ad una funzione che ha per denominatore il quadrato della funzione divisore, e al numeratore il prodotto tra la derivata del dividendo e il divisore, diminuito del prodotto tra il dividendo per la derivata del divisore, cioè:

\[ y = \frac{f(x)}{g(x)} \Rightarrow y’ = \frac{f'(x)\cdot g(x) – f(x) g'(x)}{[g(x)]^2} \]

In particolare, se la funzione ha per numeratore 1, allora la sua derivata ha per denominatore il quadrato del divisore, e per numeratore la derivata del divisore con segno cambiato, perché, infatti, la derivata di 1 è uguale a zero:

\[ y = \frac{1}{g(x)} \Rightarrow y’ = \frac{-g'(x)}{[g(x)]^2} \]

Esempio: Consideriamo la seguente funzione, e calcoliamo la sua derivata:

\[ y = \frac{2x-1}{x^2+1} \]

Sappiamo che la derivata del numeratore è 2, mentre la derivata del denominatore è 2x; quindi, il numeratore è dato dal prodotto tra 2 e $ (x^2 -1) $, diminuito del prodotto tra (2x -1) per 2x, mentre il denominatore è dato dal quadrato del divisore:

\[ y’ = \frac{2 \cdot (x^2+1) – 2x \cdot 2x}{(x^2+1)^2} \]

Svolgiamo i calcoli:

\( y’ = \frac{2 \cdot (x^2+1) – (2x-1) \cdot 2x}{(x^2+1)^2} = \frac{2x^2+2-4x^2+2x}{(x^2+1)^2} = \frac{2+2x-2x^2}{(x^2+1)^2} \)

Applicando i teoremi che abbiamo visto in precedenza, possiamo ricavare le derivate di altre funzioni.

Per esempio, sapendo che la tangente è data dal rapporto tra il seno e il coseno di un angolo, e conoscendo le derivate di questi, possiamo calcolare la derivata della tangente, che è data dalle seguente formula:

\[ \color{red}{\boxed{\color{blue}{y = \tan x \Rightarrow y’ = \frac{1}{\cos^2 x} = 1 + \tan^2 x}}} \]

Allo stesso modo, sapendo che la cotangente di un angolo è data dal rapporto tra il coseno e il seno di un angolo, possiamo calcolare la sua derivata, che è data da:

\[ \color{red}{\boxed{\color{blue}{y = \cot x \Rightarrow y’ = -\frac{1}{\sin^2 x} = -(1+\cot^2 x)}}} \]

In base alla definizione di derivata, è possibile calcolare le derivate di diverse funzioni; vediamo come calcolare le derivate delle funzioni elementari.

Derivata della funzione costante y = c

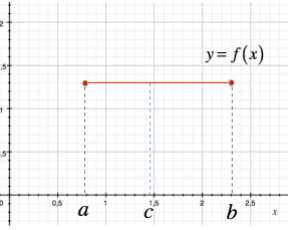
Consideriamo la funzione costante di equazione $ f(x) = c $, dove $ c $ è appunto una costante. Applicando la definizione di derivata, e calcolando il valore del rapporto incrementale, notiamo che questo è uguale a zero. Quindi, sarà zero anche il suo limite:

\[ \displaystyle \lim_{\Delta \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta \rightarrow 0} 0 = 0 \]

Quindi, possiamo affermare che la derivata della funzione costante è sempre uguale a zero:

\[ \color{red}{\boxed{\color{blue}{y = c \rightarrow y’ = 0}}} \]

In particolare, poiché la derivata di una funzione corrisponde al coefficiente angolare della tangente al grafico della funzione, possiamo affermare che il coefficiente angolare della tangente al grafico della funzione $ y = c $ in ogni suo punto è zero.

Derivata della funzione variabile indipendente y = x

Consideriamo ora la funzione $ f(x) = x $; calcolando il rapporto incrementale della funzione, ci accorgiamo che questo è uguale a 1; quindi, il limite del rapporto incrementale è dato da:

\[ \displaystyle \lim_{\Delta \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \rightarrow 0} 1 = 1 \]

Concludiamo quindi che la derivata della variabile indipendente è uguale a 1:

\[ \color{red}{\boxed{\color{blue}{y = x \rightarrow y’ = 1}}} \]

Ciò significa che il coefficiente angolare della tangente alla retta di equazione $ y = x $, cioè alla bisettrice del primo e del terzo quadrante, è uguale a 1.

Derivata della funzione potenza n-esima $ y = x^n $

Applichiamo lo stesso ragionamento per la funzione esponenziale, $ y = f(x) = x^n $, con $ n $ intero e positivo. In questo caso, il rapporto incrementale della funzione è dato da:

\( \frac{\Delta y}{\Delta x} = \frac{f(x+h)-f(x)}{h} = \frac{(x+h)^n-x^n}{h} \)

Svolgendo i calcoli, abbiamo:

\( \frac{\Delta y}{\Delta x} = \frac{x^n+nx^{n-1}+h+\ldots + m_{n-1}xh^{n-1}+h^n-x^n}{h} = nx^{n-1} + \ldots+m_{n-1}xh^{n-2}+h^{n-1} \)

Quindi, calcolando il limite per h che tende a zero, abbiamo che:

\( \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \rightarrow 0} (nx^{n-1}+\ldots+m_{n-1}xh^{n-2}+h^{n-1}) = nx^{n-1} \)

Generalizzando, possiamo affermare che la derivata della funzione potenza n-esima, e quindi il coefficiente angolare delle tangenti alle funzioni di equazioni $ y = x^n $, è data da:

\[ \color{red}{\boxed{\color{blue}{y=x^n \rightarrow y’=nx^{n-1}\,\,\, , \,\,\, n \in \mathbb{N_0}}}} \]

Derivata della funzione radice quadrata $ y = \sqrt{x} $

Consideriamo la funzione radice quadrata, $ y = f(x) = \sqrt{x} $; calcoliamo il suo rapporto incrementale:

\( \frac{\Delta y}{\Delta x} = \frac{f(x+h)-f(x)}{h} = \frac{\sqrt{x+h}-\sqrt{x}}{h} \)

Razionalizzando, e svolgendo i calcoli, otteniamo:

\( \frac{\Delta y}{\Delta x} = \frac{1}{\sqrt{x+h}+\sqrt{x}} \)

Calcoliamo, ora, il limite del rapporto incrementale per h che tende a zero:

\( \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{h \rightarrow 0} \frac{1}{\sqrt{x+h}+\sqrt{x}} = \frac{1}{2\sqrt{x}} \)

Quindi, possiamo riassumere affermando che la derivata della funzione radice quadrata, che corrisponde al coefficiente angolare della tangente al grafico di equazione $ y = \sqrt{x} \), è data da:

\[ \color{red}{\boxed{\color{blue}{y=\sqrt{x} \rightarrow y’=\frac{1}{2\sqrt{x}}}}} \]

Derivata delle funzioni \( y = \sin x \) e \( y = \cos x \)

Calcoliamo il rapporto incrementale della funzione \( y = f(x) = \sin x \):

\( \frac{\Delta y}{\Delta x} = \frac{f(x+h)-f(x)}{h} = \frac{\sin(x+h)-\sin(x)}{h} \)

applicando al numeratore una delle formule di prostaferesi, otteniamo che:

\( \frac{\Delta y}{\Delta x} = \frac{\sin \frac{h}{2}}{\frac{h}{2}} \cdot \cos\Big( x + \frac{h}{2}\Big) \)

Se calcoliamo ora il limite del rapporto incrementale per h che tende a zero, otteniamo \( \cos x \), in quanto il primo fattore del rapporto incrementale può essere ricondotto al limite notevole \( sinx/x \):

\( \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{h \rightarrow 0} \frac{\sin \frac{h}{2}}{\frac{h}{2}} \cdot \cos \Big( x + \frac{h}{2} \Big) = \cos x \)

Concludiamo, quindi, che la derivata di \( \sin x \) è \( \cos x \):

\[ \color{red}{\boxed{\color{blue}{y = \sin x \rightarrow y’ = \cos x}}} \]

Con ragionamenti analoghi, e seguendo lo stesso procedimento, possiamo calcolare la derivata della funzione \( y = \cos x \), che vale \( -\sin x \):

\[ \color{red}{\boxed{\color{blue}{y = \cos x \rightarrow y’ = -\sin x}}} \]

Derivata della funzione logaritmica

Consideriamo la seguente funzione logaritmica:

\( y = f(x) = \log_a x \,\,\,\, , \,\,\,\, a \in \mathbb{R^{+}} – \{1\} \)

Anche in questo caso, calcoliamo il valore del rapporto incrementale:

\( \frac{\Delta y}{\Delta x} = \frac{f(x+h)-f(x)}{h} = \frac{\log_a(x+h)-\log_a(x)}{h} \)

Sfruttando le proprietà dei logaritmi, la scrittura precedente può essere trasformata nella seguente:

\( \frac{\Delta y}{\Delta x} = \frac{1}{x} \log_a \Big( 1 + \frac{h}{x}\Big)^{\frac{x}{h}} \)

Volendo calcolare il suo limite per h che tende a zero, dobbiamo effettuare un cambio di incognita, ponendo $ z = x/h $, quindi:

\( \frac{\Delta y}{\Delta x} = \frac{1}{x} \log_a \Big( 1 + \frac{1}{z} \Big)^z \)

Calcolando il suo limite, per z che tende a infinito, abbiamo che:

\( \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{z \rightarrow \infty} \frac{1}{x} \log_a \Big( 1 + \frac{1}{z} \Big)^z = \frac{1}{x} \log_a e \)

Riassumendo, la derivata della funzione logaritmica, e quindi il coefficiente angolare della retta ad essa tangente, è data da:

\[ \color{red}{\boxed{\color{blue}{y = \log_a x \rightarrow y’ = \frac{1}{x} \log_a e = \frac{1}{x \cdot \log a} }}} \]

In particolare, se $a = e$, abbiamo:

\[ \color{red}{\boxed{\color{blue}{y = \log x \rightarrow y’ = \frac{1}{x}}}} \]

Derivata della funzione esponenziale $y = a^x$

Consideriamo la funzione esponenziale $ y = a^x $, con $ a $ positivo, e calcoliamo il suo rapporto incrementale:

\( \frac{\Delta y}{\Delta x} = \frac{f(x+h)-f(x)}{h} =\frac{a^{x+h}-a^x}{h} \)

Calcolando il limite per h che tende a zero, abbiamo che:

\( \displaystyle \lim_{\Delta \rightarrow 0} \frac{\Delta y}{\Delta x} =\lim_{h \rightarrow 0} \frac{a^{x+h}-a^x}{h} = \lim_{h \rightarrow 0} \frac{a^x (a^h-1)}{h} = a^x \cdot \log a \)

Quindi, possiamo riassumere affermando che la derivata della funzione esponenziale, e quindi il coefficiente angolare della retta ad essa tangente, è data da:

\[ \color{red}{\boxed{\color{blue}{y = a^x \rightarrow y’ = a^x \cdot \log a}}} \]

In particolare, se $ a = e $, abbiamo:

\[ \color{red}{\boxed{\color{blue}{y=e^x \rightarrow y’=e^x}}} \]

Tabella delle derivate elementari

\[ \color{red}{\boxed{\color{blue}{y = c \rightarrow y’ = 0}}}\]

\[ \color{red}{\boxed{\color{blue}{y = x \rightarrow y’ = 1}}}\]

\[ \color{red}{\boxed{\color{blue}{y = x^n \rightarrow  y’ = nx^{n-1} \,\,\,\, , \,\,\,\, n \in \mathbb{N_0}}}}\]

\[ \color{red}{\boxed{\color{blue}{y = \sqrt{x} \rightarrow y’ = \frac{1}{2\sqrt{x}}}}}\]

\[ \color{red}{\boxed{\color{blue}{y = \sin x \rightarrow y’ = \cos x}}}\]

\[ \color{red}{\boxed{\color{blue}{y = \cos x \rightarrow y’ = -\sin x}}}\]

\[ \color{red}{\boxed{\color{blue}{y = \log_a x \rightarrow y’ = \frac{1}{x} \log_a e = \frac{1}{x \cdot \log a} }}}\]

\[ \color{red}{\boxed{\color{blue}{y = \log x \rightarrow y’ = \frac{1}{x}}}}\]

\[ \color{red}{\boxed{\color{blue}{y = a^x \rightarrow y’ = a^x \cdot \log a}}}\]

\[ \color{red}{\boxed{\color{blue}{y = e^x \rightarrow y’ = e^x}}}\]

Teorema: Ogni funzione, che ammette derivata finita in un punto, è continua in quel punto.

Il teorema non è invertibile, cioè non è detto che una funzione che è continua in un punto sia anche derivabile in quel punto. Infatti, esistono delle funzioni per cui, in determinati punti, al tendere di h (incremento) il rapporto incrementale o non ammette limite, o tende all’infinito.

Possiamo quindi affermare che la continuità di una funzione è condizione necessaria, ma non sufficiente per la sua derivabilità.

Esempio di funzione continua ma non derivabile

Consideriamo la seguente funzione: \[ y = f(x) = |x| \]

Analizziamo il suo comportamento nel punto x = 0. La funzione è continua in x = 0, in quanto è definita in tale punto: \[ f(0) = |0| = 0 \]

Esiste il limite della funzione per \( x \rightarrow 0 \), in quanto esistono i limiti destri e sinistri per \( x \rightarrow 0 \):

\( \lim_{x \rightarrow 0^{+}} f(x) = \lim_{x \rightarrow 0^{+}} |x| = \lim_{x \rightarrow 0^{+}} x = 0 \)

\( \lim_{x \rightarrow 0^{-}} f(x) = \lim_{x \rightarrow 0^{-}} |x| = \lim_{x \rightarrow 0^{-}} -x = 0 \)

da cui segue

\( \lim_{x \rightarrow 0} f(x) = 0 \)

Il limite per \( x \rightarrow 0 \) coincide proprio con il valore che la funzione assume nel punto x = 0:

\[ \lim_{x \rightarrow 0} f(x) = f(0) = 0 \]

Affinché la funzione sia anche derivabile in x = 0 è necessario che esista il limite del rapporto incrementale per \( h \rightarrow 0 \):

\( \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} = \lim_{h \rightarrow 0} \frac{f(0+h)-f(0)}{h} = \)

\( \lim_{h \rightarrow 0} \frac{|h|-0}{h} = \lim_{h \rightarrow 0} \frac{|h|}{h} \)
Tuttavia, tale limite non esiste, poiché il limite destro e sinistro per \( h \rightarrow 0 \) sono differenti:

\( \lim_{h \rightarrow 0^{+}} \frac{|h|}{h} = \lim_{h \rightarrow 0^{+}} \frac{h}{h} = 1 \)

\( \lim_{h \rightarrow 0^{-}} \frac{|h|}{h} = \lim_{h \rightarrow 0^{-}} \frac{-h}{h} = -1 \)

Il rapporto incrementale di una funzione f(x) calcolato nel punto x0, relativamente ad un incremento h, corrisponde al coefficiente angolare della retta secante il grafico di y = f(x) nei suoi punti P e Q di ascisse, rispettivamente, $ x_0 $ e $x_0 + h $, ed è anche la tangente goniometrica dell’angolo che tale retta forma con il semiasse positivo delle ascisse.

Prendiamo una funzione f(x) derivabile nel punto $x_0$. Notiamo che, se facciamo tendere h a zero, cioè se attribuiamo all’incremento valori sempre più piccoli, il punto Q si avvicinerà sempre di più al punto P, quindi, la retta secante per PQ tenderà a diventare la retta tangente alla funzione nel punto P.

Quindi, il coefficiente angolare della retta per PQ, che corrisponde al rapporto incrementale seguente:

\[ m_{PQ} = \frac{f(x_o+h)-f(x_0)}{h} \]

tenderà sempre di più ad avvicinarsi al coefficiente angolare della retta tangente al grafico in P; sapendo che il limite del rapporto incrementale per \( h \rightarrow 0 \) è uguale alla derivata della funzione nel punto $ x_0 $, possiamo scrivere che:

\[ \lim_{h \rightarrow 0} \frac{}{} = f_{x_0}'(x_0) = m_1 \]

Possiamo affermare che il limite del rapporto incrementale, o la derivata di una funzione nel punto $x_0$, è il coefficiente angolare della retta tangente al grafico di y = f(x) nel punto di ascissa $ x_0 $.

O anche che, la derivata di una funzione in un suo punto $ x_0 $ è la tangente goniometrica dell’angolo formato dalla retta tangente al grafico di y = f(x) nel suo punto di ascissa $ x_0 $ con il semiasse positivo delle ascisse.

In particolare, notiamo che se la derivata in un punto è infinita, la retta tangente al grafico della funzione in quel punto formerà con l’asse delle ascisse una angolo di 90°, e sarà quindi parallela all’asse delle y.

Viceversa, se la derivata in un punto $ x_0 $ è zero, allora la retta tangente al grafico della funzione in quel punto risulterà parallela all’asse delle x; infatti, il coefficiente angolare della retta x = 0, e di tutte le rette ad essa parallele, è nullo.

Altro materiale di supporto

Videolezione: La derivata: definizione e significato geometrico

Consideriamo la funzione f(x) definita in un intorno I del punto $ x_0 $. Se incrementiamo $ x_0 $ di una quantità h, cioè abbiamo un incremento \( \Delta x = h \), positivo o negativo, tale che \( x_0 + h \in I \), la funzione f(x) assumerà in quel punto il valore \( f(x_0 + h) \).

Tale incremento della funzione viene indicato con \( \Delta y = f(x_o + h) – f(x_0) \), e può essere positivo, negativo o nullo.

Consideriamo ora il rapporto tra l’incremento della funzione e l’incremento della variabile corrispondente:

\[ \frac{\Delta y}{\Delta x} = \frac{f(x_0 + h)-f(x_0)}{h} \]

Questo rapporto viene definito rapporto incrementale della funzione f(x) relativo al punto \( x_0 \) e all’incremento h.

Rappresentiamo graficamente il concetto di rapporto incrementale.

Consideriamo, nel piano cartesiano, una curva generica f(x), e siano P e Q i punti di tale curva tali che le loro ascisse siano, rispettivamente, \( x_0 \) e \( x_0 + h \).

Sappiamo che il coefficiente angolare di una retta si può ottenere come il rapporto tra la differenza delle ordinate e la differenza delle ascisse di due qualsiasi punti della curva. Quindi, considerando la retta per P e Q, il suo coefficiente angolare è dato da:

\[ m_{PQ} = \frac{y_Q – y_P}{x_Q – x_P} = \frac{f(x_0+h)-f(x_0)}{x_0+h-x_0} = \frac{f(x_0+h)-f(x_0)}{h} \]

Quindi, possiamo affermare che il rapporto incrementale è uguale al coefficiente angolare della retta secante il grafico di y = f(x) nei suoi punti di ascissa \( x_0 \) e \( x_0 + h \).

Inoltre, consideriamo la retta per PQ e l’angolo che essa forma con il semiasse positivo delle ascisse, che chiamiamo \( \phi \).

Gli angoli \( \phi \) e QPM sono congruenti, perché angoli corrispondenti rispetto alle parallele Ox e PM con la trasversale PQ.

Ricordando le proprietà delle funzioni goniometriche, la tangente di tali angoli è data da:

\[ \tan \phi = \frac{MQ}{PM} = \frac{y_Q – y_M}{x_M – x_P} = \frac{y_Q – y_P}{x_Q – x_P} = \frac{f(x_o+h)-f(x_0)}{h} \]

Possiamo quindi concludere affermando che il rapporto incrementale è uguale alla tangente goniometrica dell’angolo formato dal semiasse positivo delle ascisse e dalla secante al grafico di y = f(x) passante per i suoi punti di ascisse \( x_0 \) e \( x_0 + h \).

La derivata

Consideriamo la funzione f(x) definita in un intorno completo di $x_0$ e consideriamo il rapporto incrementale, essendo h l’incremento. Facciamo tendere a zero l’incremento h, e consideriamo quindi il limite del rapporto incrementale, quando l’incremento tende a zero:

\[ \lim_{h \rightarrow 0} \frac{f(x_0 + h) – f(x_0)}{h} \]

Se tale limite esiste ed è finito, si dice che la funzione è derivabile nel punto $ x_0 $, e tale limite prende il nome di derivata della funzione per \( x = x_0 \).

Tale derivata si indica con \( f'(x_0) \).

Se, invece, tale limite non esiste, non esiste neanche la derivata.

Se il limite del rapporto incrementale è infinito, la funzione non è derivabile, e si dice che la derivata è infinita.

Quindi, ricapitolando, la derivata di una funzione f(x) in un punto $ x_0 $ è il limite, se esiste, del rapporto incrementale, al tendere a zero dell’incremento dato alla variabile indipendente.

Per definizione, abbiamo quindi che:

\[ \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} = f'(x_0) \]

Si dice, inoltre, che una funzione è derivabile in un intervallo (a; b) se è derivabile in ogni punto dell’intervallo (a; b). In questo caso, la derivata è definita in ogni punto \( x \in (a; b ) \), e risulta essere anch’essa una funzione di x, che viene definita funzione derivata.

Inoltre, considerando la funzione f(x) nel solo punto $ x_0 $, e in particolare in un suo intorno destro o sinistro, possiamo parlare, rispettivamente, di derivata destra o derivata sinistra, che si indicano in questo modo:

\[ \lim_{h \rightarrow 0^{+}} \frac{f(x_0+h)-f(x_0)}{h} = f_{+}'(x_0) \rightarrow \mbox{( derivata destra )}\]

\[ \lim_{h \rightarrow 0^{-}} \frac{f(x_0+h)-f(x_0)}{h} = f_{-}'(x_0) \rightarrow \mbox{( derivata sinistra )} \]

In particolare, una funzione è derivabile in un punto solo se esistono finite e sono uguali tra loro le derivate destra e sinistra in quel punto.

Se una funzione è definita in un intervallo chiuso [a; b ], diremo che, se esistono, \( f'(a) \) è la derivata destra, mentre \( f'(b) \) è la derivata sinistra. La funzione è inoltre derivabile in tutto [a; b] se è derivabile in tutti i punti interni di [a; b ] e negli estremi.

Altro materiale di supporto

Videolezione: derivata definizione e significato geometrico